Graph Persistence goes Spectral

Including intricate topological information (e.g., cycles) provably enhances the expressivity of message-passing graph neural networks (GNNs) beyond the Weisfeiler-Leman (WL) hierarchy. Consequently, Persistent Homology (PH) methods are increasingly employed for graph representation learning. In this context, recent works have proposed decorating classical PH diagrams with vertex and edge features for improved expressivity. However, due to their dependence on features, these methods still fail to capture basic graph structural information. In this paper, we propose SpectRe -- a new topological descriptor for graphs that integrates spectral information into PH diagrams. Notably, SpectRe is strictly more expressive than existing descriptors on graphs. We also introduce notions of global and local stability to analyze existing descriptors and establish that SpectRe is locally stable. Finally, experiments on synthetic and real-world datasets demonstrate the effectiveness of SpectRe and its potential to enhance the capabilities of graph models in relevant learning tasks.

Positional Encoding meets Persistent Homology on Graphs

The local inductive bias of message-passing graph neural networks (GNNs) hampers their ability to exploit key structural information (e.g., connectivity and cycles). Positional encoding (PE) and Persistent Homology (PH) have emerged as two promising approaches to mitigate this issue. PE schemes endow GNNs with location-aware features, while PH methods enhance GNNs with multiresolution topological features. However, a rigorous theoretical characterization of the relative merits and shortcomings of PE and PH has remained elusive. We bridge this gap by establishing that neither paradigm is more expressive than the other, providing novel constructions where one approach fails but the other succeeds. Our insights inform the design of a novel learnable method, PiPE (Persistence-informed Positional Encoding), which is provably more expressive than both PH and PE. PiPE demonstrates strong performance across a variety of tasks (e.g., molecule property prediction, graph classification, and out-of-distribution generalization), thereby advancing the frontiers of graph representation learning. Code is available at https://github.com/Aalto-QuML/PIPE.

Spacetime Geometry of Denoising in Diffusion Models

We present a novel perspective on diffusion models using the framework of information geometry. We show that the set of noisy samples, taken across all noise levels simultaneously, forms a statistical manifold -- a family of denoising probability distributions. Interpreting the noise level as a temporal parameter, we refer to this manifold as spacetime. This manifold naturally carries a Fisher-Rao metric, which defines geodesics -- shortest paths between noisy points. Notably, this family of distributions is exponential, enabling efficient geodesic computation even in high-dimensional settings without retraining or fine-tuning. We demonstrate the practical value of this geometric viewpoint in transition path sampling, where spacetime geodesics define smooth sequences of Boltzmann distributions, enabling the generation of continuous trajectories between low-energy metastable states. Code is available at: https://github.com/Aalto-QuML/diffusion-spacetime-geometry.

Heterophily-informed Message Passing

Graph neural networks (GNNs) are known to be vulnerable to oversmoothing due to their implicit homophily assumption. We mitigate this problem with a novel scheme that regulates the aggregation of messages, modulating the type and extent of message passing locally thereby preserving both the low and high-frequency components of information. Our approach relies solely on learnt embeddings, obviating the need for auxiliary labels, thus extending the benefits of heterophily-aware embeddings to broader applications, e.g., generative modelling. Our experiments, conducted across various data sets and GNN architectures, demonstrate performance enhancements and reveal heterophily patterns across standard classification benchmarks. Furthermore, application to molecular generation showcases notable performance improvements on chemoinformatics benchmarks.

Robust Simulation-Based Inference under Missing Data via Neural Processes

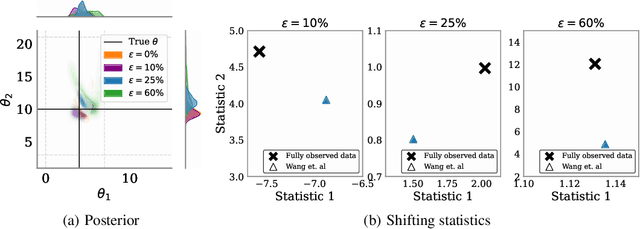
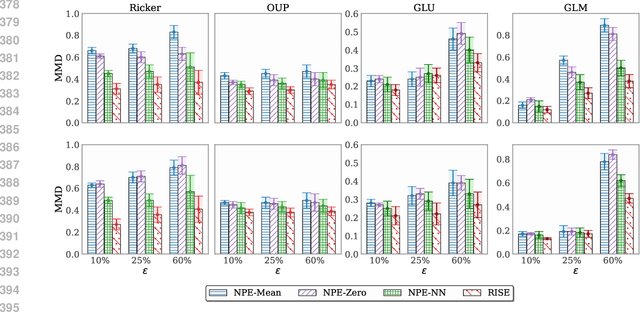
Simulation-based inference (SBI) methods typically require fully observed data to infer parameters of models with intractable likelihood functions. However, datasets often contain missing values due to incomplete observations, data corruptions (common in astrophysics), or instrument limitations (e.g., in high-energy physics applications). In such scenarios, missing data must be imputed before applying any SBI method. We formalize the problem of missing data in SBI and demonstrate that naive imputation methods can introduce bias in the estimation of SBI posterior. We also introduce a novel amortized method that addresses this issue by jointly learning the imputation model and the inference network within a neural posterior estimation (NPE) framework. Extensive empirical results on SBI benchmarks show that our approach provides robust inference outcomes compared to standard baselines for varying levels of missing data. Moreover, we demonstrate the merits of our imputation model on two real-world bioactivity datasets (Adrenergic and Kinase assays). Code is available at https://github.com/Aalto-QuML/RISE.

Devil is in the Details: Density Guidance for Detail-Aware Generation with Flow Models

Diffusion models have emerged as a powerful class of generative models, capable of producing high-quality images by mapping noise to a data distribution. However, recent findings suggest that image likelihood does not align with perceptual quality: high-likelihood samples tend to be smooth, while lower-likelihood ones are more detailed. Controlling sample density is thus crucial for balancing realism and detail. In this paper, we analyze an existing technique, Prior Guidance, which scales the latent code to influence image detail. We introduce score alignment, a condition that explains why this method works and show that it can be tractably checked for any continuous normalizing flow model. We then propose Density Guidance, a principled modification of the generative ODE that enables exact log-density control during sampling. Finally, we extend Density Guidance to stochastic sampling, ensuring precise log-density control while allowing controlled variation in structure or fine details. Our experiments demonstrate that these techniques provide fine-grained control over image detail without compromising sample quality.

Diffusion Models as Cartoonists! The Curious Case of High Density Regions

We investigate what kind of images lie in the high-density regions of diffusion models. We introduce a theoretical mode-tracking process capable of pinpointing the exact mode of the denoising distribution, and we propose a practical high-probability sampler that consistently generates images of higher likelihood than usual samplers. Our empirical findings reveal the existence of significantly higher likelihood samples that typical samplers do not produce, often manifesting as cartoon-like drawings or blurry images depending on the noise level. Curiously, these patterns emerge in datasets devoid of such examples. We also present a novel approach to track sample likelihoods in diffusion SDEs, which remarkably incurs no additional computational cost.

Diffusion Twigs with Loop Guidance for Conditional Graph Generation

We introduce a novel score-based diffusion framework named Twigs that incorporates multiple co-evolving flows for enriching conditional generation tasks. Specifically, a central or trunk diffusion process is associated with a primary variable (e.g., graph structure), and additional offshoot or stem processes are dedicated to dependent variables (e.g., graph properties or labels). A new strategy, which we call loop guidance, effectively orchestrates the flow of information between the trunk and the stem processes during sampling. This approach allows us to uncover intricate interactions and dependencies, and unlock new generative capabilities. We provide extensive experiments to demonstrate strong performance gains of the proposed method over contemporary baselines in the context of conditional graph generation, underscoring the potential of Twigs in challenging generative tasks such as inverse molecular design and molecular optimization.

ACE: Abstractions for Communicating Efficiently

A central but unresolved aspect of problem-solving in AI is the capability to introduce and use abstractions, something humans excel at. Work in cognitive science has demonstrated that humans tend towards higher levels of abstraction when engaged in collaborative task-oriented communication, enabling gradually shorter and more information-efficient utterances. Several computational methods have attempted to replicate this phenomenon, but all make unrealistic simplifying assumptions about how abstractions are introduced and learned. Our method, Abstractions for Communicating Efficiently (ACE), overcomes these limitations through a neuro-symbolic approach. On the symbolic side, we draw on work from library learning for proposing abstractions. We combine this with neural methods for communication and reinforcement learning, via a novel use of bandit algorithms for controlling the exploration and exploitation trade-off in introducing new abstractions. ACE exhibits similar tendencies to humans on a collaborative construction task from the cognitive science literature, where one agent (the architect) instructs the other (the builder) to reconstruct a scene of block-buildings. ACE results in the emergence of an efficient language as a by-product of collaborative communication. Beyond providing mechanistic insights into human communication, our work serves as a first step to providing conversational agents with the ability for human-like communicative abstractions.

What Ails Generative Structure-based Drug Design: Too Little or Too Much Expressivity?

Several generative models with elaborate training and sampling procedures have been proposed recently to accelerate structure-based drug design (SBDD); however, perplexingly, their empirical performance turns out to be suboptimal. We seek to better understand this phenomenon from both theoretical and empirical perspectives. Since most of these models apply graph neural networks (GNNs), one may suspect that they inherit the representational limitations of GNNs. We analyze this aspect, establishing the first such results for protein-ligand complexes. A plausible counterview may attribute the underperformance of these models to their excessive parameterizations, inducing expressivity at the expense of generalization. We also investigate this possibility with a simple metric-aware approach that learns an economical surrogate for affinity to infer an unlabelled molecular graph and optimizes for labels conditioned on this graph and molecular properties. The resulting model achieves state-of-the-art results using 100x fewer trainable parameters and affords up to 1000x speedup. Collectively, our findings underscore the need to reassess and redirect the existing paradigm and efforts for SBDD.