Decentralized Distributed Proximal Policy Optimization (DD-PPO) for High Performance Computing Scheduling on Multi-User Systems

Resource allocation in High Performance Computing (HPC) environments presents a complex and multifaceted challenge for job scheduling algorithms. Beyond the efficient allocation of system resources, schedulers must account for and optimize multiple performance metrics, including job wait time and system utilization. While traditional rule-based scheduling algorithms dominate the current deployments of HPC systems, the increasing heterogeneity and scale of those systems is expected to challenge the efficiency and flexibility of those algorithms in minimizing job wait time and maximizing utilization. Recent research efforts have focused on leveraging advancements in Reinforcement Learning (RL) to develop more adaptable and intelligent scheduling strategies. Recent RL-based scheduling approaches have explored a range of algorithms, from Deep Q-Networks (DQN) to Proximal Policy Optimization (PPO), and more recently, hybrid methods that integrate Graph Neural Networks with RL techniques. However, a common limitation across these methods is their reliance on relatively small datasets, and these methods face scalability issues when using large datasets. This study introduces a novel RL-based scheduler utilizing the Decentralized Distributed Proximal Policy Optimization (DD-PPO) algorithm, which supports large-scale distributed training across multiple workers without requiring parameter synchronization at every step. By eliminating reliance on centralized updates to a shared policy, the DD-PPO scheduler enhances scalability, training efficiency, and sample utilization. The validation dataset leveraged over 11.5 million real HPC job traces for comparing DD-PPO performance between traditional and advanced scheduling approaches, and the experimental results demonstrate improved scheduling performance in comparison to both rule-based schedulers and existing RL-based scheduling algorithms.

An Addendum to NeBula: Towards Extending TEAM CoSTAR's Solution to Larger Scale Environments

This paper presents an appendix to the original NeBula autonomy solution developed by the TEAM CoSTAR (Collaborative SubTerranean Autonomous Robots), participating in the DARPA Subterranean Challenge. Specifically, this paper presents extensions to NeBula's hardware, software, and algorithmic components that focus on increasing the range and scale of the exploration environment. From the algorithmic perspective, we discuss the following extensions to the original NeBula framework: (i) large-scale geometric and semantic environment mapping; (ii) an adaptive positioning system; (iii) probabilistic traversability analysis and local planning; (iv) large-scale POMDP-based global motion planning and exploration behavior; (v) large-scale networking and decentralized reasoning; (vi) communication-aware mission planning; and (vii) multi-modal ground-aerial exploration solutions. We demonstrate the application and deployment of the presented systems and solutions in various large-scale underground environments, including limestone mine exploration scenarios as well as deployment in the DARPA Subterranean challenge.

A PyTorch-Enabled Tool for Synthetic Event Camera Data Generation and Algorithm Development

Event, or neuromorphic cameras, offer a novel encoding of natural scenes by asynchronously reporting significant changes in brightness, known as events, with improved dynamic range, temporal resolution and lower data bandwidth when compared to conventional cameras. However, their adoption in domain-specific research tasks is hindered in part by limited commercial availability, lack of existing datasets, and challenges related to predicting the impact of their nonlinear optical encoding, unique noise model and tensor-based data processing requirements. To address these challenges, we introduce Synthetic Events for Neural Processing and Integration (SENPI) in Python, a PyTorch-based library for simulating and processing event camera data. SENPI includes a differentiable digital twin that converts intensity-based data into event representations, allowing for evaluation of event camera performance while handling the non-smooth and nonlinear nature of the forward model The library also supports modules for event-based I/O, manipulation, filtering and visualization, creating efficient and scalable workflows for both synthetic and real event-based data. We demonstrate SENPI's ability to produce realistic event-based data by comparing synthetic outputs to real event camera data and use these results to draw conclusions on the properties and utility of event-based perception. Additionally, we showcase SENPI's use in exploring event camera behavior under varying noise conditions and optimizing event contrast threshold for improved encoding under target conditions. Ultimately, SENPI aims to lower the barrier to entry for researchers by providing an accessible tool for event data generation and algorithmic developmnent, making it a valuable resource for advancing research in neuromorphic vision systems.

MAGIC-VFM: Meta-learning Adaptation for Ground Interaction Control with Visual Foundation Models

Control of off-road vehicles is challenging due to the complex dynamic interactions with the terrain. Accurate modeling of these interactions is important to optimize driving performance, but the relevant physical phenomena are too complex to model from first principles. Therefore, we present an offline meta-learning algorithm to construct a rapidly-tunable model of residual dynamics and disturbances. Our model processes terrain images into features using a visual foundation model (VFM), then maps these features and the vehicle state to an estimate of the current actuation matrix using a deep neural network (DNN). We then combine this model with composite adaptive control to modify the last layer of the DNN in real time, accounting for the remaining terrain interactions not captured during offline training. We provide mathematical guarantees of stability and robustness for our controller and demonstrate the effectiveness of our method through simulations and hardware experiments with a tracked vehicle and a car-like robot. We evaluate our method outdoors on different slopes with varying slippage and actuator degradation disturbances, and compare against an adaptive controller that does not use the VFM terrain features. We show significant improvement over the baseline in both hardware experimentation and simulation.

Semantics from Space: Satellite-Guided Thermal Semantic Segmentation Annotation for Aerial Field Robots

We present a new method to automatically generate semantic segmentation annotations for thermal imagery captured from an aerial vehicle by utilizing satellite-derived data products alongside onboard global positioning and attitude estimates. This new capability overcomes the challenge of developing thermal semantic perception algorithms for field robots due to the lack of annotated thermal field datasets and the time and costs of manual annotation, enabling precise and rapid annotation of thermal data from field collection efforts at a massively-parallelizable scale. By incorporating a thermal-conditioned refinement step with visual foundation models, our approach can produce highly-precise semantic segmentation labels using low-resolution satellite land cover data for little-to-no cost. It achieves 98.5% of the performance from using costly high-resolution options and demonstrates between 70-160% improvement over popular zero-shot semantic segmentation methods based on large vision-language models currently used for generating annotations for RGB imagery. Code will be available at: https://github.com/connorlee77/aerial-auto-segment.

CART: Caltech Aerial RGB-Thermal Dataset in the Wild

We present the first publicly available RGB-thermal dataset designed for aerial robotics operating in natural environments. Our dataset captures a variety of terrains across the continental United States, including rivers, lakes, coastlines, deserts, and forests, and consists of synchronized RGB, long-wave thermal, global positioning, and inertial data. Furthermore, we provide semantic segmentation annotations for 10 classes commonly encountered in natural settings in order to facilitate the development of perception algorithms robust to adverse weather and nighttime conditions. Using this dataset, we propose new and challenging benchmarks for thermal and RGB-thermal semantic segmentation, RGB-to-thermal image translation, and visual-inertial odometry. We present extensive results using state-of-the-art methods and highlight the challenges posed by temporal and geographical domain shifts in our data. Dataset and accompanying code will be provided at https://github.com/aerorobotics/caltech-aerial-rgbt-dataset

Online Self-Supervised Thermal Water Segmentation for Aerial Vehicles

We present a new method to adapt an RGB-trained water segmentation network to target-domain aerial thermal imagery using online self-supervision by leveraging texture and motion cues as supervisory signals. This new thermal capability enables current autonomous aerial robots operating in near-shore environments to perform tasks such as visual navigation, bathymetry, and flow tracking at night. Our method overcomes the problem of scarce and difficult-to-obtain near-shore thermal data that prevents the application of conventional supervised and unsupervised methods. In this work, we curate the first aerial thermal near-shore dataset, show that our approach outperforms fully-supervised segmentation models trained on limited target-domain thermal data, and demonstrate real-time capabilities onboard an Nvidia Jetson embedded computing platform. Code and datasets used in this work will be available at: https://github.com/connorlee77/uav-thermal-water-segmentation.

Efficiently-Verifiable Strong Uniquely Solvable Puzzles and Matrix Multiplication

We advance the Cohn-Umans framework for developing fast matrix multiplication algorithms. We introduce, analyze, and search for a new subclass of strong uniquely solvable puzzles (SUSP), which we call simplifiable SUSPs. We show that these puzzles are efficiently verifiable, which remains an open question for general SUSPs. We also show that individual simplifiable SUSPs can achieve the same strength of bounds on the matrix multiplication exponent $\omega$ that infinite families of SUSPs can. We report on the construction, by computer search, of larger SUSPs than previously known for small width. This, combined with our tighter analysis, strengthens the upper bound on the matrix multiplication exponent from $2.66$ to $2.505$ obtainable via this computational approach, and nears the results of the handcrafted constructions of Cohn et al.

Matrix Multiplication: Verifying Strong Uniquely Solvable Puzzles

Cohn and Umans proposed a framework for developing fast matrix multiplication algorithms based on the embedding computation in certain groups algebras. In subsequent work with Kleinberg and Szegedy, they connected this to the search for combinatorial objects called strong uniquely solvable puzzles (strong USPs). We begin a systematic computer-aided search for these objects. We develop and implement constraint-based algorithms build on reductions to $\mathrm{SAT}$ and $\mathrm{IP}$ to verify that puzzles are strong USPs, and to search for large strong USPs. We produce tight bounds on the maximum size of a strong USP for width $k \le 5$, construct puzzles of small width that are larger than previous work, and improve the upper bounds on strong USP size for $k \le 12$. Although our work only deals with puzzles of small-constant width, the strong USPs we find imply matrix multiplication algorithms that run in $O(n^\omega)$ time with exponent $\omega \le 2.66$. While our algorithms do not beat the fastest algorithms, our work provides evidence and, perhaps, a path to finding families of strong USPs that imply matrix multiplication algorithms that are more efficient than those currently known.

Neural Tree Expansion for Multi-Robot Planning in Non-Cooperative Environments

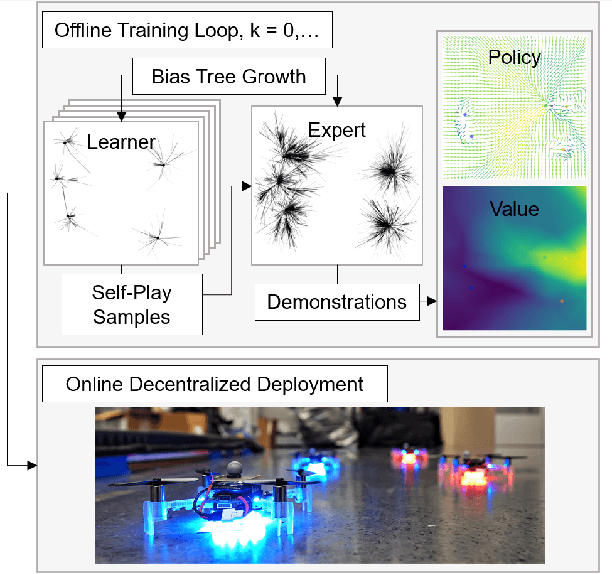
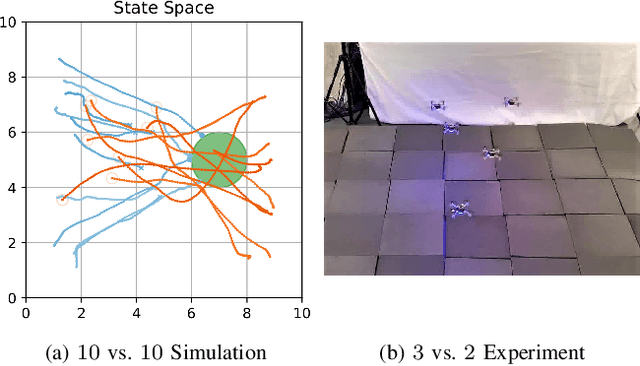
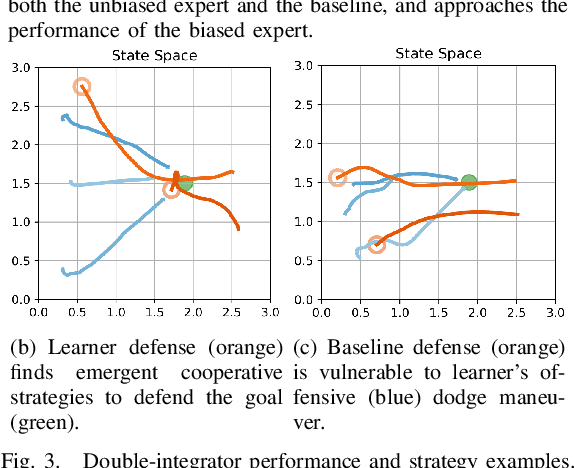
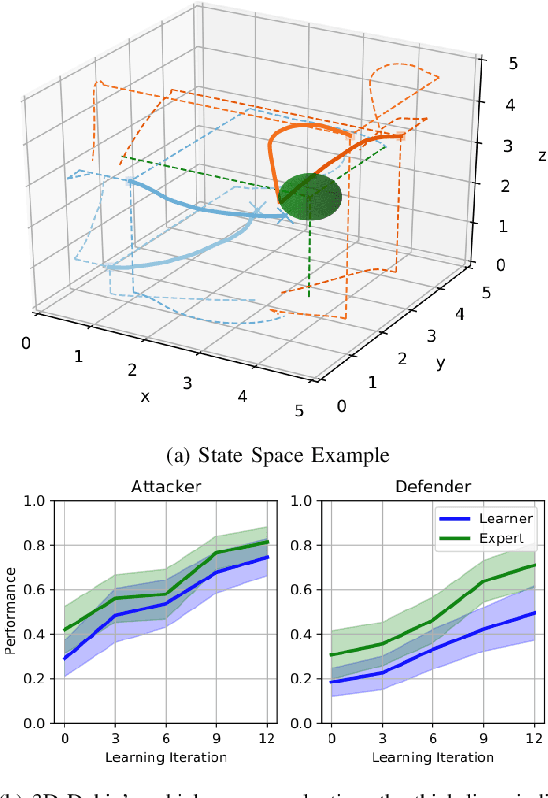
We present a self-improving, neural tree expansion method for multi-robot online planning in non-cooperative environments, where each robot tries to maximize its cumulative reward while interacting with other self-interested robots. Our algorithm adapts the centralized, perfect information, discrete-action space method from Alpha Zero to a decentralized, partial information, continuous action space setting for multi-robot applications. Our method has three interacting components: (i) a centralized, perfect-information `expert' Monte Carlo Tree Search (MCTS) with large computation resources that provides expert demonstrations, (ii) a decentralized, partial-information `learner' MCTS with small computation resources that runs in real-time and provides self-play examples, and (iii) policy & value neural networks that are trained with the expert demonstrations and bias both the expert and the learner tree growth. Our numerical experiments demonstrate neural expansion generates compact search trees with better solution quality and 20 times less computational expense compared to MCTS without neural expansion. The resulting policies are dynamically sophisticated, demonstrate coordination between robots, and play the Reach-Target-Avoid differential game significantly better than the state-of-the-art control-theoretic baseline for multi-robot, double-integrator systems. Our hardware experiments on an aerial swarm demonstrate the computational advantage of neural tree expansion, enabling online planning at 20Hz with effective policies in complex scenarios.