Lin F. Yang
Near-Optimal Reward-Free Exploration for Linear Mixture MDPs with Plug-in Solver
Oct 08, 2021Abstract:Although model-based reinforcement learning (RL) approaches are considered more sample efficient, existing algorithms are usually relying on sophisticated planning algorithm to couple tightly with the model-learning procedure. Hence the learned models may lack the ability of being re-used with more specialized planners. In this paper we address this issue and provide approaches to learn an RL model efficiently without the guidance of a reward signal. In particular, we take a plug-in solver approach, where we focus on learning a model in the exploration phase and demand that \emph{any planning algorithm} on the learned model can give a near-optimal policy. Specicially, we focus on the linear mixture MDP setting, where the probability transition matrix is a (unknown) convex combination of a set of existing models. We show that, by establishing a novel exploration algorithm, the plug-in approach learns a model by taking $\tilde{O}(d^2H^3/\epsilon^2)$ interactions with the environment and \emph{any} $\epsilon$-optimal planner on the model gives an $O(\epsilon)$-optimal policy on the original model. This sample complexity matches lower bounds for non-plug-in approaches and is \emph{statistically optimal}. We achieve this result by leveraging a careful maximum total-variance bound using Bernstein inequality and properties specified to linear mixture MDP.
Gap-Dependent Unsupervised Exploration for Reinforcement Learning
Aug 11, 2021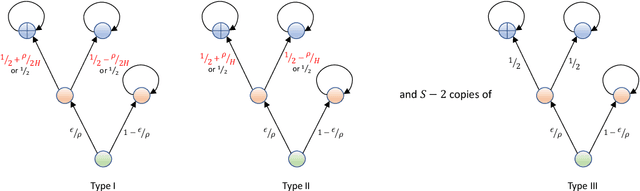
Abstract:For the problem of task-agnostic reinforcement learning (RL), an agent first collects samples from an unknown environment without the supervision of reward signals, then is revealed with a reward and is asked to compute a corresponding near-optimal policy. Existing approaches mainly concern the worst-case scenarios, in which no structural information of the reward/transition-dynamics is utilized. Therefore the best sample upper bound is $\propto\widetilde{\mathcal{O}}(1/\epsilon^2)$, where $\epsilon>0$ is the target accuracy of the obtained policy, and can be overly pessimistic. To tackle this issue, we provide an efficient algorithm that utilizes a gap parameter, $\rho>0$, to reduce the amount of exploration. In particular, for an unknown finite-horizon Markov decision process, the algorithm takes only $\widetilde{\mathcal{O}} (1/\epsilon \cdot (H^3SA / \rho + H^4 S^2 A) )$ episodes of exploration, and is able to obtain an $\epsilon$-optimal policy for a post-revealed reward with sub-optimality gap at least $\rho$, where $S$ is the number of states, $A$ is the number of actions, and $H$ is the length of the horizon, obtaining a nearly \emph{quadratic saving} in terms of $\epsilon$. We show that, information-theoretically, this bound is nearly tight for $\rho < \Theta(1/(HS))$ and $H>1$. We further show that $\propto\widetilde{\mathcal{O}}(1)$ sample bound is possible for $H=1$ (i.e., multi-armed bandit) or with a sampling simulator, establishing a stark separation between those settings and the RL setting.
Randomized Exploration for Reinforcement Learning with General Value Function Approximation
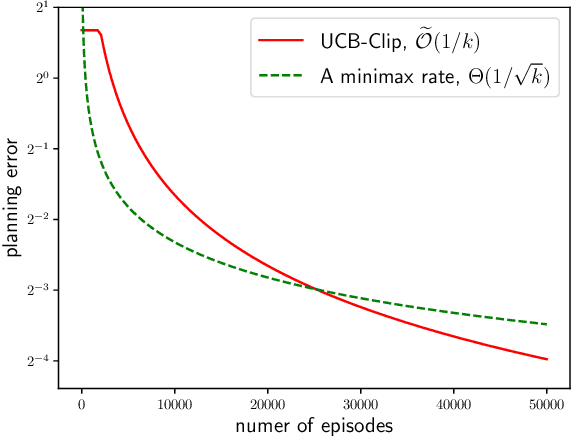
Jun 15, 2021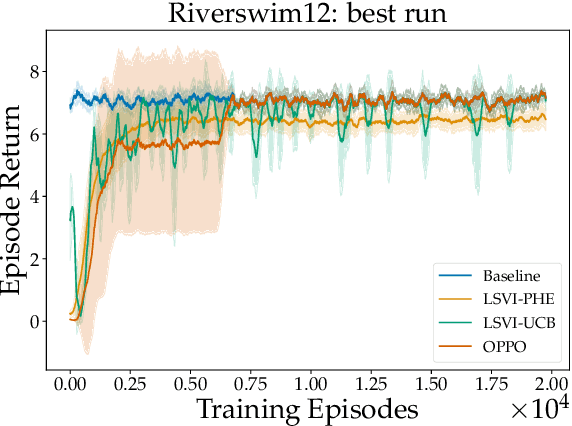
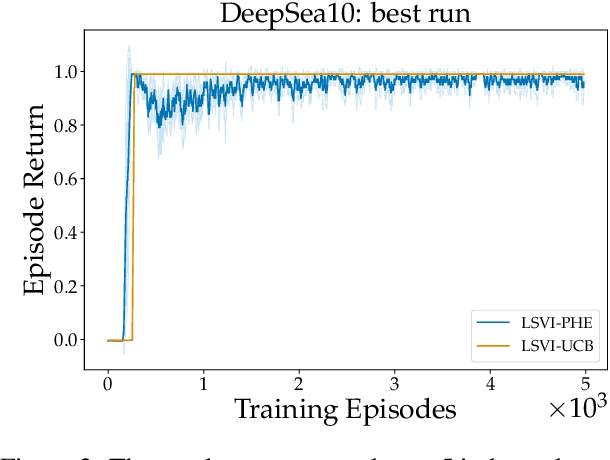
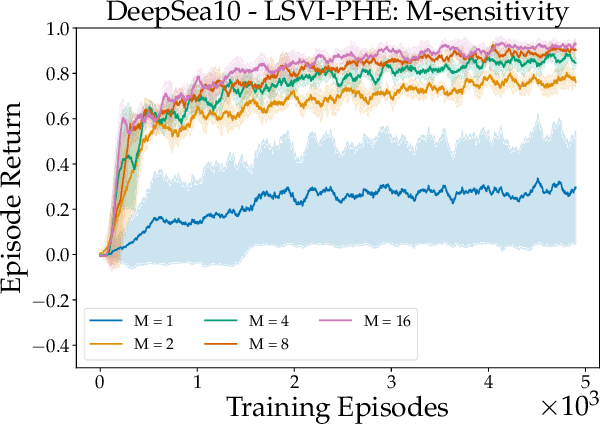
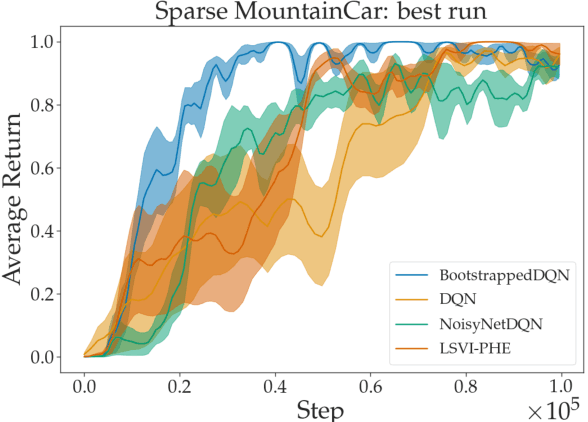
Abstract:We propose a model-free reinforcement learning algorithm inspired by the popular randomized least squares value iteration (RLSVI) algorithm as well as the optimism principle. Unlike existing upper-confidence-bound (UCB) based approaches, which are often computationally intractable, our algorithm drives exploration by simply perturbing the training data with judiciously chosen i.i.d. scalar noises. To attain optimistic value function estimation without resorting to a UCB-style bonus, we introduce an optimistic reward sampling procedure. When the value functions can be represented by a function class $\mathcal{F}$, our algorithm achieves a worst-case regret bound of $\widetilde{O}(\mathrm{poly}(d_EH)\sqrt{T})$ where $T$ is the time elapsed, $H$ is the planning horizon and $d_E$ is the $\textit{eluder dimension}$ of $\mathcal{F}$. In the linear setting, our algorithm reduces to LSVI-PHE, a variant of RLSVI, that enjoys an $\widetilde{\mathcal{O}}(\sqrt{d^3H^3T})$ regret. We complement the theory with an empirical evaluation across known difficult exploration tasks.
Online Sub-Sampling for Reinforcement Learning with General Function Approximation
Jun 14, 2021Abstract:Designing provably efficient algorithms with general function approximation is an important open problem in reinforcement learning. Recently, Wang et al.~[2020c] establish a value-based algorithm with general function approximation that enjoys $\widetilde{O}(\mathrm{poly}(dH)\sqrt{K})$\footnote{Throughout the paper, we use $\widetilde{O}(\cdot)$ to suppress logarithm factors. } regret bound, where $d$ depends on the complexity of the function class, $H$ is the planning horizon, and $K$ is the total number of episodes. However, their algorithm requires $\Omega(K)$ computation time per round, rendering the algorithm inefficient for practical use. In this paper, by applying online sub-sampling techniques, we develop an algorithm that takes $\widetilde{O}(\mathrm{poly}(dH))$ computation time per round on average, and enjoys nearly the same regret bound. Furthermore, the algorithm achieves low switching cost, i.e., it changes the policy only $\widetilde{O}(\mathrm{poly}(dH))$ times during its execution, making it appealing to be implemented in real-life scenarios. Moreover, by using an upper-confidence based exploration-driven reward function, the algorithm provably explores the environment in the reward-free setting. In particular, after $\widetilde{O}(\mathrm{poly}(dH))/\epsilon^2$ rounds of exploration, the algorithm outputs an $\epsilon$-optimal policy for any given reward function.
Safe Reinforcement Learning with Linear Function Approximation
Jun 11, 2021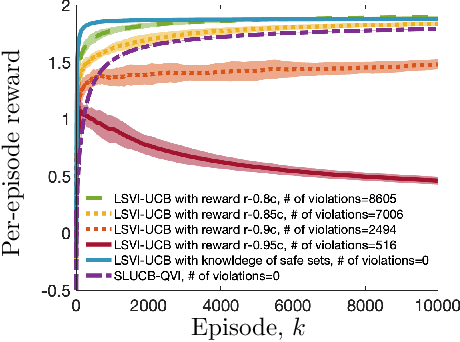
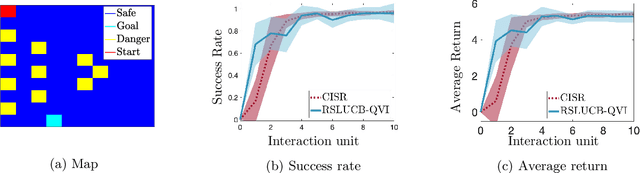
Abstract:Safety in reinforcement learning has become increasingly important in recent years. Yet, existing solutions either fail to strictly avoid choosing unsafe actions, which may lead to catastrophic results in safety-critical systems, or fail to provide regret guarantees for settings where safety constraints need to be learned. In this paper, we address both problems by first modeling safety as an unknown linear cost function of states and actions, which must always fall below a certain threshold. We then present algorithms, termed SLUCB-QVI and RSLUCB-QVI, for episodic Markov decision processes (MDPs) with linear function approximation. We show that SLUCB-QVI and RSLUCB-QVI, while with \emph{no safety violation}, achieve a $\tilde{\mathcal{O}}\left(\kappa\sqrt{d^3H^3T}\right)$ regret, nearly matching that of state-of-the-art unsafe algorithms, where $H$ is the duration of each episode, $d$ is the dimension of the feature mapping, $\kappa$ is a constant characterizing the safety constraints, and $T$ is the total number of action plays. We further present numerical simulations that corroborate our theoretical findings.
Global Neighbor Sampling for Mixed CPU-GPU Training on Giant Graphs
Jun 11, 2021


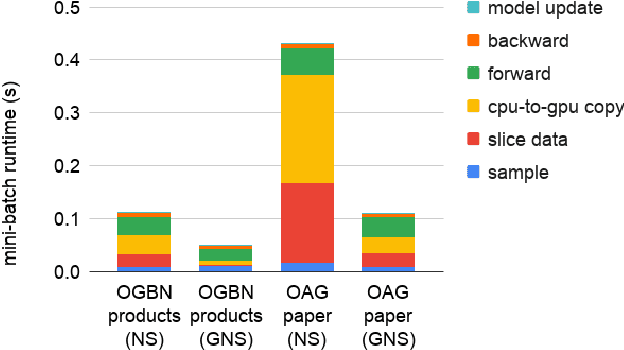
Abstract:Graph neural networks (GNNs) are powerful tools for learning from graph data and are widely used in various applications such as social network recommendation, fraud detection, and graph search. The graphs in these applications are typically large, usually containing hundreds of millions of nodes. Training GNN models on such large graphs efficiently remains a big challenge. Despite a number of sampling-based methods have been proposed to enable mini-batch training on large graphs, these methods have not been proved to work on truly industry-scale graphs, which require GPUs or mixed-CPU-GPU training. The state-of-the-art sampling-based methods are usually not optimized for these real-world hardware setups, in which data movement between CPUs and GPUs is a bottleneck. To address this issue, we propose Global Neighborhood Sampling that aims at training GNNs on giant graphs specifically for mixed-CPU-GPU training. The algorithm samples a global cache of nodes periodically for all mini-batches and stores them in GPUs. This global cache allows in-GPU importance sampling of mini-batches, which drastically reduces the number of nodes in a mini-batch, especially in the input layer, to reduce data copy between CPU and GPU and mini-batch computation without compromising the training convergence rate or model accuracy. We provide a highly efficient implementation of this method and show that our implementation outperforms an efficient node-wise neighbor sampling baseline by a factor of 2X-4X on giant graphs. It outperforms an efficient implementation of LADIES with small layers by a factor of 2X-14X while achieving much higher accuracy than LADIES.We also theoretically analyze the proposed algorithm and show that with cached node data of a proper size, it enjoys a comparable convergence rate as the underlying node-wise sampling method.
Provably Correct Optimization and Exploration with Non-linear Policies
Mar 22, 2021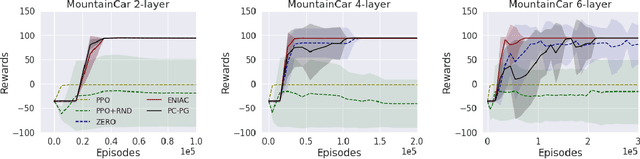
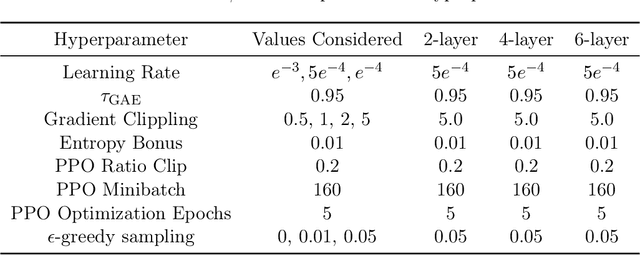
Abstract:Policy optimization methods remain a powerful workhorse in empirical Reinforcement Learning (RL), with a focus on neural policies that can easily reason over complex and continuous state and/or action spaces. Theoretical understanding of strategic exploration in policy-based methods with non-linear function approximation, however, is largely missing. In this paper, we address this question by designing ENIAC, an actor-critic method that allows non-linear function approximation in the critic. We show that under certain assumptions, e.g., a bounded eluder dimension $d$ for the critic class, the learner finds a near-optimal policy in $O(\poly(d))$ exploration rounds. The method is robust to model misspecification and strictly extends existing works on linear function approximation. We also develop some computational optimizations of our approach with slightly worse statistical guarantees and an empirical adaptation building on existing deep RL tools. We empirically evaluate this adaptation and show that it outperforms prior heuristics inspired by linear methods, establishing the value via correctly reasoning about the agent's uncertainty under non-linear function approximation.
Provably Breaking the Quadratic Error Compounding Barrier in Imitation Learning, Optimally
Feb 25, 2021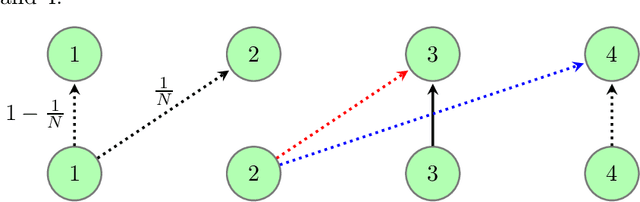
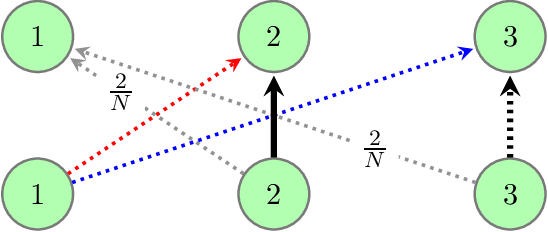
Abstract:We study the statistical limits of Imitation Learning (IL) in episodic Markov Decision Processes (MDPs) with a state space $\mathcal{S}$. We focus on the known-transition setting where the learner is provided a dataset of $N$ length-$H$ trajectories from a deterministic expert policy and knows the MDP transition. We establish an upper bound $O(|\mathcal{S}|H^{3/2}/N)$ for the suboptimality using the Mimic-MD algorithm in Rajaraman et al (2020) which we prove to be computationally efficient. In contrast, we show the minimax suboptimality grows as $\Omega( H^{3/2}/N)$ when $|\mathcal{S}|\geq 3$ while the unknown-transition setting suffers from a larger sharp rate $\Theta(|\mathcal{S}|H^2/N)$ (Rajaraman et al (2020)). The lower bound is established by proving a two-way reduction between IL and the value estimation problem of the unknown expert policy under any given reward function, as well as building connections with linear functional estimation with subsampled observations. We further show that under the additional assumption that the expert is optimal for the true reward function, there exists an efficient algorithm, which we term as Mimic-Mixture, that provably achieves suboptimality $O(1/N)$ for arbitrary 3-state MDPs with rewards only at the terminal layer. In contrast, no algorithm can achieve suboptimality $O(\sqrt{H}/N)$ with high probability if the expert is not constrained to be optimal. Our work formally establishes the benefit of the expert optimal assumption in the known transition setting, while Rajaraman et al (2020) showed it does not help when transitions are unknown.
A Provably Efficient Algorithm for Linear Markov Decision Process with Low Switching Cost
Jan 02, 2021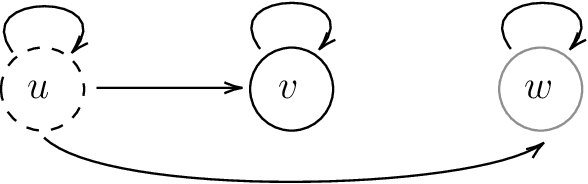
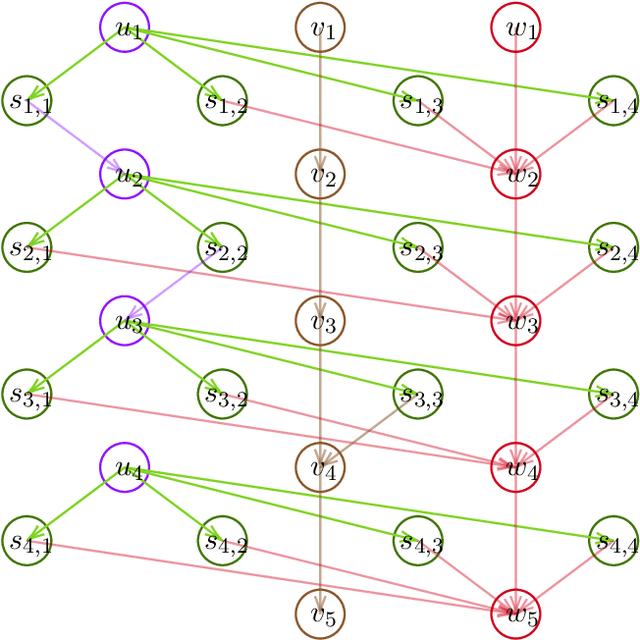
Abstract:Many real-world applications, such as those in medical domains, recommendation systems, etc, can be formulated as large state space reinforcement learning problems with only a small budget of the number of policy changes, i.e., low switching cost. This paper focuses on the linear Markov Decision Process (MDP) recently studied in [Yang et al 2019, Jin et al 2020] where the linear function approximation is used for generalization on the large state space. We present the first algorithm for linear MDP with a low switching cost. Our algorithm achieves an $\widetilde{O}\left(\sqrt{d^3H^4K}\right)$ regret bound with a near-optimal $O\left(d H\log K\right)$ global switching cost where $d$ is the feature dimension, $H$ is the planning horizon and $K$ is the number of episodes the agent plays. Our regret bound matches the best existing polynomial algorithm by [Jin et al 2020] and our switching cost is exponentially smaller than theirs. When specialized to tabular MDP, our switching cost bound improves those in [Bai et al 2019, Zhang et al 20020]. We complement our positive result with an $\Omega\left(dH/\log d\right)$ global switching cost lower bound for any no-regret algorithm.
Minimax Sample Complexity for Turn-based Stochastic Game
Nov 29, 2020Abstract:The empirical success of Multi-agent reinforcement learning is encouraging, while few theoretical guarantees have been revealed. In this work, we prove that the plug-in solver approach, probably the most natural reinforcement learning algorithm, achieves minimax sample complexity for turn-based stochastic game (TBSG). Specifically, we plan in an empirical TBSG by utilizing a `simulator' that allows sampling from arbitrary state-action pair. We show that the empirical Nash equilibrium strategy is an approximate Nash equilibrium strategy in the true TBSG and give both problem-dependent and problem-independent bound. We develop absorbing TBSG and reward perturbation techniques to tackle the complex statistical dependence. The key idea is artificially introducing a suboptimality gap in TBSG and then the Nash equilibrium strategy lies in a finite set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge