Transformers on Markov Data: Constant Depth Suffices

Attention-based transformers have been remarkably successful at modeling generative processes across various domains and modalities. In this paper, we study the behavior of transformers on data drawn from \kth Markov processes, where the conditional distribution of the next symbol in a sequence depends on the previous $k$ symbols observed. We observe a surprising phenomenon empirically which contradicts previous findings: when trained for sufficiently long, a transformer with a fixed depth and $1$ head per layer is able to achieve low test loss on sequences drawn from \kth Markov sources, even as $k$ grows. Furthermore, this low test loss is achieved by the transformer's ability to represent and learn the in-context conditional empirical distribution. On the theoretical side, our main result is that a transformer with a single head and three layers can represent the in-context conditional empirical distribution for \kth Markov sources, concurring with our empirical observations. Along the way, we prove that \textit{attention-only} transformers with $O(\log_2(k))$ layers can represent the in-context conditional empirical distribution by composing induction heads to track the previous $k$ symbols in the sequence. These results provide more insight into our current understanding of the mechanisms by which transformers learn to capture context, by understanding their behavior on Markov sources.

Toward a Theory of Tokenization in LLMs

While there has been a large body of research attempting to circumvent tokenization for language modeling (Clark et al., 2022; Xue et al., 2022), the current consensus is that it is a necessary initial step for designing state-of-the-art performant language models. In this paper, we investigate tokenization from a theoretical point of view by studying the behavior of transformers on simple data generating processes. When trained on data drawn from certain simple $k^{\text{th}}$-order Markov processes for $k > 1$, transformers exhibit a surprising phenomenon - in the absence of tokenization, they empirically fail to learn the right distribution and predict characters according to a unigram model (Makkuva et al., 2024). With the addition of tokenization, however, we empirically observe that transformers break through this barrier and are able to model the probabilities of sequences drawn from the source near-optimally, achieving small cross-entropy loss. With this observation as starting point, we study the end-to-end cross-entropy loss achieved by transformers with and without tokenization. With the appropriate tokenization, we show that even the simplest unigram models (over tokens) learnt by transformers are able to model the probability of sequences drawn from $k^{\text{th}}$-order Markov sources near optimally. Our analysis provides a justification for the use of tokenization in practice through studying the behavior of transformers on Markovian data.

Greedy Pruning with Group Lasso Provably Generalizes for Matrix Sensing and Neural Networks with Quadratic Activations

Pruning schemes have been widely used in practice to reduce the complexity of trained models with a massive number of parameters. Several practical studies have shown that pruning an overparameterized model and fine-tuning generalizes well to new samples. Although the above pipeline, which we refer to as pruning + fine-tuning, has been extremely successful in lowering the complexity of trained models, there is very little known about the theory behind this success. In this paper we address this issue by investigating the pruning + fine-tuning framework on the overparameterized matrix sensing problem, with the ground truth denoted $U_\star \in \mathbb{R}^{d \times r}$ and the overparameterized model $U \in \mathbb{R}^{d \times k}$ with $k \gg r$. We study the approximate local minima of the empirical mean square error, augmented with a smooth version of a group Lasso regularizer, $\sum_{i=1}^k \| U e_i \|_2$ and show that pruning the low $\ell_2$-norm columns results in a solution $U_{\text{prune}}$ which has the minimum number of columns $r$, yet is close to the ground truth in training loss. Initializing the subsequent fine-tuning phase from $U_{\text{prune}}$, the resulting solution converges linearly to a generalization error of $O(\sqrt{rd/n})$ ignoring lower order terms, which is statistically optimal. While our analysis provides insights into the role of regularization in pruning, we also show that running gradient descent in the absence of regularization results in models which {are not suitable for greedy pruning}, i.e., many columns could have their $\ell_2$ norm comparable to that of the maximum. Lastly, we extend our results for the training and pruning of two-layer neural networks with quadratic activation functions. Our results provide the first rigorous insights on why greedy pruning + fine-tuning leads to smaller models which also generalize well.

Beyond UCB: Statistical Complexity and Optimal Algorithms for Non-linear Ridge Bandits

We consider the sequential decision-making problem where the mean outcome is a non-linear function of the chosen action. Compared with the linear model, two curious phenomena arise in non-linear models: first, in addition to the "learning phase" with a standard parametric rate for estimation or regret, there is an "burn-in period" with a fixed cost determined by the non-linear function; second, achieving the smallest burn-in cost requires new exploration algorithms. For a special family of non-linear functions named ridge functions in the literature, we derive upper and lower bounds on the optimal burn-in cost, and in addition, on the entire learning trajectory during the burn-in period via differential equations. In particular, a two-stage algorithm that first finds a good initial action and then treats the problem as locally linear is statistically optimal. In contrast, several classical algorithms, such as UCB and algorithms relying on regression oracles, are provably suboptimal.

Sample Efficient Deep Reinforcement Learning via Local Planning

The focus of this work is sample-efficient deep reinforcement learning (RL) with a simulator. One useful property of simulators is that it is typically easy to reset the environment to a previously observed state. We propose an algorithmic framework, named uncertainty-first local planning (UFLP), that takes advantage of this property. Concretely, in each data collection iteration, with some probability, our meta-algorithm resets the environment to an observed state which has high uncertainty, instead of sampling according to the initial-state distribution. The agent-environment interaction then proceeds as in the standard online RL setting. We demonstrate that this simple procedure can dramatically improve the sample cost of several baseline RL algorithms on difficult exploration tasks. Notably, with our framework, we can achieve super-human performance on the notoriously hard Atari game, Montezuma's Revenge, with a simple (distributional) double DQN. Our work can be seen as an efficient approximate implementation of an existing algorithm with theoretical guarantees, which offers an interpretation of the positive empirical results.

Spectral Regularization Allows Data-frugal Learning over Combinatorial Spaces

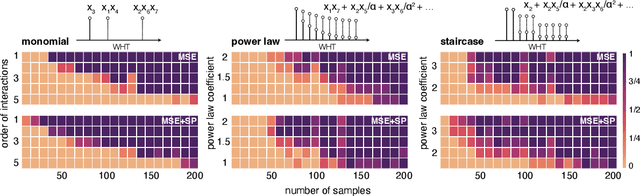
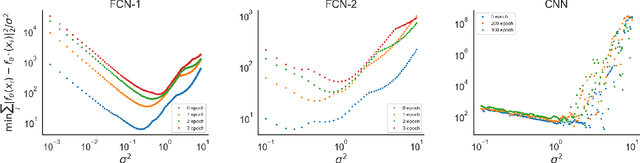
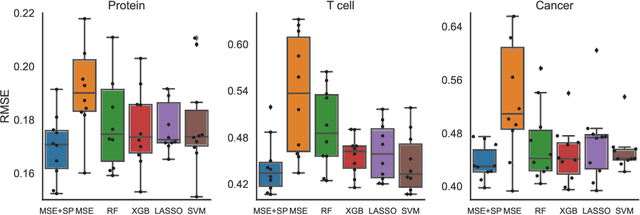
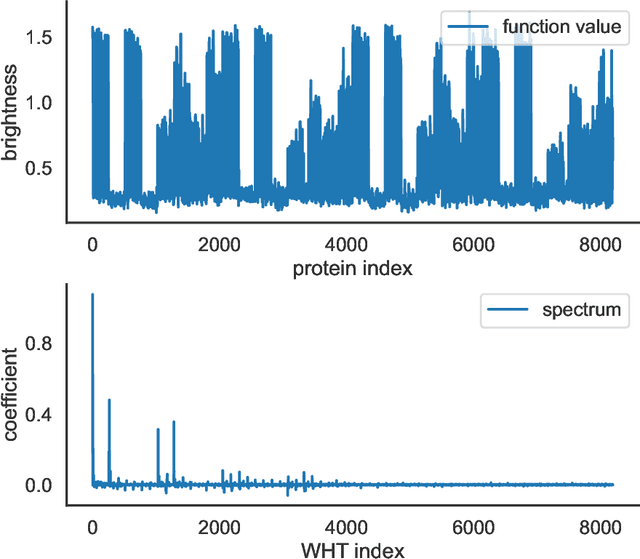
Data-driven machine learning models are being increasingly employed in several important inference problems in biology, chemistry, and physics which require learning over combinatorial spaces. Recent empirical evidence (see, e.g., [1], [2], [3]) suggests that regularizing the spectral representation of such models improves their generalization power when labeled data is scarce. However, despite these empirical studies, the theoretical underpinning of when and how spectral regularization enables improved generalization is poorly understood. In this paper, we focus on learning pseudo-Boolean functions and demonstrate that regularizing the empirical mean squared error by the L_1 norm of the spectral transform of the learned function reshapes the loss landscape and allows for data-frugal learning, under a restricted secant condition on the learner's empirical error measured against the ground truth function. Under a weaker quadratic growth condition, we show that stationary points which also approximately interpolate the training data points achieve statistically optimal generalization performance. Complementing our theory, we empirically demonstrate that running gradient descent on the regularized loss results in a better generalization performance compared to baseline algorithms in several data-scarce real-world problems.

Minimax Optimal Online Imitation Learning via Replay Estimation

Online imitation learning is the problem of how best to mimic expert demonstrations, given access to the environment or an accurate simulator. Prior work has shown that in the infinite sample regime, exact moment matching achieves value equivalence to the expert policy. However, in the finite sample regime, even if one has no optimization error, empirical variance can lead to a performance gap that scales with $H^2 / N$ for behavioral cloning and $H / \sqrt{N}$ for online moment matching, where $H$ is the horizon and $N$ is the size of the expert dataset. We introduce the technique of replay estimation to reduce this empirical variance: by repeatedly executing cached expert actions in a stochastic simulator, we compute a smoother expert visitation distribution estimate to match. In the presence of general function approximation, we prove a meta theorem reducing the performance gap of our approach to the parameter estimation error for offline classification (i.e. learning the expert policy). In the tabular setting or with linear function approximation, our meta theorem shows that the performance gap incurred by our approach achieves the optimal $\widetilde{O} \left( \min({H^{3/2}} / {N}, {H} / {\sqrt{N}} \right)$ dependency, under significantly weaker assumptions compared to prior work. We implement multiple instantiations of our approach on several continuous control tasks and find that we are able to significantly improve policy performance across a variety of dataset sizes.

Semi-supervised Active Regression

Labelled data often comes at a high cost as it may require recruiting human labelers or running costly experiments. At the same time, in many practical scenarios, one already has access to a partially labelled, potentially biased dataset that can help with the learning task at hand. Motivated by such settings, we formally initiate a study of $semi-supervised$ $active$ $learning$ through the frame of linear regression. In this setting, the learner has access to a dataset $X \in \mathbb{R}^{(n_1+n_2) \times d}$ which is composed of $n_1$ unlabelled examples that an algorithm can actively query, and $n_2$ examples labelled a-priori. Concretely, denoting the true labels by $Y \in \mathbb{R}^{n_1 + n_2}$, the learner's objective is to find $\widehat{\beta} \in \mathbb{R}^d$ such that, \begin{equation} \| X \widehat{\beta} - Y \|_2^2 \le (1 + \epsilon) \min_{\beta \in \mathbb{R}^d} \| X \beta - Y \|_2^2 \end{equation} while making as few additional label queries as possible. In order to bound the label queries, we introduce an instance dependent parameter called the reduced rank, denoted by $R_X$, and propose an efficient algorithm with query complexity $O(R_X/\epsilon)$. This result directly implies improved upper bounds for two important special cases: (i) active ridge regression, and (ii) active kernel ridge regression, where the reduced-rank equates to the statistical dimension, $sd_\lambda$ and effective dimension, $d_\lambda$ of the problem respectively, where $\lambda \ge 0$ denotes the regularization parameter. For active ridge regression we also prove a matching lower bound of $O(sd_\lambda / \epsilon)$ on the query complexity of any algorithm. This subsumes prior work that only considered the unregularized case, i.e., $\lambda = 0$.

Provably Breaking the Quadratic Error Compounding Barrier in Imitation Learning, Optimally

We study the statistical limits of Imitation Learning (IL) in episodic Markov Decision Processes (MDPs) with a state space $\mathcal{S}$. We focus on the known-transition setting where the learner is provided a dataset of $N$ length-$H$ trajectories from a deterministic expert policy and knows the MDP transition. We establish an upper bound $O(|\mathcal{S}|H^{3/2}/N)$ for the suboptimality using the Mimic-MD algorithm in Rajaraman et al (2020) which we prove to be computationally efficient. In contrast, we show the minimax suboptimality grows as $\Omega( H^{3/2}/N)$ when $|\mathcal{S}|\geq 3$ while the unknown-transition setting suffers from a larger sharp rate $\Theta(|\mathcal{S}|H^2/N)$ (Rajaraman et al (2020)). The lower bound is established by proving a two-way reduction between IL and the value estimation problem of the unknown expert policy under any given reward function, as well as building connections with linear functional estimation with subsampled observations. We further show that under the additional assumption that the expert is optimal for the true reward function, there exists an efficient algorithm, which we term as Mimic-Mixture, that provably achieves suboptimality $O(1/N)$ for arbitrary 3-state MDPs with rewards only at the terminal layer. In contrast, no algorithm can achieve suboptimality $O(\sqrt{H}/N)$ with high probability if the expert is not constrained to be optimal. Our work formally establishes the benefit of the expert optimal assumption in the known transition setting, while Rajaraman et al (2020) showed it does not help when transitions are unknown.

Missing Mass of Rank-2 Markov Chains

Estimation of missing mass with the popular Good-Turing (GT) estimator is well-understood in the case where samples are independent and identically distributed (iid). In this article, we consider the same problem when the samples come from a stationary Markov chain with a rank-2 transition matrix, which is one of the simplest extensions of the iid case. We develop an upper bound on the absolute bias of the GT estimator in terms of the spectral gap of the chain and a tail bound on the occupancy of states. Borrowing tail bounds from known concentration results for Markov chains, we evaluate the bound using other parameters of the chain. The analysis, supported by simulations, suggests that, for rank-2 irreducible chains, the GT estimator has bias and mean-squared error falling with number of samples at a rate that depends loosely on the connectivity of the states in the chain.