Sample Complexity Bounds for Linear Constrained MDPs with a Generative Model

We consider infinite-horizon $\gamma$-discounted (linear) constrained Markov decision processes (CMDPs) where the objective is to find a policy that maximizes the expected cumulative reward subject to expected cumulative constraints. Given access to a generative model, we propose to solve CMDPs with a primal-dual framework that can leverage any black-box unconstrained MDP solver. For linear CMDPs with feature dimension $d$, we instantiate the framework by using mirror descent value iteration (\texttt{MDVI})~\citep{kitamura2023regularization} an example MDP solver. We provide sample complexity bounds for the resulting CMDP algorithm in two cases: (i) relaxed feasibility, where small constraint violations are allowed, and (ii) strict feasibility, where the output policy is required to exactly satisfy the constraint. For (i), we prove that the algorithm can return an $\epsilon$-optimal policy with high probability by using $\tilde{O}\left(\frac{d^2}{(1-\gamma)^4\epsilon^2}\right)$ samples. We note that these results exhibit a near-optimal dependence on both $d$ and $\epsilon$. For (ii), we show that the algorithm requires $\tilde{O}\left(\frac{d^2}{(1-\gamma)^6\epsilon^2\zeta^2}\right)$ samples, where $\zeta$ is the problem-dependent Slater constant that characterizes the size of the feasible region. Finally, we instantiate our framework for tabular CMDPs and show that it can be used to recover near-optimal sample complexities in this setting.

Does Feedback Help in Bandits with Arm Erasures?

We study a distributed multi-armed bandit (MAB) problem over arm erasure channels, motivated by the increasing adoption of MAB algorithms over communication-constrained networks. In this setup, the learner communicates the chosen arm to play to an agent over an erasure channel with probability $\epsilon \in [0,1)$; if an erasure occurs, the agent continues pulling the last successfully received arm; the learner always observes the reward of the arm pulled. In past work, we considered the case where the agent cannot convey feedback to the learner, and thus the learner does not know whether the arm played is the requested or the last successfully received one. In this paper, we instead consider the case where the agent can send feedback to the learner on whether the arm request was received, and thus the learner exactly knows which arm was played. Surprisingly, we prove that erasure feedback does not improve the worst-case regret upper bound order over the previously studied no-feedback setting. In particular, we prove a regret lower bound of $\Omega(\sqrt{KT} + K / (1 - \epsilon))$, where $K$ is the number of arms and $T$ the time horizon, that matches no-feedback upper bounds up to logarithmic factors. We note however that the availability of feedback enables simpler algorithm designs that may achieve better constants (albeit not better order) regret bounds; we design one such algorithm and evaluate its performance numerically.

NoWag: A Unified Framework for Shape Preserving Compression of Large Language Models

Large language models (LLMs) exhibit remarkable performance across various natural language processing tasks but suffer from immense computational and memory demands, limiting their deployment in resource-constrained environments. To address this challenge, we propose NoWag: (Normalized Weight and Activation Guided Compression), a unified framework for zero-shot shape preserving compression algorithms. We compressed Llama-2 7B/13B/70B and Llama-3 8/70BB models, using two popular forms of shape-preserving compression, vector quantization NoWag-VQ (NoWag for Vector Quantization), and unstructured/semi-structured pruning NoWag-P (NoWag for Pruning). We found that NoWag-VQ significantly outperforms state-of-the-art zero shot VQ, and that NoWag-P performs competitively against state-of-the-art methods. These results suggest commonalities between these compression paradigms that could inspire future work. Our code is available at https://github.com/LawrenceRLiu/NoWag

Hyper: Hyperparameter Robust Efficient Exploration in Reinforcement Learning

The exploration \& exploitation dilemma poses significant challenges in reinforcement learning (RL). Recently, curiosity-based exploration methods achieved great success in tackling hard-exploration problems. However, they necessitate extensive hyperparameter tuning on different environments, which heavily limits the applicability and accessibility of this line of methods. In this paper, we characterize this problem via analysis of the agent behavior, concluding the fundamental difficulty of choosing a proper hyperparameter. We then identify the difficulty and the instability of the optimization when the agent learns with curiosity. We propose our method, hyperparameter robust exploration (\textbf{Hyper}), which extensively mitigates the problem by effectively regularizing the visitation of the exploration and decoupling the exploitation to ensure stable training. We theoretically justify that \textbf{Hyper} is provably efficient under function approximation setting and empirically demonstrate its appealing performance and robustness in various environments.

Misspecified $Q$-Learning with Sparse Linear Function Approximation: Tight Bounds on Approximation Error

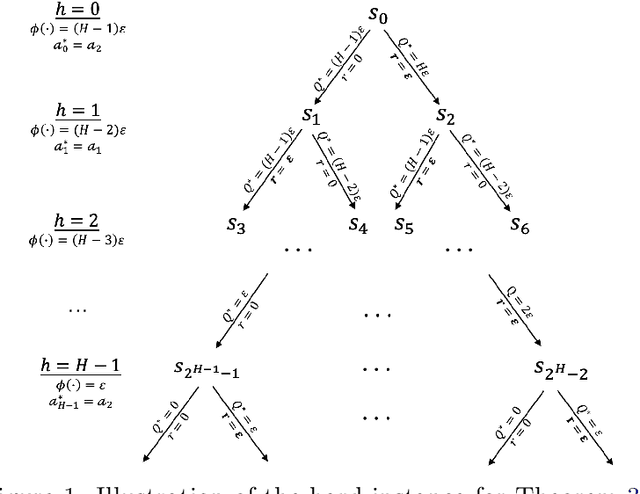
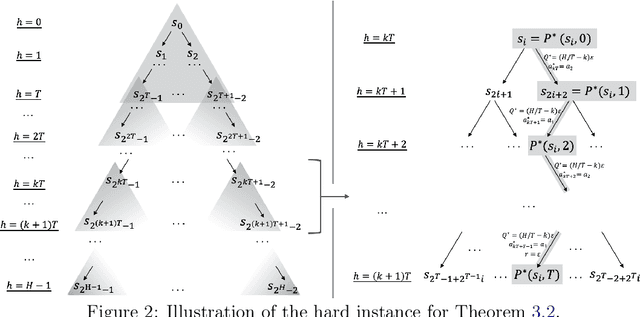
The recent work by Dong & Yang (2023) showed for misspecified sparse linear bandits, one can obtain an $O\left(\epsilon\right)$-optimal policy using a polynomial number of samples when the sparsity is a constant, where $\epsilon$ is the misspecification error. This result is in sharp contrast to misspecified linear bandits without sparsity, which require an exponential number of samples to get the same guarantee. In order to study whether the analog result is possible in the reinforcement learning setting, we consider the following problem: assuming the optimal $Q$-function is a $d$-dimensional linear function with sparsity $k$ and misspecification error $\epsilon$, whether we can obtain an $O\left(\epsilon\right)$-optimal policy using number of samples polynomially in the feature dimension $d$. We first demonstrate why the standard approach based on Bellman backup or the existing optimistic value function elimination approach such as OLIVE (Jiang et al., 2017) achieves suboptimal guarantees for this problem. We then design a novel elimination-based algorithm to show one can obtain an $O\left(H\epsilon\right)$-optimal policy with sample complexity polynomially in the feature dimension $d$ and planning horizon $H$. Lastly, we complement our upper bound with an $\widetilde{\Omega}\left(H\epsilon\right)$ suboptimality lower bound, giving a complete picture of this problem.

Learning for Bandits under Action Erasures

We consider a novel multi-arm bandit (MAB) setup, where a learner needs to communicate the actions to distributed agents over erasure channels, while the rewards for the actions are directly available to the learner through external sensors. In our model, while the distributed agents know if an action is erased, the central learner does not (there is no feedback), and thus does not know whether the observed reward resulted from the desired action or not. We propose a scheme that can work on top of any (existing or future) MAB algorithm and make it robust to action erasures. Our scheme results in a worst-case regret over action-erasure channels that is at most a factor of $O(1/\sqrt{1-\epsilon})$ away from the no-erasure worst-case regret of the underlying MAB algorithm, where $\epsilon$ is the erasure probability. We also propose a modification of the successive arm elimination algorithm and prove that its worst-case regret is $\Tilde{O}(\sqrt{KT}+K/(1-\epsilon))$, which we prove is optimal by providing a matching lower bound.

Confident Natural Policy Gradient for Local Planning in $q_π$-realizable Constrained MDPs

The constrained Markov decision process (CMDP) framework emerges as an important reinforcement learning approach for imposing safety or other critical objectives while maximizing cumulative reward. However, the current understanding of how to learn efficiently in a CMDP environment with a potentially infinite number of states remains under investigation, particularly when function approximation is applied to the value functions. In this paper, we address the learning problem given linear function approximation with $q_{\pi}$-realizability, where the value functions of all policies are linearly representable with a known feature map, a setting known to be more general and challenging than other linear settings. Utilizing a local-access model, we propose a novel primal-dual algorithm that, after $\tilde{O}(\text{poly}(d) \epsilon^{-3})$ queries, outputs with high probability a policy that strictly satisfies the constraints while nearly optimizing the value with respect to a reward function. Here, $d$ is the feature dimension and $\epsilon > 0$ is a given error. The algorithm relies on a carefully crafted off-policy evaluation procedure to evaluate the policy using historical data, which informs policy updates through policy gradients and conserves samples. To our knowledge, this is the first result achieving polynomial sample complexity for CMDP in the $q_{\pi}$-realizable setting.

Don't Forget to Connect! Improving RAG with Graph-based Reranking

Retrieval Augmented Generation (RAG) has greatly improved the performance of Large Language Model (LLM) responses by grounding generation with context from existing documents. These systems work well when documents are clearly relevant to a question context. But what about when a document has partial information, or less obvious connections to the context? And how should we reason about connections between documents? In this work, we seek to answer these two core questions about RAG generation. We introduce G-RAG, a reranker based on graph neural networks (GNNs) between the retriever and reader in RAG. Our method combines both connections between documents and semantic information (via Abstract Meaning Representation graphs) to provide a context-informed ranker for RAG. G-RAG outperforms state-of-the-art approaches while having smaller computational footprint. Additionally, we assess the performance of PaLM 2 as a reranker and find it to significantly underperform G-RAG. This result emphasizes the importance of reranking for RAG even when using Large Language Models.

Multi-Agent Bandit Learning through Heterogeneous Action Erasure Channels

Multi-Armed Bandit (MAB) systems are witnessing an upswing in applications within multi-agent distributed environments, leading to the advancement of collaborative MAB algorithms. In such settings, communication between agents executing actions and the primary learner making decisions can hinder the learning process. A prevalent challenge in distributed learning is action erasure, often induced by communication delays and/or channel noise. This results in agents possibly not receiving the intended action from the learner, subsequently leading to misguided feedback. In this paper, we introduce novel algorithms that enable learners to interact concurrently with distributed agents across heterogeneous action erasure channels with different action erasure probabilities. We illustrate that, in contrast to existing bandit algorithms, which experience linear regret, our algorithms assure sub-linear regret guarantees. Our proposed solutions are founded on a meticulously crafted repetition protocol and scheduling of learning across heterogeneous channels. To our knowledge, these are the first algorithms capable of effectively learning through heterogeneous action erasure channels. We substantiate the superior performance of our algorithm through numerical experiments, emphasizing their practical significance in addressing issues related to communication constraints and delays in multi-agent environments.

Horizon-Free and Instance-Dependent Regret Bounds for Reinforcement Learning with General Function Approximation

To tackle long planning horizon problems in reinforcement learning with general function approximation, we propose the first algorithm, termed as UCRL-WVTR, that achieves both \emph{horizon-free} and \emph{instance-dependent}, since it eliminates the polynomial dependency on the planning horizon. The derived regret bound is deemed \emph{sharp}, as it matches the minimax lower bound when specialized to linear mixture MDPs up to logarithmic factors. Furthermore, UCRL-WVTR is \emph{computationally efficient} with access to a regression oracle. The achievement of such a horizon-free, instance-dependent, and sharp regret bound hinges upon (i) novel algorithm designs: weighted value-targeted regression and a high-order moment estimator in the context of general function approximation; and (ii) fine-grained analyses: a novel concentration bound of weighted non-linear least squares and a refined analysis which leads to the tight instance-dependent bound. We also conduct comprehensive experiments to corroborate our theoretical findings.