Active-SWE: Benchmarking Coding Agents for Proactive Bug Fixing without Issue Reports

Coding agents powered by large language models (LLMs) are increasingly adopted in software engineering (SWE) scenarios, capable of fixing a specific bug in large-scale codebase. However, existing SWE benchmarks typically assume that high-quality issue reports with detailed information are always available, which is easily violated in practice due to the complexity of report acquisition and curation. To address this, we introduce Active-SWE, a benchmark for evaluating coding agents on proactively discovering and fixing multiple bugs without report guidance, covering 1,663 tasks across six bug categories and eight languages. Beyond shifting the focus from existing reactive bug fixing to proactive bug fixing, Active-SWE enables a more in-depth evaluation by expanding the scope from fixing a specific recorded bug to multiple-bug fixing and potential bug discovery scenarios. To construct Active-SWE, we propose a novel difficulty-aware task formulation pipeline with a dual-track evaluation framework, facilitating comprehensive evaluation of proactive bug-fixing capability. Extensive experiments reveal that most state-of-the-art coding agents struggle with proactive bug-fixing tasks, demonstrating limited performance in locating and resolving recorded bugs, handling multiple bug fixing scenarios, and discovering valid potential bugs.

Ling and Ring 2.6 Technical Report: Efficient and Instant Agentic Intelligence at Trillion-Parameter Scale

Efficient and scalable agentic intelligence requires models that can deliver both low-latency responses and strong reasoning capabilities while remaining practical to train, serve, and deploy. In this report, we present Ling-2.6 and Ring-2.6, a family of models designed to address this challenge at scale. Ling-2.6 is optimized for instant response generation and high capability per output token, whereas Ring-2.6 is tailored for deeper reasoning and more advanced agentic workflows. Instead of training from scratch, we upgrade the Ling-2.0 base model through architectural migration pre-training and large-scale post-training. This upgrade is guided by a unified co-design of model architecture, optimization objectives, serving systems, and agent training environments, enabling improvements in both model capability and deployment efficiency. At the architectural level, we introduce a hybrid linear attention design that integrates Lightning Attention with MLA, improving the efficiency of long-context training and decoding. To further enhance token efficiency, we optimize capability per output token through Evolutionary Chain-of-Thought, Linguistic Unit Policy Optimization, bidirectional preference alignment, and shortest-correct-response distillation. For agentic capabilities, we propose KPop, a reinforcement learning framework designed to support stable training of Ring-2.6-1T on large-scale environment-grounded data. KPop improves training efficiency through asynchronous scheduling across coding, search, tool use, and workflow execution, enabling scalable learning from complex agent-environment interactions. Together, Ling-2.6 and Ring-2.6 provide a practical pathway toward efficient, scalable, and open agentic systems. We open-source all checkpoints in the 2.6 family to support further research and development in practical agentic intelligence.

InftyThink+: Effective and Efficient Infinite-Horizon Reasoning via Reinforcement Learning

Large reasoning models achieve strong performance by scaling inference-time chain-of-thought, but this paradigm suffers from quadratic cost, context length limits, and degraded reasoning due to lost-in-the-middle effects. Iterative reasoning mitigates these issues by periodically summarizing intermediate thoughts, yet existing methods rely on supervised learning or fixed heuristics and fail to optimize when to summarize, what to preserve, and how to resume reasoning. We propose InftyThink+, an end-to-end reinforcement learning framework that optimizes the entire iterative reasoning trajectory, building on model-controlled iteration boundaries and explicit summarization. InftyThink+ adopts a two-stage training scheme with supervised cold-start followed by trajectory-level reinforcement learning, enabling the model to learn strategic summarization and continuation decisions. Experiments on DeepSeek-R1-Distill-Qwen-1.5B show that InftyThink+ improves accuracy by 21% on AIME24 and outperforms conventional long chain-of-thought reinforcement learning by a clear margin, while also generalizing better to out-of-distribution benchmarks. Moreover, InftyThink+ significantly reduces inference latency and accelerates reinforcement learning training, demonstrating improved reasoning efficiency alongside stronger performance.

Every Step Evolves: Scaling Reinforcement Learning for Trillion-Scale Thinking Model

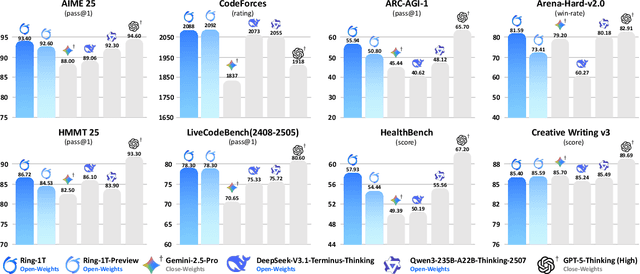
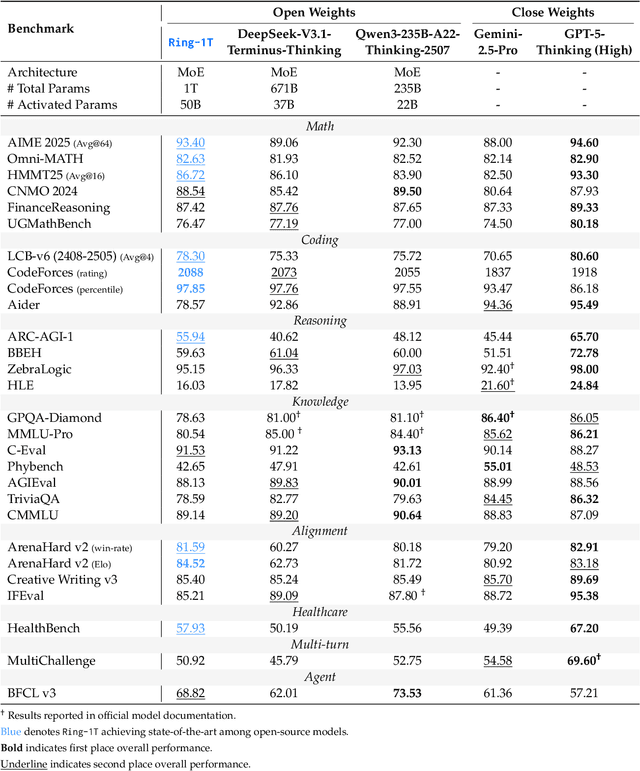
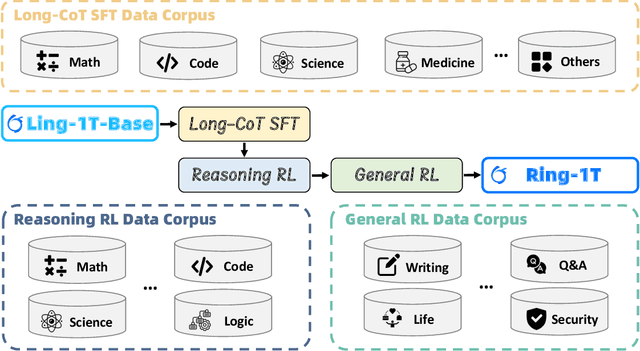
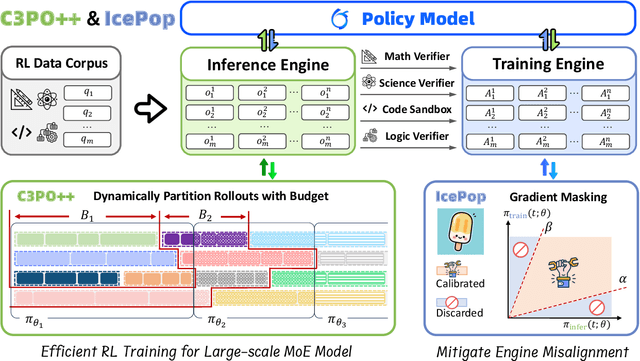
We present Ring-1T, the first open-source, state-of-the-art thinking model with a trillion-scale parameter. It features 1 trillion total parameters and activates approximately 50 billion per token. Training such models at a trillion-parameter scale introduces unprecedented challenges, including train-inference misalignment, inefficiencies in rollout processing, and bottlenecks in the RL system. To address these, we pioneer three interconnected innovations: (1) IcePop stabilizes RL training via token-level discrepancy masking and clipping, resolving instability from training-inference mismatches; (2) C3PO++ improves resource utilization for long rollouts under a token budget by dynamically partitioning them, thereby obtaining high time efficiency; and (3) ASystem, a high-performance RL framework designed to overcome the systemic bottlenecks that impede trillion-parameter model training. Ring-1T delivers breakthrough results across critical benchmarks: 93.4 on AIME-2025, 86.72 on HMMT-2025, 2088 on CodeForces, and 55.94 on ARC-AGI-v1. Notably, it attains a silver medal-level result on the IMO-2025, underscoring its exceptional reasoning capabilities. By releasing the complete 1T parameter MoE model to the community, we provide the research community with direct access to cutting-edge reasoning capabilities. This contribution marks a significant milestone in democratizing large-scale reasoning intelligence and establishes a new baseline for open-source model performance.

Ring-lite: Scalable Reasoning via C3PO-Stabilized Reinforcement Learning for LLMs

We present Ring-lite, a Mixture-of-Experts (MoE)-based large language model optimized via reinforcement learning (RL) to achieve efficient and robust reasoning capabilities. Built upon the publicly available Ling-lite model, a 16.8 billion parameter model with 2.75 billion activated parameters, our approach matches the performance of state-of-the-art (SOTA) small-scale reasoning models on challenging benchmarks (e.g., AIME, LiveCodeBench, GPQA-Diamond) while activating only one-third of the parameters required by comparable models. To accomplish this, we introduce a joint training pipeline integrating distillation with RL, revealing undocumented challenges in MoE RL training. First, we identify optimization instability during RL training, and we propose Constrained Contextual Computation Policy Optimization(C3PO), a novel approach that enhances training stability and improves computational throughput via algorithm-system co-design methodology. Second, we empirically demonstrate that selecting distillation checkpoints based on entropy loss for RL training, rather than validation metrics, yields superior performance-efficiency trade-offs in subsequent RL training. Finally, we develop a two-stage training paradigm to harmonize multi-domain data integration, addressing domain conflicts that arise in training with mixed dataset. We will release the model, dataset, and code.

Holistic Capability Preservation: Towards Compact Yet Comprehensive Reasoning Models

This technical report presents Ring-Lite-Distill, a lightweight reasoning model derived from our open-source Mixture-of-Experts (MoE) Large Language Models (LLMs) Ling-Lite. This study demonstrates that through meticulous high-quality data curation and ingenious training paradigms, the compact MoE model Ling-Lite can be further trained to achieve exceptional reasoning capabilities, while maintaining its parameter-efficient architecture with only 2.75 billion activated parameters, establishing an efficient lightweight reasoning architecture. In particular, in constructing this model, we have not merely focused on enhancing advanced reasoning capabilities, exemplified by high-difficulty mathematical problem solving, but rather aimed to develop a reasoning model with more comprehensive competency coverage. Our approach ensures coverage across reasoning tasks of varying difficulty levels while preserving generic capabilities, such as instruction following, tool use, and knowledge retention. We show that, Ring-Lite-Distill's reasoning ability reaches a level comparable to DeepSeek-R1-Distill-Qwen-7B, while its general capabilities significantly surpass those of DeepSeek-R1-Distill-Qwen-7B. The models are accessible at https://huggingface.co/inclusionAI

Towards efficient and secure quantum-classical communication networks

The rapid advancement of quantum technologies calls for the design and deployment of quantum-safe cryptographic protocols and communication networks. There are two primary approaches to achieving quantum-resistant security: quantum key distribution (QKD) and post-quantum cryptography (PQC). While each offers unique advantages, both have drawbacks in practical implementation. In this work, we introduce the pros and cons of these protocols and explore how they can be combined to achieve a higher level of security and/or improved performance in key distribution. We hope our discussion inspires further research into the design of hybrid cryptographic protocols for quantum-classical communication networks.

Practical hybrid PQC-QKD protocols with enhanced security and performance

Quantum resistance is vital for emerging cryptographic systems as quantum technologies continue to advance towards large-scale, fault-tolerant quantum computers. Resistance may be offered by quantum key distribution (QKD), which provides information-theoretic security using quantum states of photons, but may be limited by transmission loss at long distances. An alternative approach uses classical means and is conjectured to be resistant to quantum attacks, so-called post-quantum cryptography (PQC), but it is yet to be rigorously proven, and its current implementations are computationally expensive. To overcome the security and performance challenges present in each, here we develop hybrid protocols by which QKD and PQC inter-operate within a joint quantum-classical network. In particular, we consider different hybrid designs that may offer enhanced speed and/or security over the individual performance of either approach. Furthermore, we present a method for analyzing the security of hybrid protocols in key distribution networks. Our hybrid approach paves the way for joint quantum-classical communication networks, which leverage the advantages of both QKD and PQC and can be tailored to the requirements of various practical networks.

Quantum-data-driven dynamical transition in quantum learning

Quantum circuits are an essential ingredient of quantum information processing. Parameterized quantum circuits optimized under a specific cost function -- quantum neural networks (QNNs) -- provide a paradigm for achieving quantum advantage in the near term. Understanding QNN training dynamics is crucial for optimizing their performance. In terms of supervised learning tasks such as classification and regression for large datasets, the role of quantum data in QNN training dynamics remains unclear. We reveal a quantum-data-driven dynamical transition, where the target value and data determine the polynomial or exponential convergence of the training. We analytically derive the complete classification of fixed points from the dynamical equation and reveal a comprehensive `phase diagram' featuring seven distinct dynamics. These dynamics originate from a bifurcation transition with multiple codimensions induced by training data, extending the transcritical bifurcation in simple optimization tasks. Furthermore, perturbative analyses identify an exponential convergence class and a polynomial convergence class among the seven dynamics. We provide a non-perturbative theory to explain the transition via generalized restricted Haar ensemble. The analytical results are confirmed with numerical simulations of QNN training and experimental verification on IBM quantum devices. As the QNN training dynamics is determined by the choice of the target value, our findings provide guidance on constructing the cost function to optimize the speed of convergence.

The curse of random quantum data

Quantum machine learning, which involves running machine learning algorithms on quantum devices, may be one of the most significant flagship applications for these devices. Unlike its classical counterparts, the role of data in quantum machine learning has not been fully understood. In this work, we quantify the performances of quantum machine learning in the landscape of quantum data. Provided that the encoding of quantum data is sufficiently random, the performance, we find that the training efficiency and generalization capabilities in quantum machine learning will be exponentially suppressed with the increase in the number of qubits, which we call "the curse of random quantum data". Our findings apply to both the quantum kernel method and the large-width limit of quantum neural networks. Conversely, we highlight that through meticulous design of quantum datasets, it is possible to avoid these curses, thereby achieving efficient convergence and robust generalization. Our conclusions are corroborated by extensive numerical simulations.