Min-Hsiu Hsieh
Random-Matrix-Induced Simplicity Bias in Over-parameterized Variational Quantum Circuits
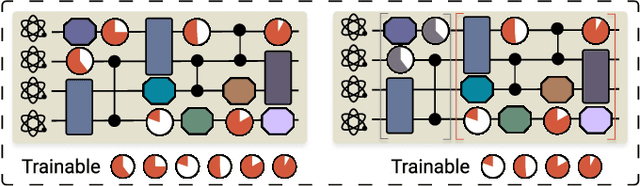
Jan 05, 2026Abstract:Over-parameterization is commonly used to increase the expressivity of variational quantum circuits (VQCs), yet deeper and more highly parameterized circuits often exhibit poor trainability and limited generalization. In this work, we provide a theoretical explanation for this phenomenon from a function-class perspective. We show that sufficiently expressive, unstructured variational ansatze enter a Haar-like universality class in which both observable expectation values and parameter gradients concentrate exponentially with system size. As a consequence, the hypothesis class induced by such circuits collapses with high probability to a narrow family of near-constant functions, a phenomenon we term simplicity bias, with barren plateaus arising as a consequence rather than the root cause. Using tools from random matrix theory and concentration of measure, we rigorously characterize this universality class and establish uniform hypothesis-class collapse over finite datasets. We further show that this collapse is not unavoidable: tensor-structured VQCs, including tensor-network-based and tensor-hypernetwork parameterizations, lie outside the Haar-like universality class. By restricting the accessible unitary ensemble through bounded tensor rank or bond dimension, these architectures prevent concentration of measure, preserve output variability for local observables, and retain non-degenerate gradient signals even in over-parameterized regimes. Together, our results unify barren plateaus, expressivity limits, and generalization collapse under a single structural mechanism rooted in random-matrix universality, highlighting the central role of architectural inductive bias in variational quantum algorithms.
Artificial intelligence for representing and characterizing quantum systems
Sep 05, 2025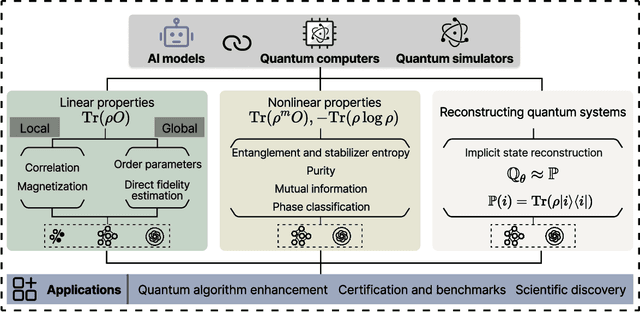

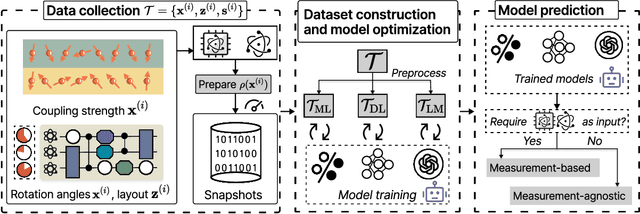
Abstract:Efficient characterization of large-scale quantum systems, especially those produced by quantum analog simulators and megaquop quantum computers, poses a central challenge in quantum science due to the exponential scaling of the Hilbert space with respect to system size. Recent advances in artificial intelligence (AI), with its aptitude for high-dimensional pattern recognition and function approximation, have emerged as a powerful tool to address this challenge. A growing body of research has leveraged AI to represent and characterize scalable quantum systems, spanning from theoretical foundations to experimental realizations. Depending on how prior knowledge and learning architectures are incorporated, the integration of AI into quantum system characterization can be categorized into three synergistic paradigms: machine learning, and, in particular, deep learning and language models. This review discusses how each of these AI paradigms contributes to two core tasks in quantum systems characterization: quantum property prediction and the construction of surrogates for quantum states. These tasks underlie diverse applications, from quantum certification and benchmarking to the enhancement of quantum algorithms and the understanding of strongly correlated phases of matter. Key challenges and open questions are also discussed, together with future prospects at the interface of AI and quantum science.
VQC-MLPNet: An Unconventional Hybrid Quantum-Classical Architecture for Scalable and Robust Quantum Machine Learning
Jun 12, 2025Abstract:Variational Quantum Circuits (VQCs) offer a novel pathway for quantum machine learning, yet their practical application is hindered by inherent limitations such as constrained linear expressivity, optimization challenges, and acute sensitivity to quantum hardware noise. This work introduces VQC-MLPNet, a scalable and robust hybrid quantum-classical architecture designed to overcome these obstacles. By innovatively employing quantum circuits to dynamically generate parameters for classical Multi-Layer Perceptrons (MLPs) via amplitude encoding and parameterized quantum operations, VQC-MLPNet substantially expands representation capabilities and augments training stability. We provide rigorous theoretical guarantees via statistical learning techniques and Neural Tangent Kernel analysis, explicitly deriving upper bounds on approximation, uniform deviation, and optimization errors. These theoretical insights demonstrate exponential improvements in representation capacity relative to quantum circuit depth and the number of qubits, providing clear computational advantages over standalone quantum circuits and existing hybrid quantum architectures. Our theoretical claims are empirically corroborated through extensive experiments, including classifying semiconductor quantum-dot charge states and predicting genomic transcription factor binding sites, demonstrating resilient performance even under realistic IBM quantum noise simulations. This research establishes a theoretically sound and practically robust framework, advancing the frontiers of quantum-enhanced learning for unconventional computing paradigms in the Noisy Intermediate-Scale Quantum era and beyond.
Quantum Machine Learning: A Hands-on Tutorial for Machine Learning Practitioners and Researchers
Feb 03, 2025Abstract:This tutorial intends to introduce readers with a background in AI to quantum machine learning (QML) -- a rapidly evolving field that seeks to leverage the power of quantum computers to reshape the landscape of machine learning. For self-consistency, this tutorial covers foundational principles, representative QML algorithms, their potential applications, and critical aspects such as trainability, generalization, and computational complexity. In addition, practical code demonstrations are provided in https://qml-tutorial.github.io/ to illustrate real-world implementations and facilitate hands-on learning. Together, these elements offer readers a comprehensive overview of the latest advancements in QML. By bridging the gap between classical machine learning and quantum computing, this tutorial serves as a valuable resource for those looking to engage with QML and explore the forefront of AI in the quantum era.
Efficient Learning for Linear Properties of Bounded-Gate Quantum Circuits
Aug 22, 2024Abstract:The vast and complicated large-qubit state space forbids us to comprehensively capture the dynamics of modern quantum computers via classical simulations or quantum tomography. However, recent progress in quantum learning theory invokes a crucial question: given a quantum circuit containing d tunable RZ gates and G-d Clifford gates, can a learner perform purely classical inference to efficiently predict its linear properties using new classical inputs, after learning from data obtained by incoherently measuring states generated by the same circuit but with different classical inputs? In this work, we prove that the sample complexity scaling linearly in d is necessary and sufficient to achieve a small prediction error, while the corresponding computational complexity may scale exponentially in d. Building upon these derived complexity bounds, we further harness the concept of classical shadow and truncated trigonometric expansion to devise a kernel-based learning model capable of trading off prediction error and computational complexity, transitioning from exponential to polynomial scaling in many practical settings. Our results advance two crucial realms in quantum computation: the exploration of quantum algorithms with practical utilities and learning-based quantum system certification. We conduct numerical simulations to validate our proposals across diverse scenarios, encompassing quantum information processing protocols, Hamiltonian simulation, and variational quantum algorithms up to 60 qubits.
The curse of random quantum data
Aug 19, 2024Abstract:Quantum machine learning, which involves running machine learning algorithms on quantum devices, may be one of the most significant flagship applications for these devices. Unlike its classical counterparts, the role of data in quantum machine learning has not been fully understood. In this work, we quantify the performances of quantum machine learning in the landscape of quantum data. Provided that the encoding of quantum data is sufficiently random, the performance, we find that the training efficiency and generalization capabilities in quantum machine learning will be exponentially suppressed with the increase in the number of qubits, which we call "the curse of random quantum data". Our findings apply to both the quantum kernel method and the large-width limit of quantum neural networks. Conversely, we highlight that through meticulous design of quantum datasets, it is possible to avoid these curses, thereby achieving efficient convergence and robust generalization. Our conclusions are corroborated by extensive numerical simulations.
Demystify Problem-Dependent Power of Quantum Neural Networks on Multi-Class Classification
Dec 29, 2022



Abstract:Quantum neural networks (QNNs) have become an important tool for understanding the physical world, but their advantages and limitations are not fully understood. Some QNNs with specific encoding methods can be efficiently simulated by classical surrogates, while others with quantum memory may perform better than classical classifiers. Here we systematically investigate the problem-dependent power of quantum neural classifiers (QCs) on multi-class classification tasks. Through the analysis of expected risk, a measure that weighs the training loss and the generalization error of a classifier jointly, we identify two key findings: first, the training loss dominates the power rather than the generalization ability; second, QCs undergo a U-shaped risk curve, in contrast to the double-descent risk curve of deep neural classifiers. We also reveal the intrinsic connection between optimal QCs and the Helstrom bound and the equiangular tight frame. Using these findings, we propose a method that uses loss dynamics to probe whether a QC may be more effective than a classical classifier on a particular learning task. Numerical results demonstrate the effectiveness of our approach to explain the superiority of QCs over multilayer Perceptron on parity datasets and their limitations over convolutional neural networks on image datasets. Our work sheds light on the problem-dependent power of QNNs and offers a practical tool for evaluating their potential merit.
Implementation of Trained Factorization Machine Recommendation System on Quantum Annealer
Oct 24, 2022



Abstract:Factorization Machine (FM) is the most commonly used model to build a recommendation system since it can incorporate side information to improve performance. However, producing item suggestions for a given user with a trained FM is time-consuming. It requires a run-time of $O((N_m \log N_m)^2)$, where $N_m$ is the number of items in the dataset. To address this problem, we propose a quadratic unconstrained binary optimization (QUBO) scheme to combine with FM and apply quantum annealing (QA) computation. Compared to classical methods, this hybrid algorithm provides a faster than quadratic speedup in finding good user suggestions. We then demonstrate the aforementioned computational advantage on current NISQ hardware by experimenting with a real example on a D-Wave annealer.
Theoretical Error Performance Analysis for Variational Quantum Circuit Based Functional Regression
Jun 08, 2022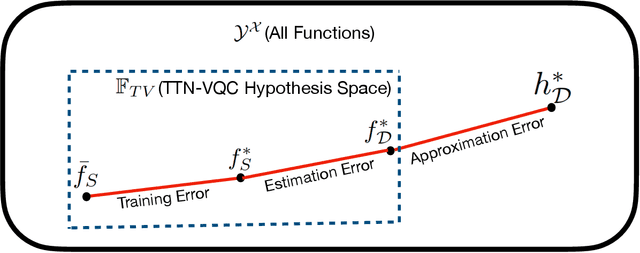

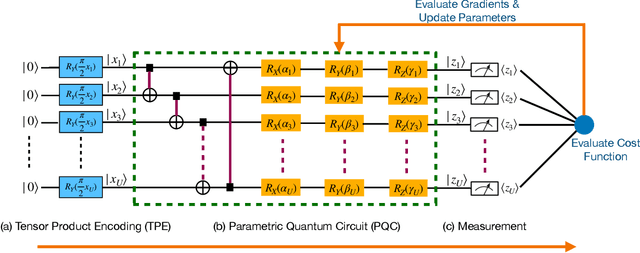
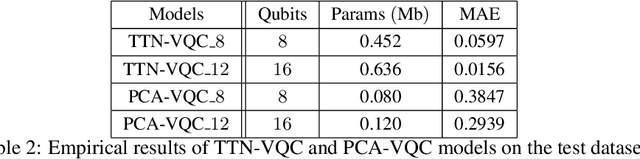
Abstract:The noisy intermediate-scale quantum (NISQ) devices enable the implementation of the variational quantum circuit (VQC) for quantum neural networks (QNN). Although the VQC-based QNN has succeeded in many machine learning tasks, the representation and generalization powers of VQC still require further investigation, particularly when the dimensionality reduction of classical inputs is concerned. In this work, we first put forth an end-to-end quantum neural network, namely, TTN-VQC, which consists of a quantum tensor network based on a tensor-train network (TTN) for dimensionality reduction and a VQC for functional regression. Then, we aim at the error performance analysis for the TTN-VQC in terms of representation and generalization powers. We also characterize the optimization properties of TTN-VQC by leveraging the Polyak-Lojasiewicz (PL) condition. Moreover, we conduct the experiments of functional regression on a handwritten digit classification dataset to justify our theoretical analysis.
Recent Advances for Quantum Neural Networks in Generative Learning
Jun 07, 2022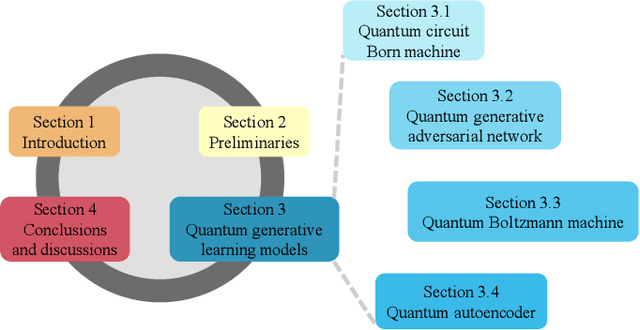

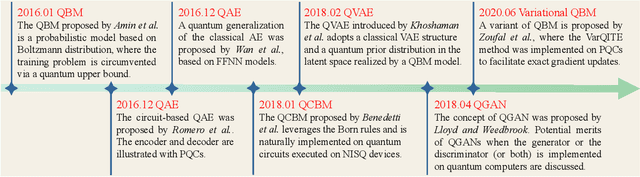
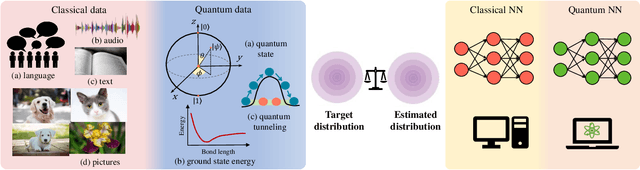
Abstract:Quantum computers are next-generation devices that hold promise to perform calculations beyond the reach of classical computers. A leading method towards achieving this goal is through quantum machine learning, especially quantum generative learning. Due to the intrinsic probabilistic nature of quantum mechanics, it is reasonable to postulate that quantum generative learning models (QGLMs) may surpass their classical counterparts. As such, QGLMs are receiving growing attention from the quantum physics and computer science communities, where various QGLMs that can be efficiently implemented on near-term quantum machines with potential computational advantages are proposed. In this paper, we review the current progress of QGLMs from the perspective of machine learning. Particularly, we interpret these QGLMs, covering quantum circuit born machines, quantum generative adversarial networks, quantum Boltzmann machines, and quantum autoencoders, as the quantum extension of classical generative learning models. In this context, we explore their intrinsic relation and their fundamental differences. We further summarize the potential applications of QGLMs in both conventional machine learning tasks and quantum physics. Last, we discuss the challenges and further research directions for QGLMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge