Mixed-State Quantum Denoising Diffusion Probabilistic Model

Generative quantum machine learning has gained significant attention for its ability to produce quantum states with desired distributions. Among various quantum generative models, quantum denoising diffusion probabilistic models (QuDDPMs) [Phys. Rev. Lett. 132, 100602 (2024)] provide a promising approach with stepwise learning that resolves the training issues. However, the requirement of high-fidelity scrambling unitaries in QuDDPM poses a challenge in near-term implementation. We propose the \textit{mixed-state quantum denoising diffusion probabilistic model} (MSQuDDPM) to eliminate the need for scrambling unitaries. Our approach focuses on adapting the quantum noise channels to the model architecture, which integrates depolarizing noise channels in the forward diffusion process and parameterized quantum circuits with projective measurements in the backward denoising steps. We also introduce several techniques to improve MSQuDDPM, including a cosine-exponent schedule of noise interpolation, the use of single-qubit random ancilla, and superfidelity-based cost functions to enhance the convergence. We evaluate MSQuDDPM on quantum ensemble generation tasks, demonstrating its successful performance.

Quantum-data-driven dynamical transition in quantum learning

Quantum circuits are an essential ingredient of quantum information processing. Parameterized quantum circuits optimized under a specific cost function -- quantum neural networks (QNNs) -- provide a paradigm for achieving quantum advantage in the near term. Understanding QNN training dynamics is crucial for optimizing their performance. In terms of supervised learning tasks such as classification and regression for large datasets, the role of quantum data in QNN training dynamics remains unclear. We reveal a quantum-data-driven dynamical transition, where the target value and data determine the polynomial or exponential convergence of the training. We analytically derive the complete classification of fixed points from the dynamical equation and reveal a comprehensive `phase diagram' featuring seven distinct dynamics. These dynamics originate from a bifurcation transition with multiple codimensions induced by training data, extending the transcritical bifurcation in simple optimization tasks. Furthermore, perturbative analyses identify an exponential convergence class and a polynomial convergence class among the seven dynamics. We provide a non-perturbative theory to explain the transition via generalized restricted Haar ensemble. The analytical results are confirmed with numerical simulations of QNN training and experimental verification on IBM quantum devices. As the QNN training dynamics is determined by the choice of the target value, our findings provide guidance on constructing the cost function to optimize the speed of convergence.

Dynamical phase transition in quantum neural networks with large depth

Understanding the training dynamics of quantum neural networks is a fundamental task in quantum information science with wide impact in physics, chemistry and machine learning. In this work, we show that the late-time training dynamics of quantum neural networks can be described by the generalized Lotka-Volterra equations, which lead to a dynamical phase transition. When the targeted value of cost function crosses the minimum achievable value from above to below, the dynamics evolve from a frozen-kernel phase to a frozen-error phase, showing a duality between the quantum neural tangent kernel and the total error. In both phases, the convergence towards the fixed point is exponential, while at the critical point becomes polynomial. Via mapping the Hessian of the training dynamics to a Hamiltonian in the imaginary time, we reveal the nature of the phase transition to be second-order with the exponent $\nu=1$, where scale invariance and closing gap are observed at critical point. We also provide a non-perturbative analytical theory to explain the phase transition via a restricted Haar ensemble at late time, when the output state approaches the steady state. The theory findings are verified experimentally on IBM quantum devices.

Generative quantum machine learning via denoising diffusion probabilistic models

Deep generative models are key-enabling technology to computer vision, text generation and large language models. Denoising diffusion probabilistic models (DDPMs) have recently gained much attention due to their ability to generate diverse and high-quality samples in many computer vision tasks, as well as to incorporate flexible model architectures and relatively simple training scheme. Quantum generative models, empowered by entanglement and superposition, have brought new insight to learning classical and quantum data. Inspired by the classical counterpart, we propose the quantum denoising diffusion probabilistic models (QuDDPM) to enable efficiently trainable generative learning of quantum data. QuDDPM adopts sufficient layers of circuits to guarantee expressivity, while introduces multiple intermediate training tasks as interpolation between the target distribution and noise to avoid barren plateau and guarantee efficient training. We demonstrate QuDDPM's capability in learning correlated quantum noise model and learning topological structure of nontrivial distribution of quantum data.

Energy-dependent barren plateau in bosonic variational quantum circuits

Bosonic continuous-variable Variational quantum circuits (VQCs) are crucial for information processing in cavity quantum electrodynamics and optical systems, widely applicable in quantum communication, sensing and error correction. The trainability of such VQCs is less understood, hindered by the lack of theoretical tools such as $t$-design due to the infinite dimension of the physical systems involved. We overcome this difficulty to reveal an energy-dependent barren plateau in such VQCs. The variance of the gradient decays as $1/E^{M\nu}$, exponential in the number of modes $M$ but polynomial in the (per-mode) circuit energy $E$. The exponent $\nu=1$ for shallow circuits and $\nu=2$ for deep circuits. We prove these results for state preparation of general Gaussian states and number states. We also provide numerical evidence that the results extend to general state preparation tasks. As circuit energy is a controllable parameter, we provide a strategy to mitigate the barren plateau in continuous-variable VQCs.

Information contraction in noisy binary neural networks and its implications

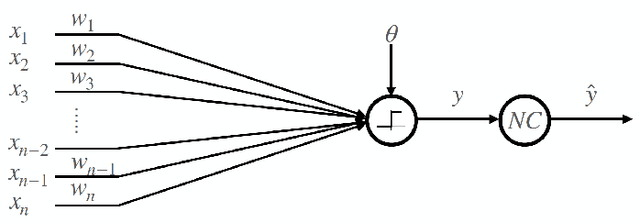
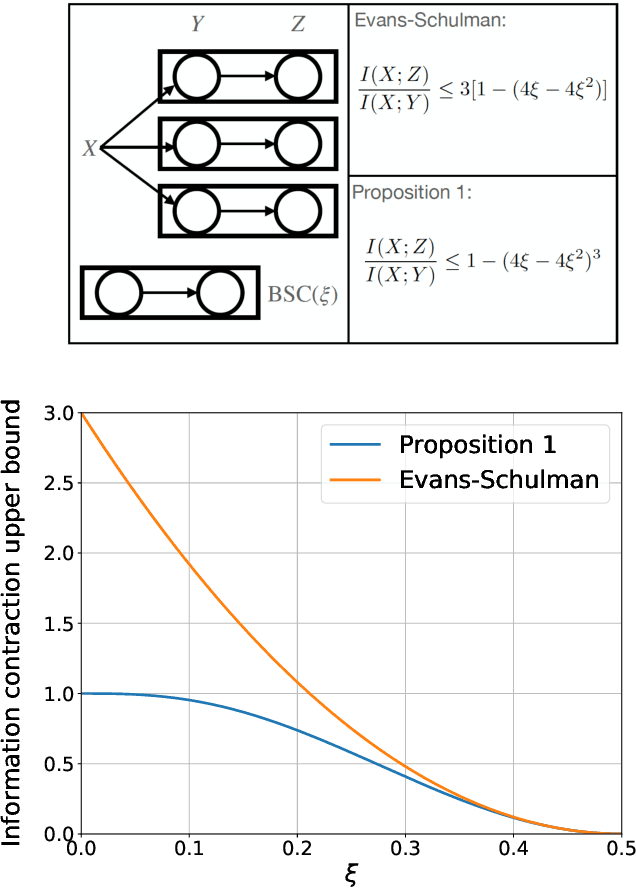
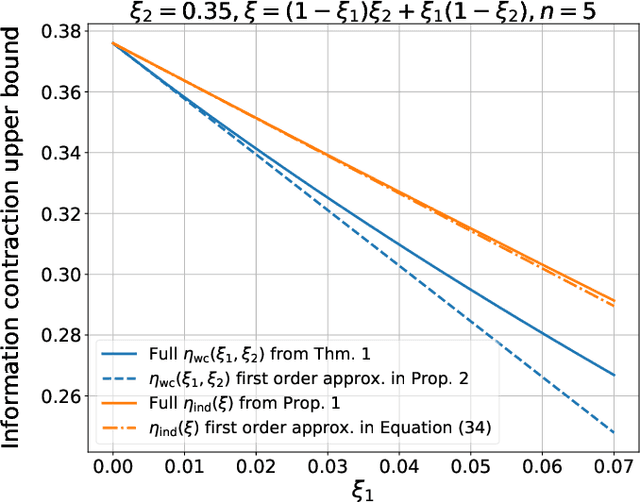
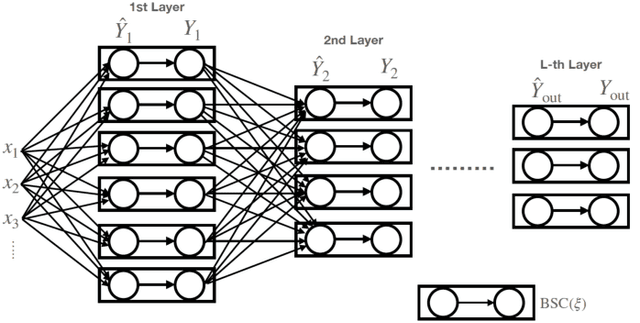
Neural networks have gained importance as the machine learning models that achieve state-of-the-art performance on large-scale image classification, object detection and natural language processing tasks. In this paper, we consider noisy binary neural networks, where each neuron has a non-zero probability of producing an incorrect output. These noisy models may arise from biological, physical and electronic contexts and constitute an important class of models that are relevant to the physical world. Intuitively, the number of neurons in such systems has to grow to compensate for the noise while maintaining the same level of expressive power and computation reliability. Our key finding is a lower bound for the required number of neurons in noisy neural networks, which is first of its kind. To prove this lower bound, we take an information theoretic approach and obtain a novel strong data processing inequality (SDPI), which not only generalizes the Evans-Schulman results for binary symmetric channels to general channels, but also improves the tightness drastically when applied to estimate end-to-end information contraction in networks. Our SDPI can be applied to various information processing systems, including neural networks and cellular automata. Applying the SDPI in noisy binary neural networks, we obtain our key lower bound and investigate its implications on network depth-width trade-offs, our results suggest a depth-width trade-off for noisy neural networks that is very different from the established understanding regarding noiseless neural networks. Furthermore, we apply the SDPI to study fault-tolerant cellular automata and obtain bounds on the error correction overheads and the relaxation time. This paper offers new understanding of noisy information processing systems through the lens of information theory.

Quantum-enhanced barcode decoding and pattern recognition

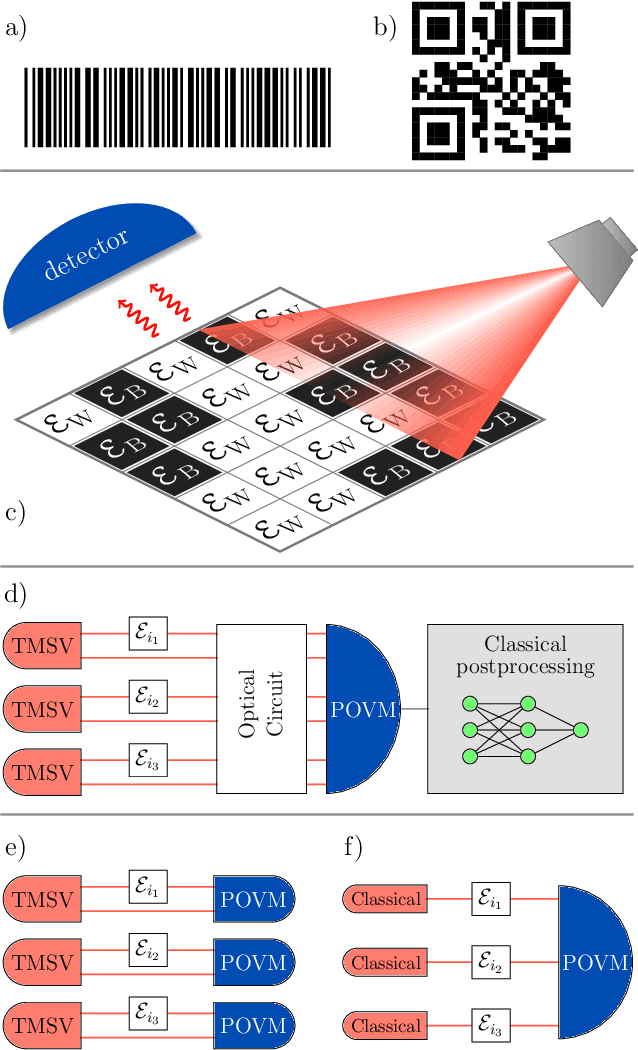
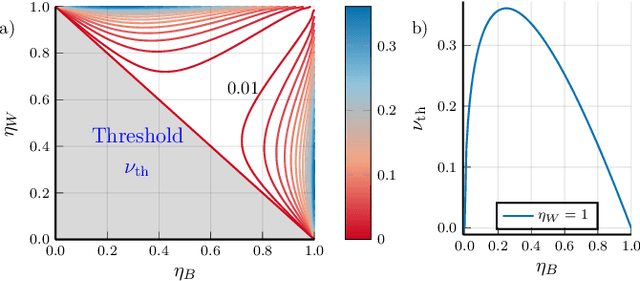
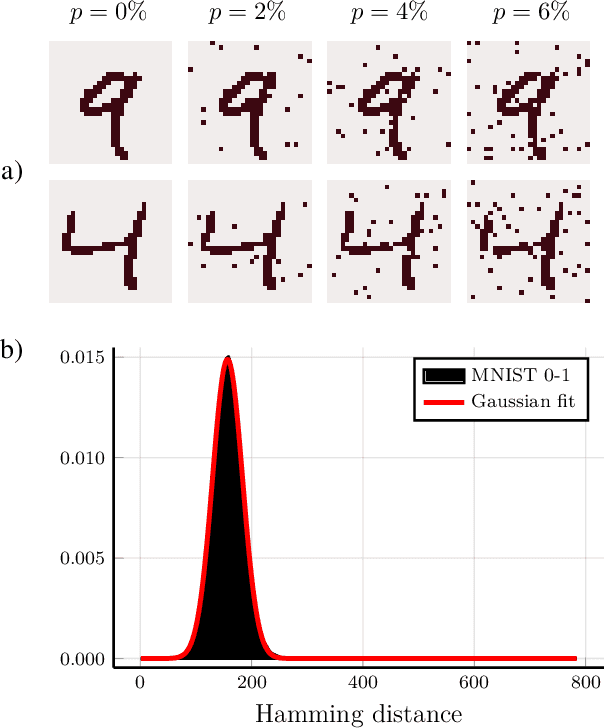
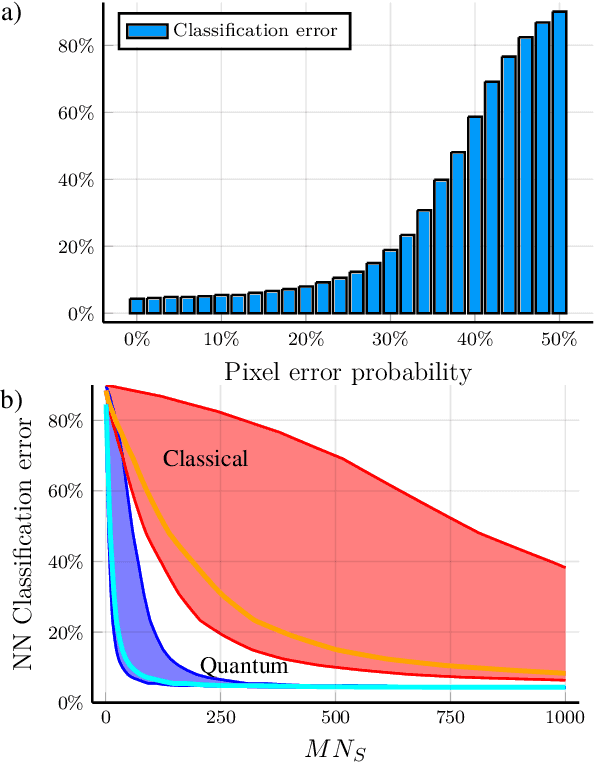
Quantum hypothesis testing is one of the most fundamental problems in quantum information theory, with crucial implications in areas like quantum sensing, where it has been used to prove quantum advantage in a series of binary photonic protocols, e.g., for target detection or memory cell readout. In this work, we generalize this theoretical model to the multi-partite setting of barcode decoding and pattern recognition. We start by defining a digital image as an array or grid of pixels, each pixel corresponding to an ensemble of quantum channels. Specializing each pixel to a black and white alphabet, we naturally define an optical model of barcode. In this scenario, we show that the use of quantum entangled sources, combined with suitable measurements and data processing, greatly outperforms classical coherent-state strategies for the tasks of barcode data decoding and classification of black and white patterns. Moreover, introducing relevant bounds, we show that the problem of pattern recognition is significantly simpler than barcode decoding, as long as the minimum Hamming distance between images from different classes is large enough. Finally, we theoretically demonstrate the advantage of using quantum sensors for pattern recognition with the nearest neighbor classifier, a supervised learning algorithm, and numerically verify this prediction for handwritten digit classification.

Supervised Learning Enhanced by an Entangled Sensor Network

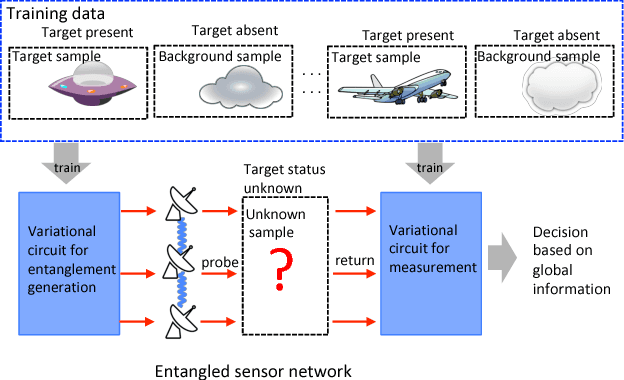
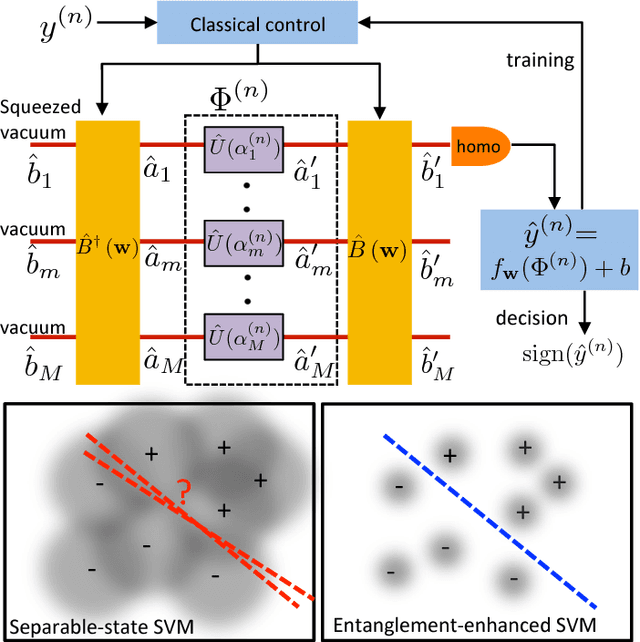
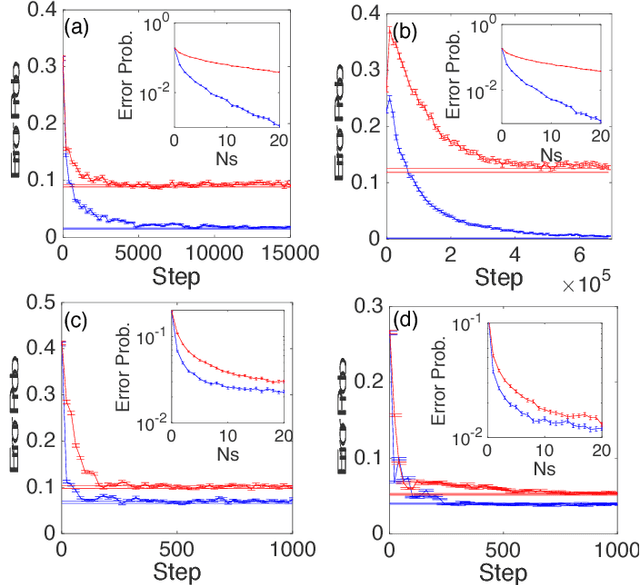
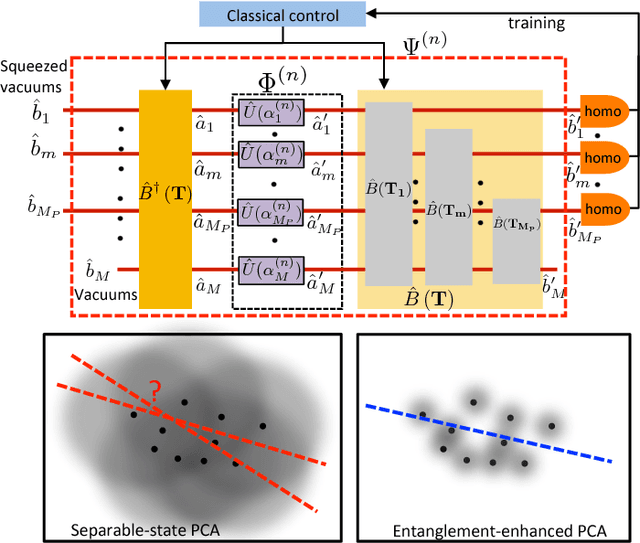
Various existing quantum supervised learning (SL) schemes rely on quantum random access memories to store quantum-encoded data given a priori in a classical description. The data acquisition process, however, has not been accounted for, while it sets the ultimate limit of the usefulness of the data for different SL tasks, as constrained by the quantum Cramer-Rao bound. We introduce supervised learning enhanced by an entangled sensor network (SLEEN) as a means to carry out SL tasks at the physical layer where a quantum advantage is achieved. The entanglement shared by different sensors boosts the performance of extracting global features of the object under investigation. We leverage SLEEN to construct an entanglement-enhanced support-vector machine for quantum data classification and entanglement-enhanced principal component analyzer for quantum data compression. In both schemes, variational circuits are employed to seek the optimum entangled probe state and measurement settings to maximize the entanglement-enabled quantum advantage. We compare the performance of SLEEN with separable-state SL schemes and observe an appreciable entanglement-enabled performance gain even in the presence of loss. SLEEN is realizable with available technology, opening a viable route toward building near-term quantum devices that offer unmatched performance beyond what the optimum classical device is able to afford.