GSON: A Group-based Social Navigation Framework with Large Multimodal Model

As the number of service robots and autonomous vehicles in human-centered environments grows, their requirements go beyond simply navigating to a destination. They must also take into account dynamic social contexts and ensure respect and comfort for others in shared spaces, which poses significant challenges for perception and planning. In this paper, we present a group-based social navigation framework GSON to enable mobile robots to perceive and exploit the social group of their surroundings by leveling the visual reasoning capability of the Large Multimodal Model (LMM). For perception, we apply visual prompting techniques to zero-shot extract the social relationship among pedestrians and combine the result with a robust pedestrian detection and tracking pipeline to alleviate the problem of low inference speed of the LMM. Given the perception result, the planning system is designed to avoid disrupting the current social structure. We adopt a social structure-based mid-level planner as a bridge between global path planning and local motion planning to preserve the global context and reactive response. The proposed method is validated on real-world mobile robot navigation tasks involving complex social structure understanding and reasoning. Experimental results demonstrate the effectiveness of the system in these scenarios compared with several baselines.

EmbSum: Leveraging the Summarization Capabilities of Large Language Models for Content-Based Recommendations

Content-based recommendation systems play a crucial role in delivering personalized content to users in the digital world. In this work, we introduce EmbSum, a novel framework that enables offline pre-computations of users and candidate items while capturing the interactions within the user engagement history. By utilizing the pretrained encoder-decoder model and poly-attention layers, EmbSum derives User Poly-Embedding (UPE) and Content Poly-Embedding (CPE) to calculate relevance scores between users and candidate items. EmbSum actively learns the long user engagement histories by generating user-interest summary with supervision from large language model (LLM). The effectiveness of EmbSum is validated on two datasets from different domains, surpassing state-of-the-art (SoTA) methods with higher accuracy and fewer parameters. Additionally, the model's ability to generate summaries of user interests serves as a valuable by-product, enhancing its usefulness for personalized content recommendations.

Minimax Regret Learning for Data with Heterogeneous Subgroups

Modern complex datasets often consist of various sub-populations. To develop robust and generalizable methods in the presence of sub-population heterogeneity, it is important to guarantee a uniform learning performance instead of an average one. In many applications, prior information is often available on which sub-population or group the data points belong to. Given the observed groups of data, we develop a min-max-regret (MMR) learning framework for general supervised learning, which targets to minimize the worst-group regret. Motivated from the regret-based decision theoretic framework, the proposed MMR is distinguished from the value-based or risk-based robust learning methods in the existing literature. The regret criterion features several robustness and invariance properties simultaneously. In terms of generalizability, we develop the theoretical guarantee for the worst-case regret over a super-population of the meta data, which incorporates the observed sub-populations, their mixtures, as well as other unseen sub-populations that could be approximated by the observed ones. We demonstrate the effectiveness of our method through extensive simulation studies and an application to kidney transplantation data from hundreds of transplant centers.

Fair Information Spread on Social Networks with Community Structure

Information spread through social networks is ubiquitous. Influence maximiza- tion (IM) algorithms aim to identify individuals who will generate the greatest spread through the social network if provided with information, and have been largely devel- oped with marketing in mind. In social networks with community structure, which are very common, IM algorithms focused solely on maximizing spread may yield signifi- cant disparities in information coverage between communities, which is problematic in settings such as public health messaging. While some IM algorithms aim to remedy disparity in information coverage using node attributes, none use the empirical com- munity structure within the network itself, which may be beneficial since communities directly affect the spread of information. Further, the use of empirical network struc- ture allows us to leverage community detection techniques, making it possible to run fair-aware algorithms when there are no relevant node attributes available, or when node attributes do not accurately capture network community structure. In contrast to other fair IM algorithms, this work relies on fitting a model to the social network which is then used to determine a seed allocation strategy for optimal fair information spread. We develop an algorithm to determine optimal seed allocations for expected fair coverage, defined through maximum entropy, provide some theoretical guarantees under appropriate conditions, and demonstrate its empirical accuracy on both simu- lated and real networks. Because this algorithm relies on a fitted network model and not on the network directly, it is well-suited for partially observed and noisy social networks.

Conformal Prediction for Network-Assisted Regression

An important problem in network analysis is predicting a node attribute using both network covariates, such as graph embedding coordinates or local subgraph counts, and conventional node covariates, such as demographic characteristics. While standard regression methods that make use of both types of covariates may be used for prediction, statistical inference is complicated by the fact that the nodal summary statistics are often dependent in complex ways. We show that under a mild joint exchangeability assumption, a network analog of conformal prediction achieves finite sample validity for a wide range of network covariates. We also show that a form of asymptotic conditional validity is achievable. The methods are illustrated on both simulated networks and a citation network dataset.

Variational Estimators of the Degree-corrected Latent Block Model for Bipartite Networks

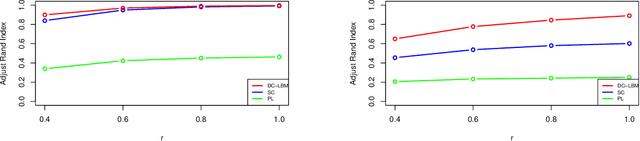
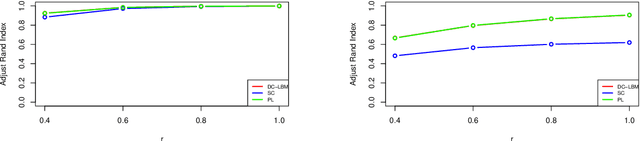
Biclustering on bipartite graphs is an unsupervised learning task that simultaneously clusters the two types of objects in the graph, for example, users and movies in a movie review dataset. The latent block model (LBM) has been proposed as a model-based tool for biclustering. Biclustering results by the LBM are, however, usually dominated by the row and column sums of the data matrix, i.e., degrees. We propose a degree-corrected latent block model (DC-LBM) to accommodate degree heterogeneity in row and column clusters, which greatly outperforms the classical LBM in the MovieLens dataset and simulated data. We develop an efficient variational expectation-maximization algorithm by observing that the row and column degrees maximize the objective function in the M step given any probability assignment on the cluster labels. We prove the label consistency of the variational estimator under the DC-LBM, which allows the expected graph density goes to zero as long as the average expected degrees of rows and columns go to infinity.

Latent space models for multiplex networks with shared structure

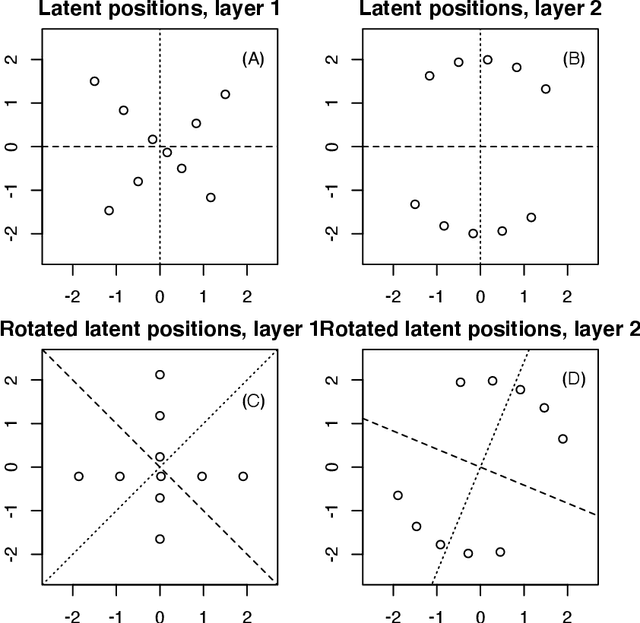
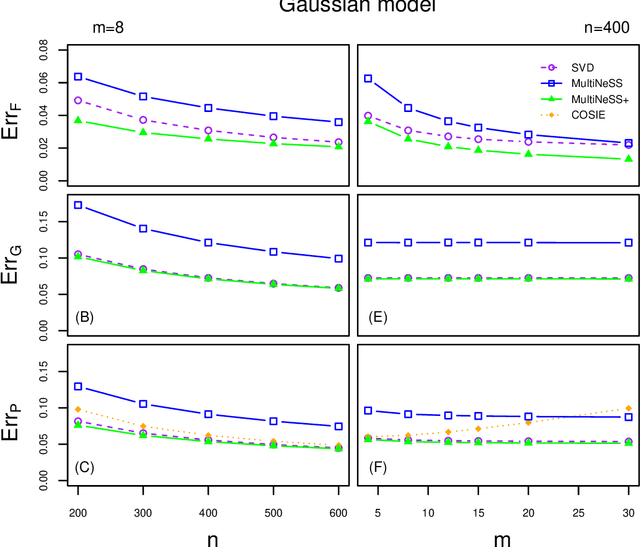
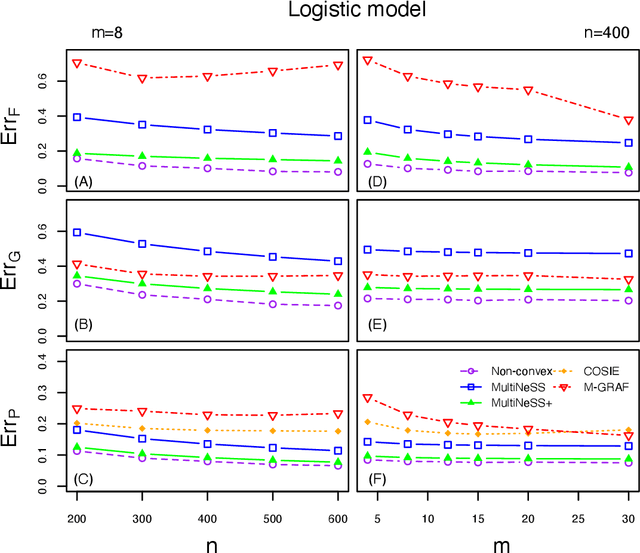
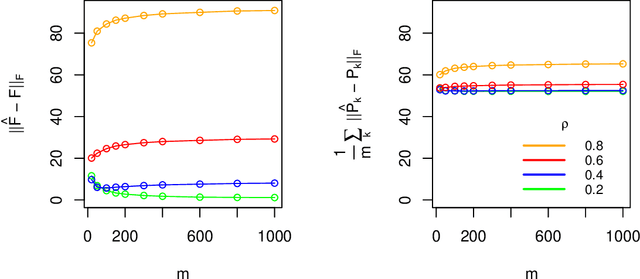
Latent space models are frequently used for modeling single-layer networks and include many popular special cases, such as the stochastic block model and the random dot product graph. However, they are not well-developed for more complex network structures, which are becoming increasingly common in practice. Here we propose a new latent space model for multiplex networks: multiple, heterogeneous networks observed on a shared node set. Multiplex networks can represent a network sample with shared node labels, a network evolving over time, or a network with multiple types of edges. The key feature of our model is that it learns from data how much of the network structure is shared between layers and pools information across layers as appropriate. We establish identifiability, develop a fitting procedure using convex optimization in combination with a nuclear norm penalty, and prove a guarantee of recovery for the latent positions as long as there is sufficient separation between the shared and the individual latent subspaces. We compare the model to competing methods in the literature on simulated networks and on a multiplex network describing the worldwide trade of agricultural products.

Fast Network Community Detection with Profile-Pseudo Likelihood Methods

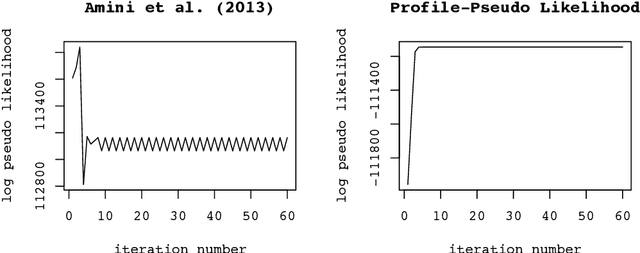
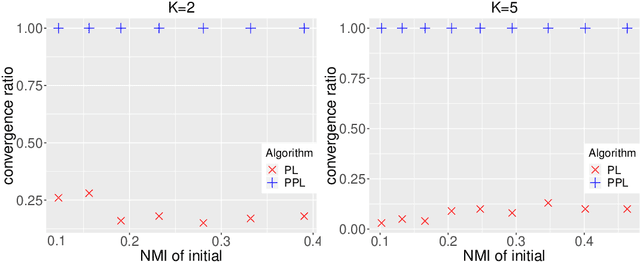
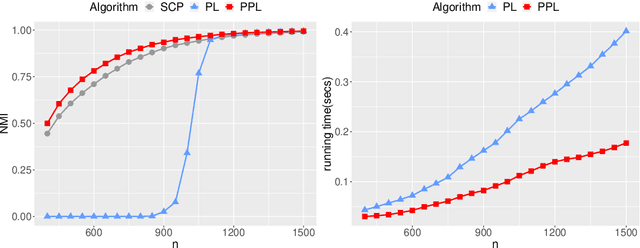
The stochastic block model is one of the most studied network models for community detection. It is well-known that most algorithms proposed for fitting the stochastic block model likelihood function cannot scale to large-scale networks. One prominent work that overcomes this computational challenge is Amini et al.(2013), which proposed a fast pseudo-likelihood approach for fitting stochastic block models to large sparse networks. However, this approach does not have convergence guarantee, and is not well suited for small- or medium- scale networks. In this article, we propose a novel likelihood based approach that decouples row and column labels in the likelihood function, which enables a fast alternating maximization; the new method is computationally efficient, performs well for both small and large scale networks, and has provable convergence guarantee. We show that our method provides strongly consistent estimates of the communities in a stochastic block model. As demonstrated in simulation studies, the proposed method outperforms the pseudo-likelihood approach in terms of both estimation accuracy and computation efficiency, especially for large sparse networks. We further consider extensions of our proposed method to handle networks with degree heterogeneity and bipartite properties.

SODEN: A Scalable Continuous-Time Survival Model through Ordinary Differential Equation Networks

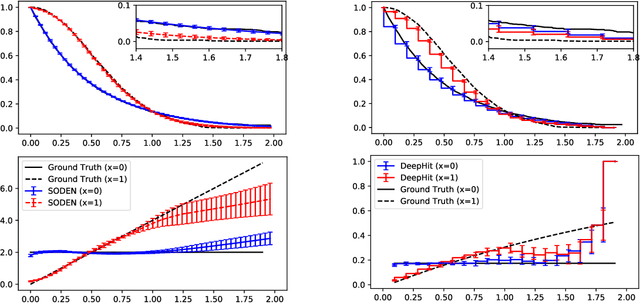
In this paper, we propose a flexible model for survival analysis using neural networks along with scalable optimization algorithms. One key technical challenge for directly applying maximum likelihood estimation (MLE) to censored data is that evaluating the objective function and its gradients with respect to model parameters requires the calculation of integrals. To address this challenge, we recognize that the MLE for censored data can be viewed as a differential-equation constrained optimization problem, a novel perspective. Following this connection, we model the distribution of event time through an ordinary differential equation and utilize efficient ODE solvers and adjoint sensitivity analysis to numerically evaluate the likelihood and the gradients. Using this approach, we are able to 1) provide a broad family of continuous-time survival distributions without strong structural assumptions, 2) obtain powerful feature representations using neural networks, and 3) allow efficient estimation of the model in large-scale applications using stochastic gradient descent. Through both simulation studies and real-world data examples, we demonstrate the effectiveness of the proposed method in comparison to existing state-of-the-art deep learning survival analysis models.

Community models for partially observed networks from surveys

Communities are a common and widely studied structure in networks, typically under the assumption that the network is fully and correctly observed. In practice, network data are often collected through sampling schemes such as surveys. These sampling mechanisms introduce noise and bias which can obscure the community structure and invalidate assumptions underlying standard community detection methods. We propose a general model for a class of network sampling mechanisms based on survey designs, designed to enable more accurate community detection for network data collected in this fashion. We model edge sampling probabilities as a function of both individual preferences and community parameters, and show community detection can be done by spectral clustering under this general class of models. We also propose, as a special case of the general framework, a parametric model for directed networks we call the nomination stochastic block model, which allows for meaningful parameter interpretations and can be fitted by the method of moments. Both spectral clustering and the method of moments in this case are computationally efficient and come with theoretical guarantees of consistency. We evaluate the proposed model in simulation studies on both unweighted and weighted networks and apply it to a faculty hiring dataset, discovering a meaningful hierarchy of communities among US business schools.