Strongly Consistent Community Detection in Popularity Adjusted Block Models

The Popularity Adjusted Block Model (PABM) provides a flexible framework for community detection in network data by allowing heterogeneous node popularity across communities. However, this flexibility increases model complexity and raises key unresolved challenges, particularly in effectively adapting spectral clustering techniques and efficiently achieving strong consistency in label recovery. To address these challenges, we first propose the Thresholded Cosine Spectral Clustering (TCSC) algorithm and establish its weak consistency under the PABM. We then introduce the one-step Refined TCSC algorithm and prove that it achieves strong consistency under the PABM, correctly recovering all community labels with high probability. We further show that the two-step Refined TCSC accelerates clustering error convergence, especially with small sample sizes. Additionally, we propose a data-driven approach for selecting the number of communities, which outperforms existing methods under the PABM. The effectiveness and robustness of our methods are validated through extensive simulations and real-world applications.

Fast Network Community Detection with Profile-Pseudo Likelihood Methods

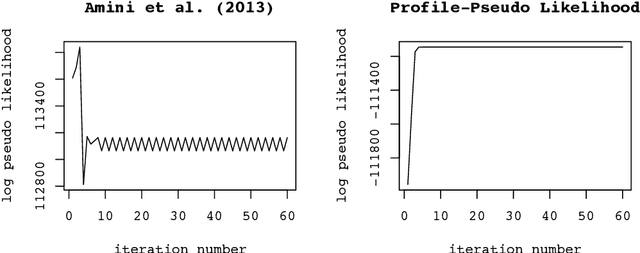
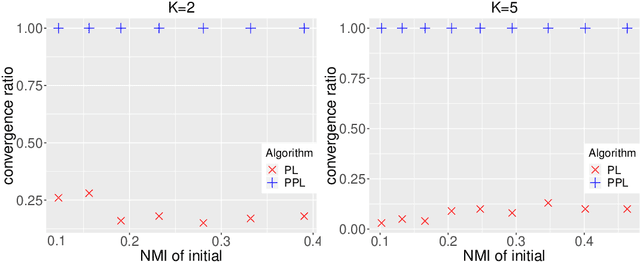
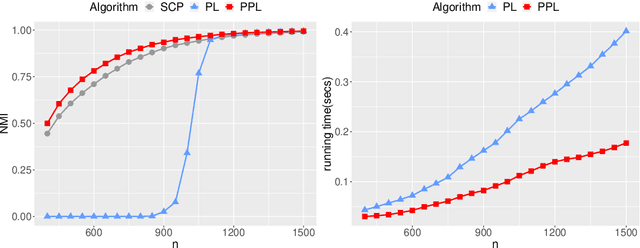
The stochastic block model is one of the most studied network models for community detection. It is well-known that most algorithms proposed for fitting the stochastic block model likelihood function cannot scale to large-scale networks. One prominent work that overcomes this computational challenge is Amini et al.(2013), which proposed a fast pseudo-likelihood approach for fitting stochastic block models to large sparse networks. However, this approach does not have convergence guarantee, and is not well suited for small- or medium- scale networks. In this article, we propose a novel likelihood based approach that decouples row and column labels in the likelihood function, which enables a fast alternating maximization; the new method is computationally efficient, performs well for both small and large scale networks, and has provable convergence guarantee. We show that our method provides strongly consistent estimates of the communities in a stochastic block model. As demonstrated in simulation studies, the proposed method outperforms the pseudo-likelihood approach in terms of both estimation accuracy and computation efficiency, especially for large sparse networks. We further consider extensions of our proposed method to handle networks with degree heterogeneity and bipartite properties.