Fair Information Spread on Social Networks with Community Structure

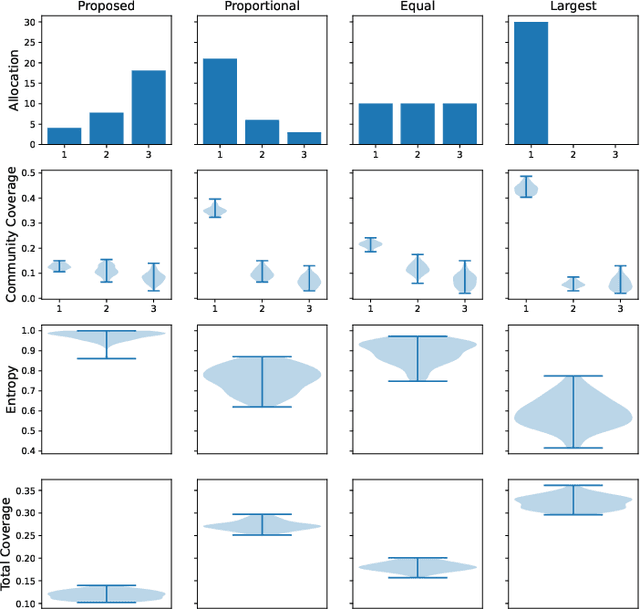
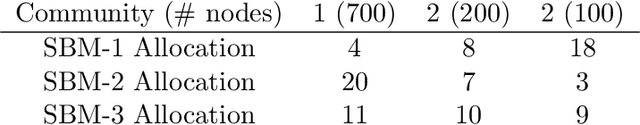
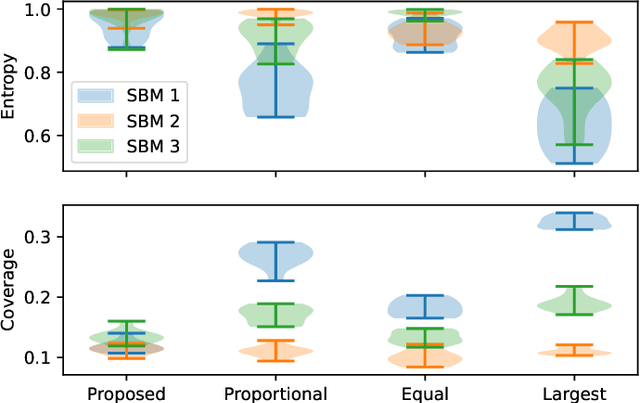
Information spread through social networks is ubiquitous. Influence maximiza- tion (IM) algorithms aim to identify individuals who will generate the greatest spread through the social network if provided with information, and have been largely devel- oped with marketing in mind. In social networks with community structure, which are very common, IM algorithms focused solely on maximizing spread may yield signifi- cant disparities in information coverage between communities, which is problematic in settings such as public health messaging. While some IM algorithms aim to remedy disparity in information coverage using node attributes, none use the empirical com- munity structure within the network itself, which may be beneficial since communities directly affect the spread of information. Further, the use of empirical network struc- ture allows us to leverage community detection techniques, making it possible to run fair-aware algorithms when there are no relevant node attributes available, or when node attributes do not accurately capture network community structure. In contrast to other fair IM algorithms, this work relies on fitting a model to the social network which is then used to determine a seed allocation strategy for optimal fair information spread. We develop an algorithm to determine optimal seed allocations for expected fair coverage, defined through maximum entropy, provide some theoretical guarantees under appropriate conditions, and demonstrate its empirical accuracy on both simu- lated and real networks. Because this algorithm relies on a fitted network model and not on the network directly, it is well-suited for partially observed and noisy social networks.

A pseudo-likelihood approach to community detection in weighted networks

Community structure is common in many real networks, with nodes clustered in groups sharing the same connections patterns. While many community detection methods have been developed for networks with binary edges, few of them are applicable to networks with weighted edges, which are common in practice. We propose a pseudo-likelihood community estimation algorithm derived under the weighted stochastic block model for networks with normally distributed edge weights, extending the pseudo-likelihood algorithm for binary networks, which offers some of the best combinations of accuracy and computational efficiency. We prove that the estimates obtained by the proposed method are consistent under the assumption of homogeneous networks, a weighted analogue of the planted partition model, and show that they work well in practice for both homogeneous and heterogeneous networks. We illustrate the method on simulated networks and on a fMRI dataset, where edge weights represent connectivity between brain regions and are expected to be close to normal in distribution by construction.

Conformal Prediction for Network-Assisted Regression

An important problem in network analysis is predicting a node attribute using both network covariates, such as graph embedding coordinates or local subgraph counts, and conventional node covariates, such as demographic characteristics. While standard regression methods that make use of both types of covariates may be used for prediction, statistical inference is complicated by the fact that the nodal summary statistics are often dependent in complex ways. We show that under a mild joint exchangeability assumption, a network analog of conformal prediction achieves finite sample validity for a wide range of network covariates. We also show that a form of asymptotic conditional validity is achievable. The methods are illustrated on both simulated networks and a citation network dataset.

Selective Inference for Sparse Multitask Regression with Applications in Neuroimaging

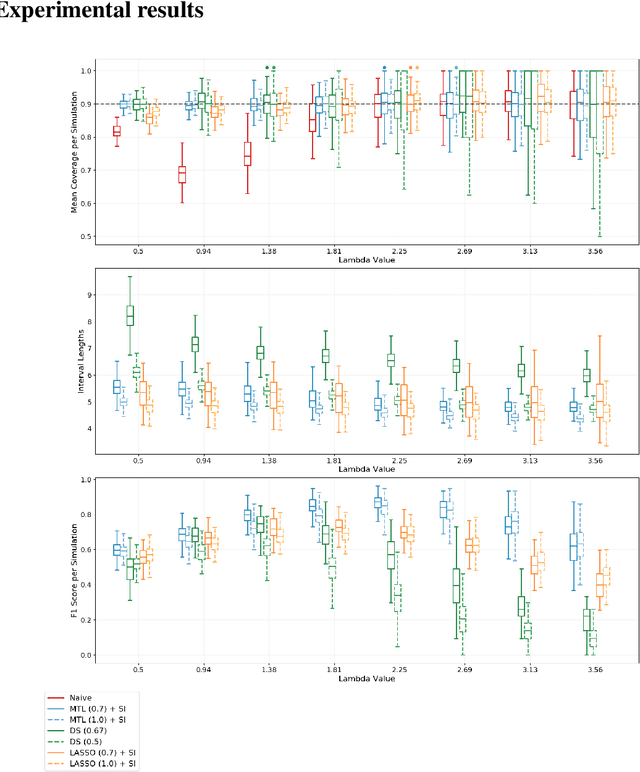
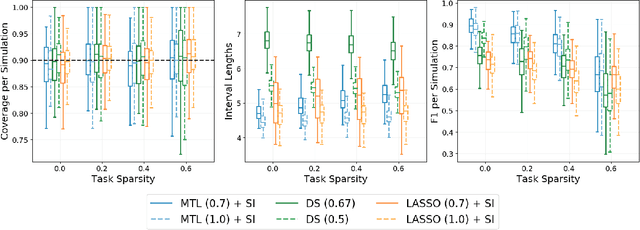
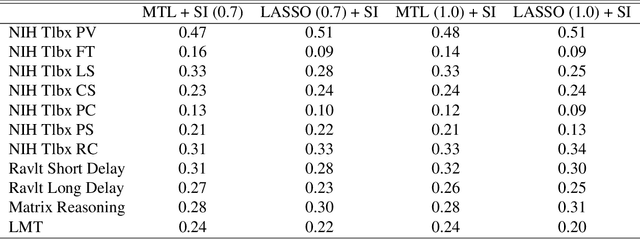
Multi-task learning is frequently used to model a set of related response variables from the same set of features, improving predictive performance and modeling accuracy relative to methods that handle each response variable separately. Despite the potential of multi-task learning to yield more powerful inference than single-task alternatives, prior work in this area has largely omitted uncertainty quantification. Our focus in this paper is a common multi-task problem in neuroimaging, where the goal is to understand the relationship between multiple cognitive task scores (or other subject-level assessments) and brain connectome data collected from imaging. We propose a framework for selective inference to address this problem, with the flexibility to: (i) jointly identify the relevant covariates for each task through a sparsity-inducing penalty, and (ii) conduct valid inference in a model based on the estimated sparsity structure. Our framework offers a new conditional procedure for inference, based on a refinement of the selection event that yields a tractable selection-adjusted likelihood. This gives an approximate system of estimating equations for maximum likelihood inference, solvable via a single convex optimization problem, and enables us to efficiently form confidence intervals with approximately the correct coverage. Applied to both simulated data and data from the Adolescent Cognitive Brain Development (ABCD) study, our selective inference methods yield tighter confidence intervals than commonly used alternatives, such as data splitting. We also demonstrate through simulations that multi-task learning with selective inference can more accurately recover true signals than single-task methods.

Latent space models for multiplex networks with shared structure

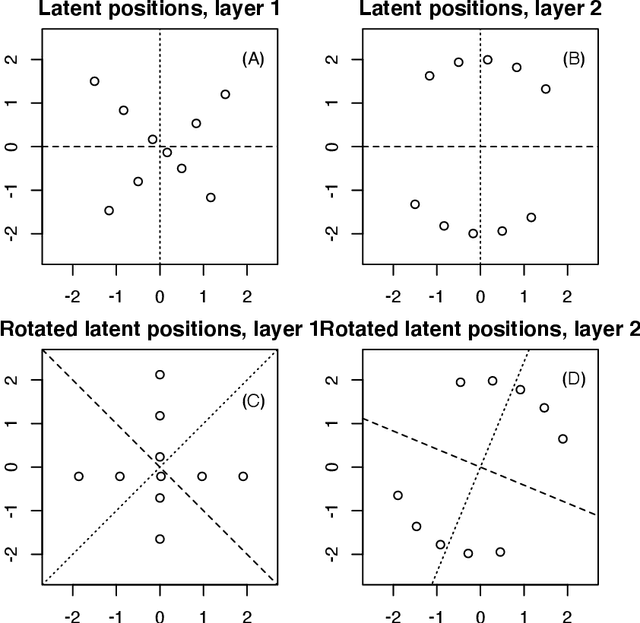
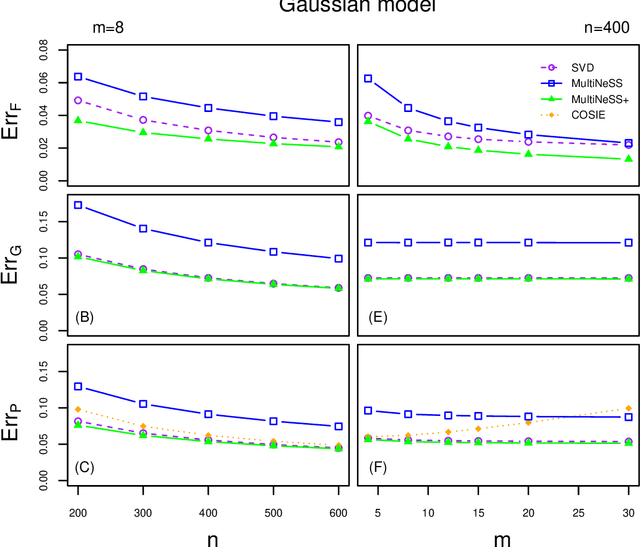
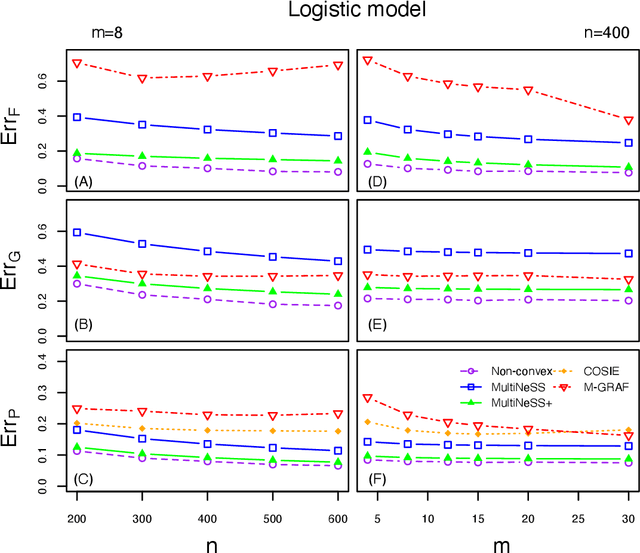
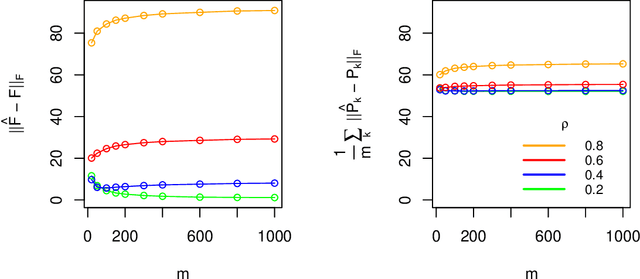
Latent space models are frequently used for modeling single-layer networks and include many popular special cases, such as the stochastic block model and the random dot product graph. However, they are not well-developed for more complex network structures, which are becoming increasingly common in practice. Here we propose a new latent space model for multiplex networks: multiple, heterogeneous networks observed on a shared node set. Multiplex networks can represent a network sample with shared node labels, a network evolving over time, or a network with multiple types of edges. The key feature of our model is that it learns from data how much of the network structure is shared between layers and pools information across layers as appropriate. We establish identifiability, develop a fitting procedure using convex optimization in combination with a nuclear norm penalty, and prove a guarantee of recovery for the latent positions as long as there is sufficient separation between the shared and the individual latent subspaces. We compare the model to competing methods in the literature on simulated networks and on a multiplex network describing the worldwide trade of agricultural products.

Overlapping community detection in networks via sparse spectral decomposition

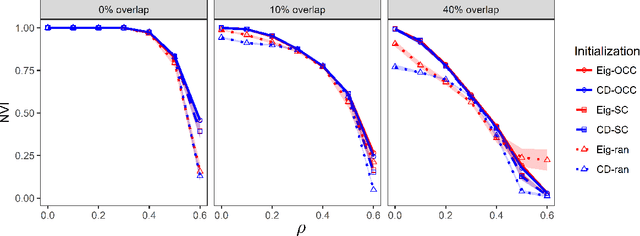
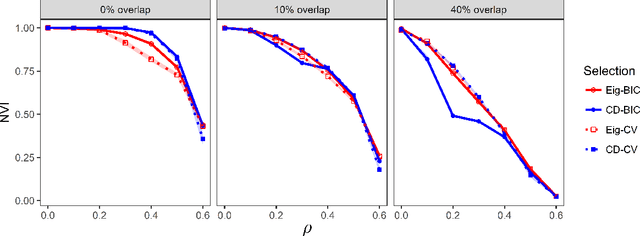
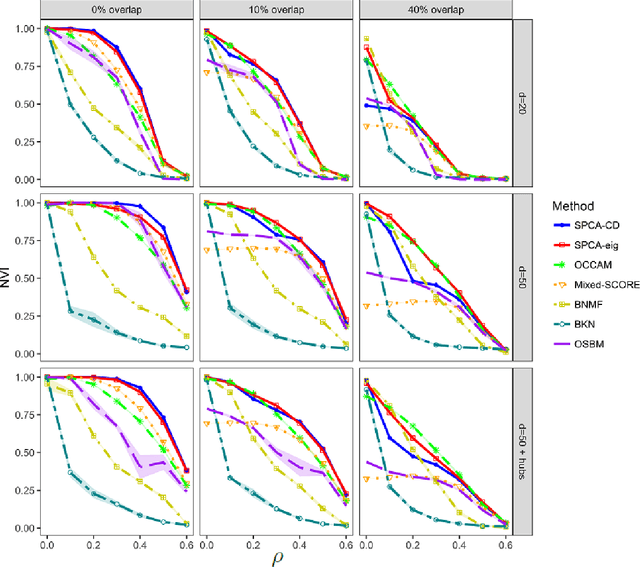
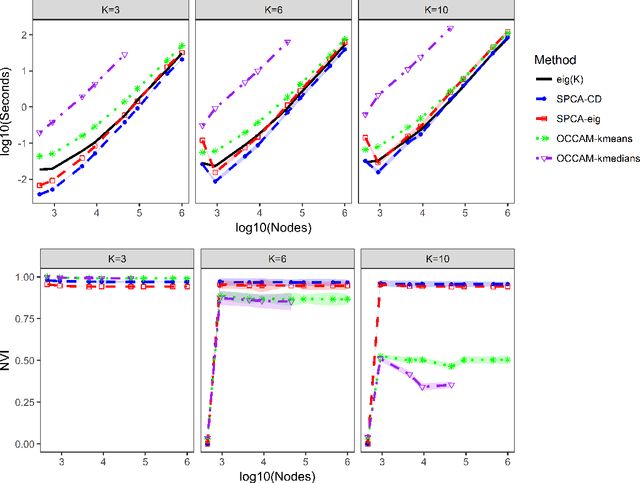
We consider the problem of estimating overlapping community memberships in a network, where each node can belong to multiple communities. More than a few communities per node are difficult to both estimate and interpret, so we focus on sparse node membership vectors. Our algorithm is based on sparse principal subspace estimation with iterative thresholding. The method is computationally efficient, with a computational cost equivalent to estimating the leading eigenvectors of the adjacency matrix, and does not require an additional clustering step, unlike spectral clustering methods. We show that a fixed point of the algorithm corresponds to correct node memberships under a version of the stochastic block model. The methods are evaluated empirically on simulated and real-world networks, showing good statistical performance and computational efficiency.

Community models for partially observed networks from surveys

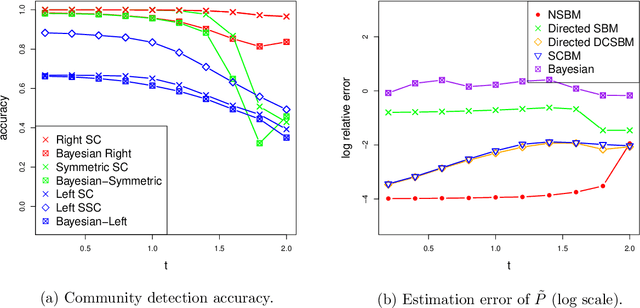
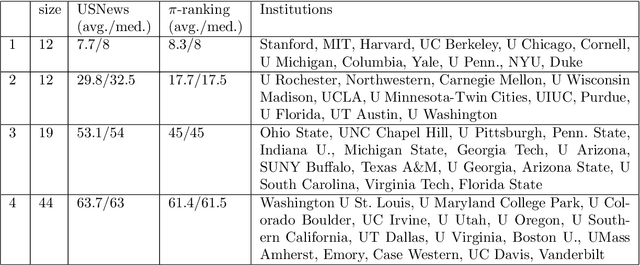
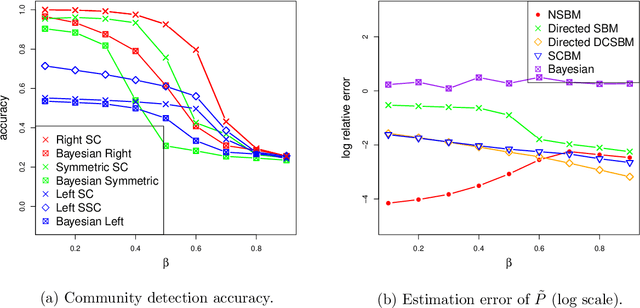
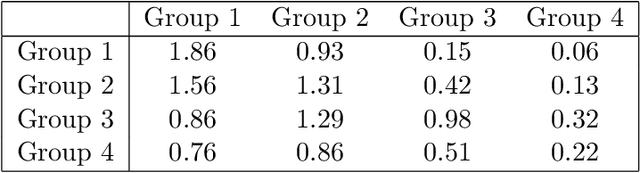
Communities are a common and widely studied structure in networks, typically under the assumption that the network is fully and correctly observed. In practice, network data are often collected through sampling schemes such as surveys. These sampling mechanisms introduce noise and bias which can obscure the community structure and invalidate assumptions underlying standard community detection methods. We propose a general model for a class of network sampling mechanisms based on survey designs, designed to enable more accurate community detection for network data collected in this fashion. We model edge sampling probabilities as a function of both individual preferences and community parameters, and show community detection can be done by spectral clustering under this general class of models. We also propose, as a special case of the general framework, a parametric model for directed networks we call the nomination stochastic block model, which allows for meaningful parameter interpretations and can be fitted by the method of moments. Both spectral clustering and the method of moments in this case are computationally efficient and come with theoretical guarantees of consistency. We evaluate the proposed model in simulation studies on both unweighted and weighted networks and apply it to a faculty hiring dataset, discovering a meaningful hierarchy of communities among US business schools.

Simultaneous prediction and community detection for networks with application to neuroimaging

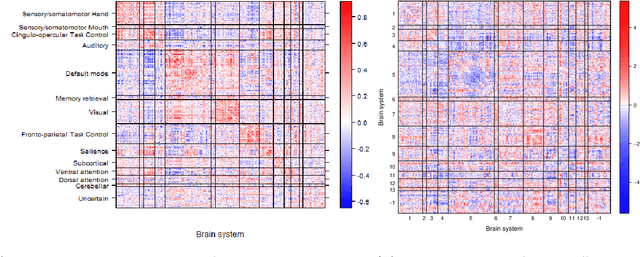
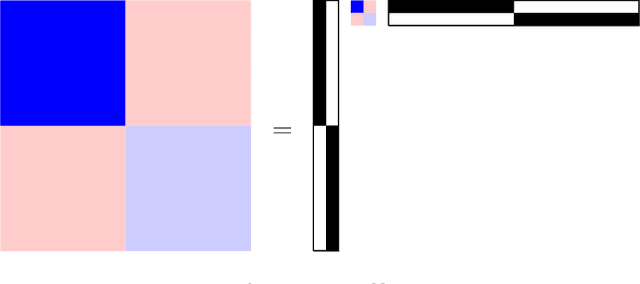
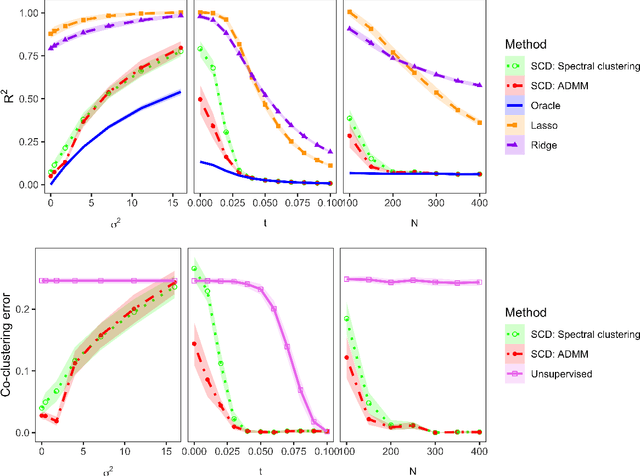
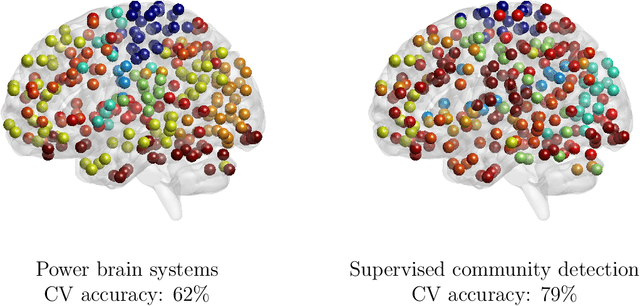
Community structure in networks is observed in many different domains, and unsupervised community detection has received a lot of attention in the literature. Increasingly the focus of network analysis is shifting towards using network information in some other prediction or inference task rather than just analyzing the network itself. In particular, in neuroimaging applications brain networks are available for multiple subjects and the goal is often to predict a phenotype of interest. Community structure is well known to be a feature of brain networks, typically corresponding to different regions of the brain responsible for different functions. There are standard parcellations of the brain into such regions, usually obtained by applying clustering methods to brain connectomes of healthy subjects. However, when the goal is predicting a phenotype or distinguishing between different conditions, these static communities from an unrelated set of healthy subjects may not be the most useful for prediction. Here we present a method for supervised community detection, aiming to find a partition of the network into communities that is most useful for predicting a particular response. We use a block-structured regularization penalty combined with a prediction loss function, and compute the solution with a combination of a spectral method and an ADMM optimization algorithm. We show that the spectral clustering method recovers the correct communities under a weighted stochastic block model. The method performs well on both simulated and real brain networks, providing support for the idea of task-dependent brain regions.

High-dimensional Gaussian graphical model for network-linked data

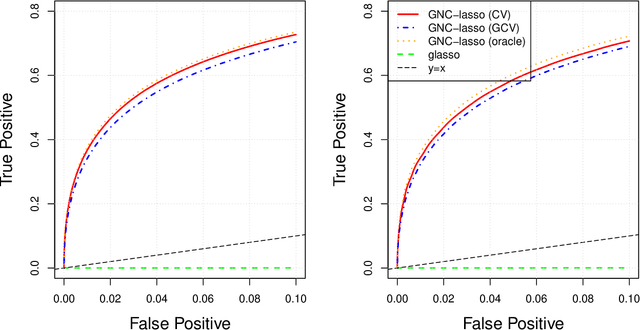
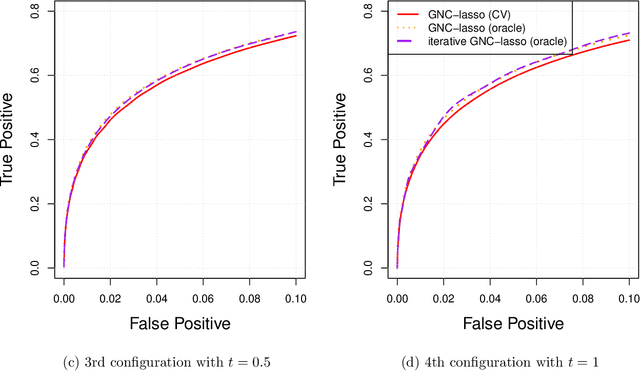
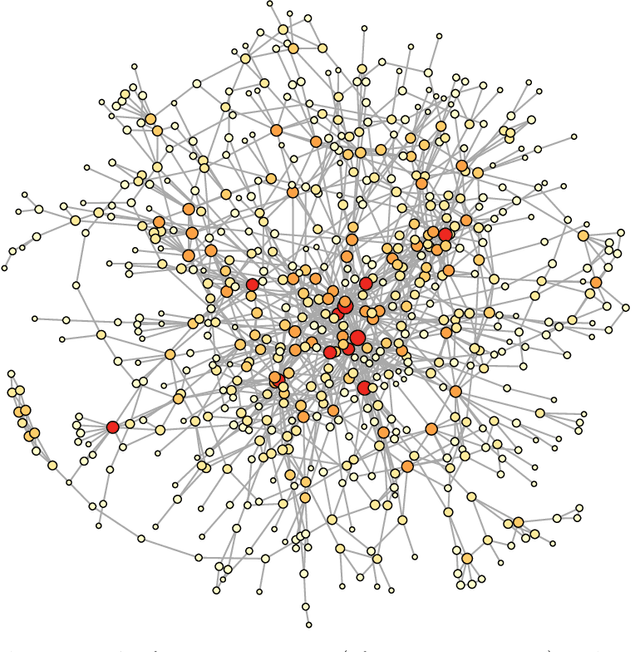
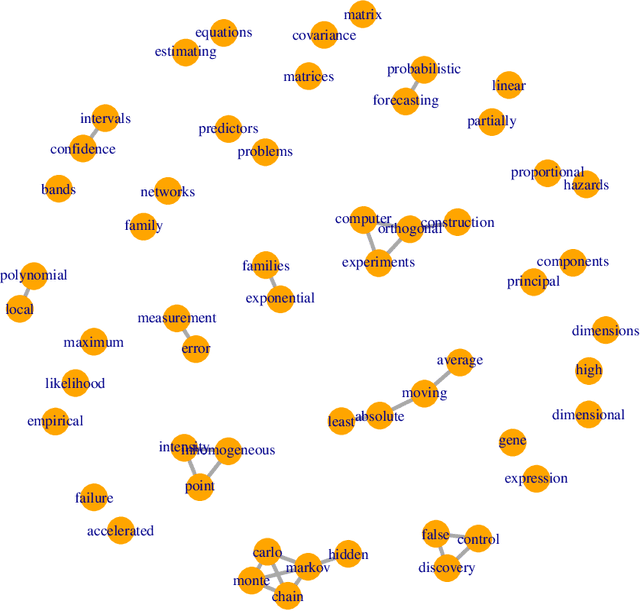
Graphical models are commonly used to represent conditional dependence relationships between variables. There are multiple methods available for exploring them from high-dimensional data, but almost all of them rely on the assumption that the observations are independent and identically distributed. At the same time, observations connected by a network are becoming increasingly common, and tend to violate these assumptions. Here we develop a Gaussian graphical model for observations connected by a network with potentially different mean vectors, varying smoothly over the network. We propose an efficient estimation algorithm and demonstrate its effectiveness on both simulated and real data, obtaining meaningful interpretable results on a statistics coauthorship network. We also prove that our method estimates both the inverse covariance matrix and the corresponding graph structure correctly under the assumption of network "cohesion", which refers to the empirically observed phenomenon of network neighbors sharing similar traits.

Recovering low-rank structure from multiple networks with unknown edge distributions

In increasingly many settings, particularly in neuroimaging, data sets consist of multiple samples from a population of networks, with vertices aligned across networks. For example, fMRI studies yield graphs whose vertices correspond to brain regions, which are the same across subjects. We consider the setting where we observe a sample of networks whose adjacency matrices have a shared low-rank expectation, but edge-level noise distributions may vary from one network to another. We show that so long as edge noise is sub-gamma distributed in each network, the shared low-rank structure can be recovered accurately using an eigenvalue truncation of a weighted network average. We also explore the extent to which edge-level errors influence estimation and downstream inference tasks. The proposed approach is illustrated on synthetic networks and on an fMRI study of schizophrenia.