Ivo Danihelka
Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context
Mar 08, 2024Abstract:In this report, we present the latest model of the Gemini family, Gemini 1.5 Pro, a highly compute-efficient multimodal mixture-of-experts model capable of recalling and reasoning over fine-grained information from millions of tokens of context, including multiple long documents and hours of video and audio. Gemini 1.5 Pro achieves near-perfect recall on long-context retrieval tasks across modalities, improves the state-of-the-art in long-document QA, long-video QA and long-context ASR, and matches or surpasses Gemini 1.0 Ultra's state-of-the-art performance across a broad set of benchmarks. Studying the limits of Gemini 1.5 Pro's long-context ability, we find continued improvement in next-token prediction and near-perfect retrieval (>99%) up to at least 10M tokens, a generational leap over existing models such as Claude 2.1 (200k) and GPT-4 Turbo (128k). Finally, we highlight surprising new capabilities of large language models at the frontier; when given a grammar manual for Kalamang, a language with fewer than 200 speakers worldwide, the model learns to translate English to Kalamang at a similar level to a person who learned from the same content.
Gemini: A Family of Highly Capable Multimodal Models
Dec 19, 2023Abstract:This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.
Muesli: Combining Improvements in Policy Optimization
Apr 13, 2021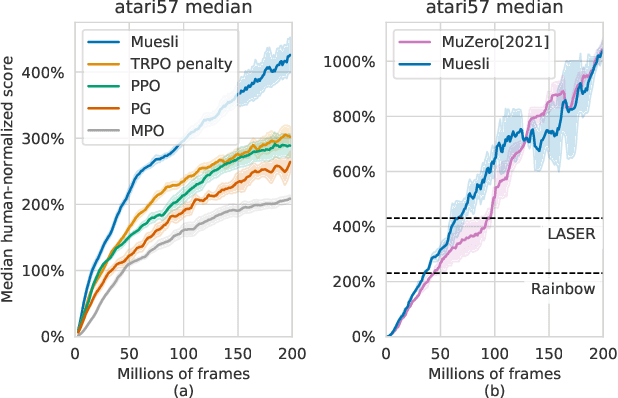
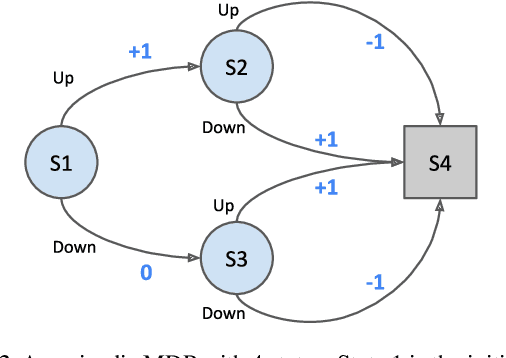
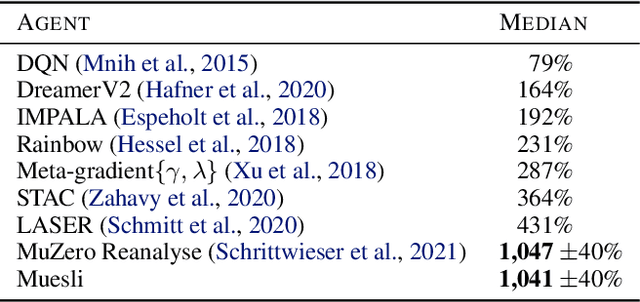
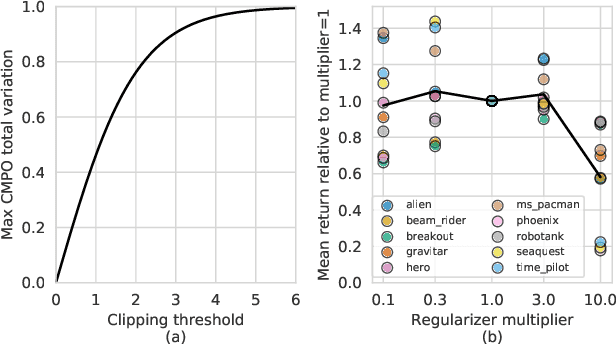
Abstract:We propose a novel policy update that combines regularized policy optimization with model learning as an auxiliary loss. The update (henceforth Muesli) matches MuZero's state-of-the-art performance on Atari. Notably, Muesli does so without using deep search: it acts directly with a policy network and has computation speed comparable to model-free baselines. The Atari results are complemented by extensive ablations, and by additional results on continuous control and 9x9 Go.
Causally Correct Partial Models for Reinforcement Learning
Feb 07, 2020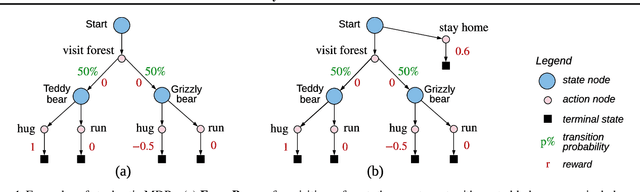


Abstract:In reinforcement learning, we can learn a model of future observations and rewards, and use it to plan the agent's next actions. However, jointly modeling future observations can be computationally expensive or even intractable if the observations are high-dimensional (e.g. images). For this reason, previous works have considered partial models, which model only part of the observation. In this paper, we show that partial models can be causally incorrect: they are confounded by the observations they don't model, and can therefore lead to incorrect planning. To address this, we introduce a general family of partial models that are provably causally correct, yet remain fast because they do not need to fully model future observations.
OpenSpiel: A Framework for Reinforcement Learning in Games
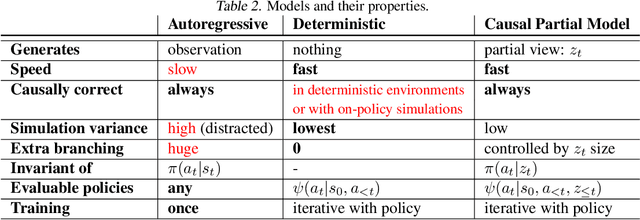
Oct 10, 2019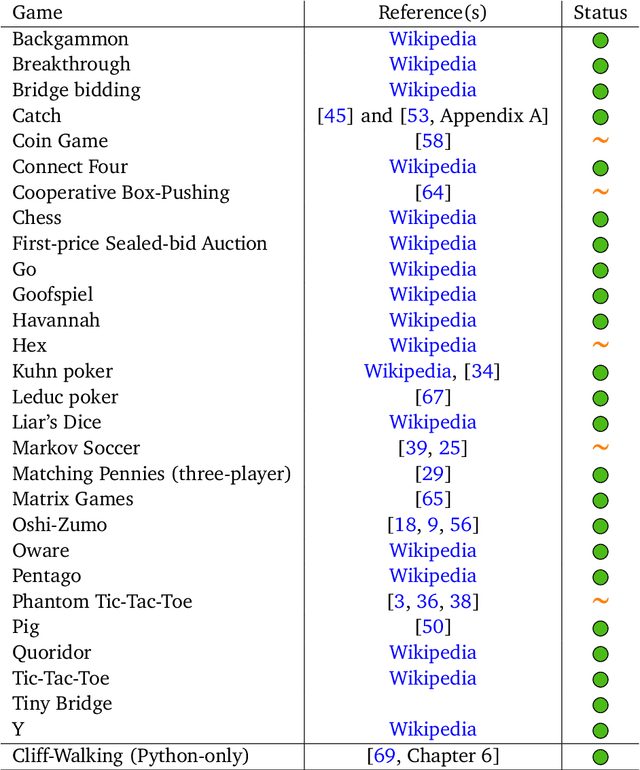
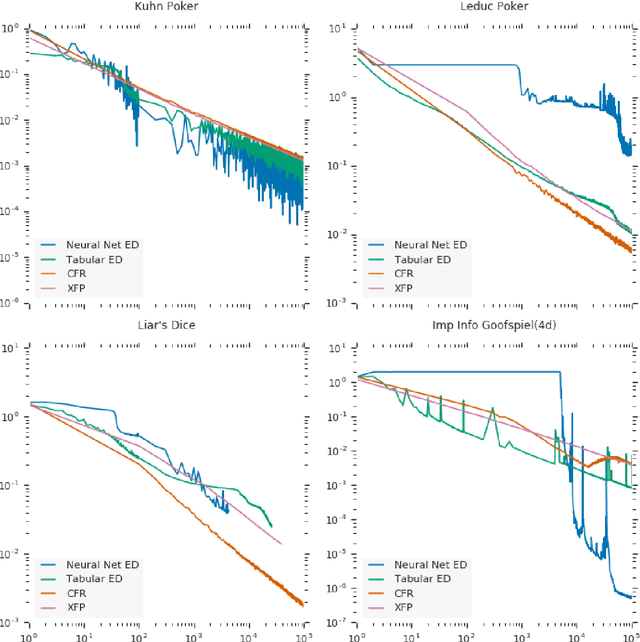
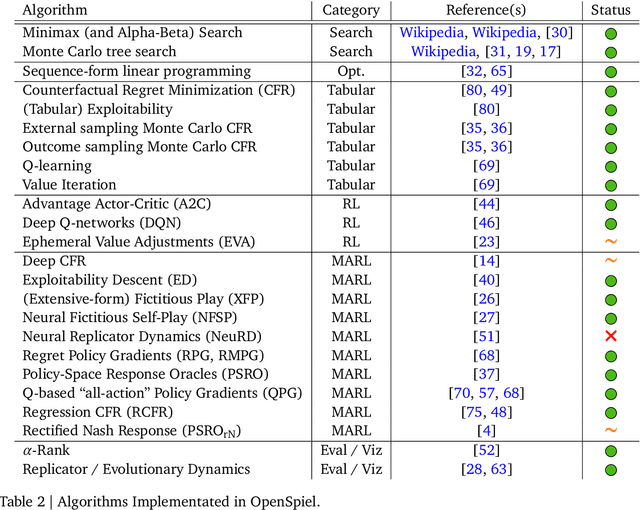
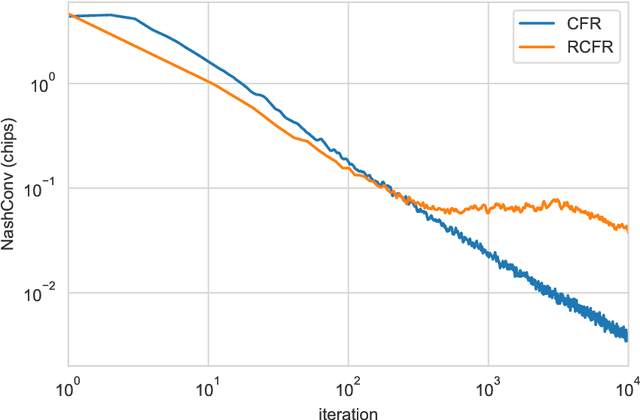
Abstract:OpenSpiel is a collection of environments and algorithms for research in general reinforcement learning and search/planning in games. OpenSpiel supports n-player (single- and multi- agent) zero-sum, cooperative and general-sum, one-shot and sequential, strictly turn-taking and simultaneous-move, perfect and imperfect information games, as well as traditional multiagent environments such as (partially- and fully- observable) grid worlds and social dilemmas. OpenSpiel also includes tools to analyze learning dynamics and other common evaluation metrics. This document serves both as an overview of the code base and an introduction to the terminology, core concepts, and algorithms across the fields of reinforcement learning, computational game theory, and search.
The Cramer Distance as a Solution to Biased Wasserstein Gradients
May 30, 2017
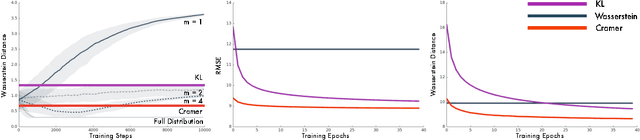

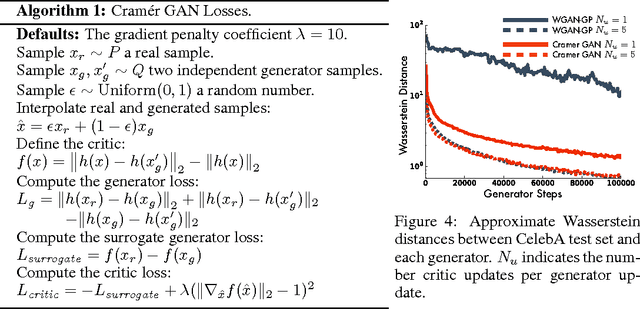
Abstract:The Wasserstein probability metric has received much attention from the machine learning community. Unlike the Kullback-Leibler divergence, which strictly measures change in probability, the Wasserstein metric reflects the underlying geometry between outcomes. The value of being sensitive to this geometry has been demonstrated, among others, in ordinal regression and generative modelling. In this paper we describe three natural properties of probability divergences that reflect requirements from machine learning: sum invariance, scale sensitivity, and unbiased sample gradients. The Wasserstein metric possesses the first two properties but, unlike the Kullback-Leibler divergence, does not possess the third. We provide empirical evidence suggesting that this is a serious issue in practice. Leveraging insights from probabilistic forecasting we propose an alternative to the Wasserstein metric, the Cram\'er distance. We show that the Cram\'er distance possesses all three desired properties, combining the best of the Wasserstein and Kullback-Leibler divergences. To illustrate the relevance of the Cram\'er distance in practice we design a new algorithm, the Cram\'er Generative Adversarial Network (GAN), and show that it performs significantly better than the related Wasserstein GAN.
Comparison of Maximum Likelihood and GAN-based training of Real NVPs
May 15, 2017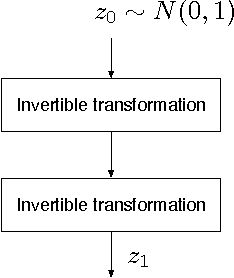


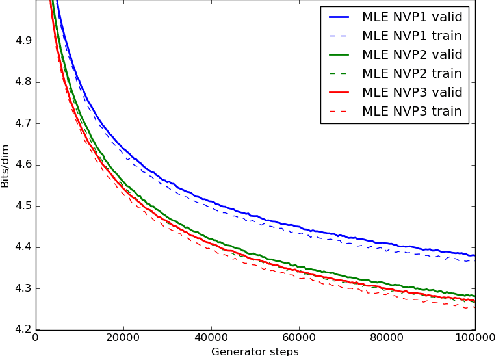
Abstract:We train a generator by maximum likelihood and we also train the same generator architecture by Wasserstein GAN. We then compare the generated samples, exact log-probability densities and approximate Wasserstein distances. We show that an independent critic trained to approximate Wasserstein distance between the validation set and the generator distribution helps detect overfitting. Finally, we use ideas from the one-shot learning literature to develop a novel fast learning critic.
Scaling Memory-Augmented Neural Networks with Sparse Reads and Writes
Oct 27, 2016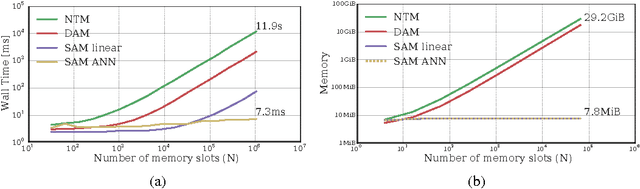
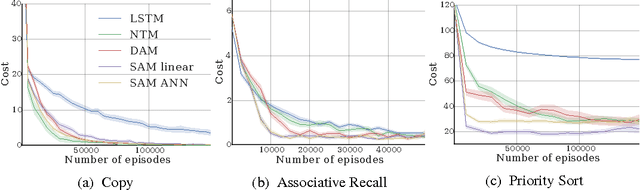
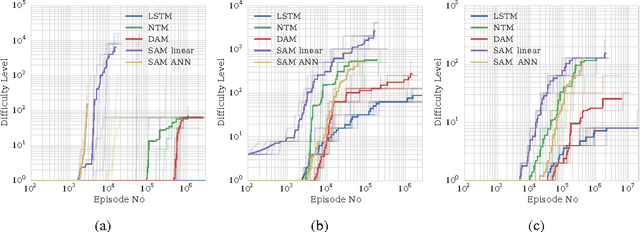
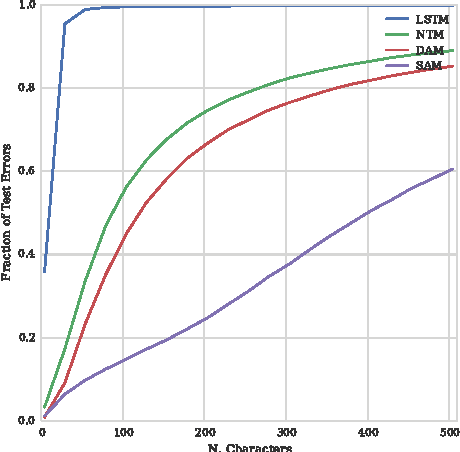
Abstract:Neural networks augmented with external memory have the ability to learn algorithmic solutions to complex tasks. These models appear promising for applications such as language modeling and machine translation. However, they scale poorly in both space and time as the amount of memory grows --- limiting their applicability to real-world domains. Here, we present an end-to-end differentiable memory access scheme, which we call Sparse Access Memory (SAM), that retains the representational power of the original approaches whilst training efficiently with very large memories. We show that SAM achieves asymptotic lower bounds in space and time complexity, and find that an implementation runs $1,\!000\times$ faster and with $3,\!000\times$ less physical memory than non-sparse models. SAM learns with comparable data efficiency to existing models on a range of synthetic tasks and one-shot Omniglot character recognition, and can scale to tasks requiring $100,\!000$s of time steps and memories. As well, we show how our approach can be adapted for models that maintain temporal associations between memories, as with the recently introduced Differentiable Neural Computer.
Video Pixel Networks
Oct 03, 2016
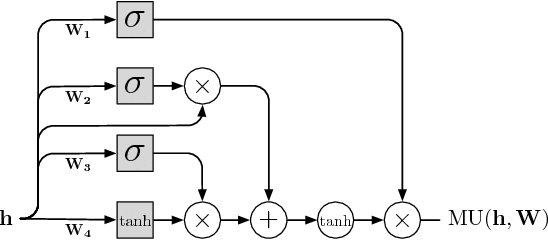


Abstract:We propose a probabilistic video model, the Video Pixel Network (VPN), that estimates the discrete joint distribution of the raw pixel values in a video. The model and the neural architecture reflect the time, space and color structure of video tensors and encode it as a four-dimensional dependency chain. The VPN approaches the best possible performance on the Moving MNIST benchmark, a leap over the previous state of the art, and the generated videos show only minor deviations from the ground truth. The VPN also produces detailed samples on the action-conditional Robotic Pushing benchmark and generalizes to the motion of novel objects.
Memory-Efficient Backpropagation Through Time
Jun 10, 2016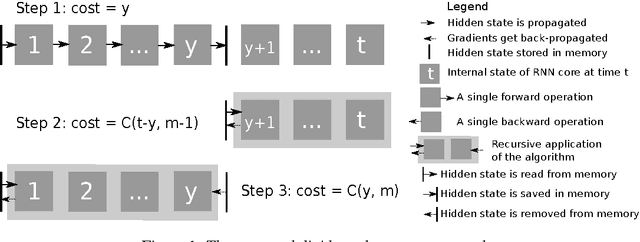
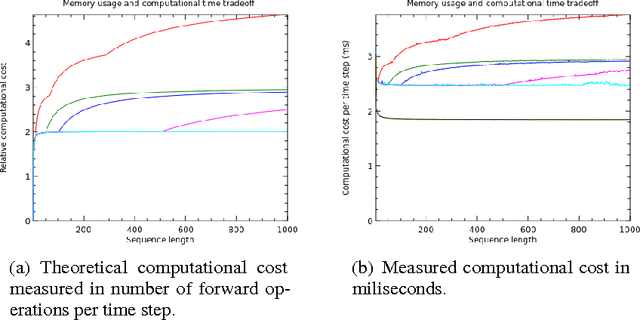
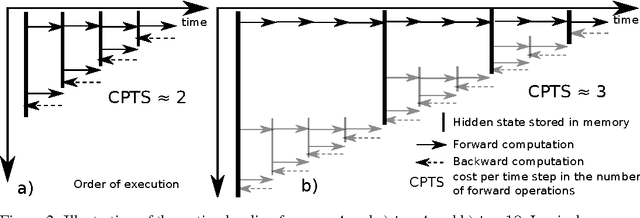
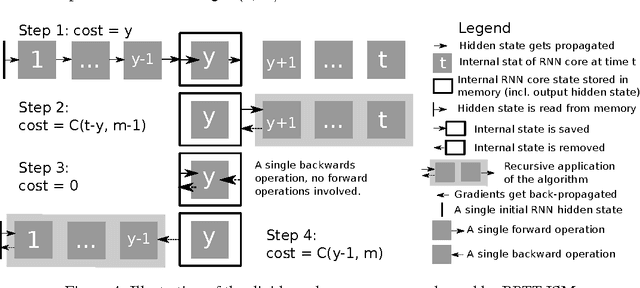
Abstract:We propose a novel approach to reduce memory consumption of the backpropagation through time (BPTT) algorithm when training recurrent neural networks (RNNs). Our approach uses dynamic programming to balance a trade-off between caching of intermediate results and recomputation. The algorithm is capable of tightly fitting within almost any user-set memory budget while finding an optimal execution policy minimizing the computational cost. Computational devices have limited memory capacity and maximizing a computational performance given a fixed memory budget is a practical use-case. We provide asymptotic computational upper bounds for various regimes. The algorithm is particularly effective for long sequences. For sequences of length 1000, our algorithm saves 95\% of memory usage while using only one third more time per iteration than the standard BPTT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge