David Silver
University College London
DataRater: Meta-Learned Dataset Curation
May 23, 2025Abstract:The quality of foundation models depends heavily on their training data. Consequently, great efforts have been put into dataset curation. Yet most approaches rely on manual tuning of coarse-grained mixtures of large buckets of data, or filtering by hand-crafted heuristics. An approach that is ultimately more scalable (let alone more satisfying) is to \emph{learn} which data is actually valuable for training. This type of meta-learning could allow more sophisticated, fine-grained, and effective curation. Our proposed \emph{DataRater} is an instance of this idea. It estimates the value of training on any particular data point. This is done by meta-learning using `meta-gradients', with the objective of improving training efficiency on held out data. In extensive experiments across a range of model scales and datasets, we find that using our DataRater to filter data is highly effective, resulting in significantly improved compute efficiency.
Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context
Mar 08, 2024Abstract:In this report, we present the latest model of the Gemini family, Gemini 1.5 Pro, a highly compute-efficient multimodal mixture-of-experts model capable of recalling and reasoning over fine-grained information from millions of tokens of context, including multiple long documents and hours of video and audio. Gemini 1.5 Pro achieves near-perfect recall on long-context retrieval tasks across modalities, improves the state-of-the-art in long-document QA, long-video QA and long-context ASR, and matches or surpasses Gemini 1.0 Ultra's state-of-the-art performance across a broad set of benchmarks. Studying the limits of Gemini 1.5 Pro's long-context ability, we find continued improvement in next-token prediction and near-perfect retrieval (>99%) up to at least 10M tokens, a generational leap over existing models such as Claude 2.1 (200k) and GPT-4 Turbo (128k). Finally, we highlight surprising new capabilities of large language models at the frontier; when given a grammar manual for Kalamang, a language with fewer than 200 speakers worldwide, the model learns to translate English to Kalamang at a similar level to a person who learned from the same content.
Gemini: A Family of Highly Capable Multimodal Models
Dec 19, 2023Abstract:This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.
Mastering the Game of Stratego with Model-Free Multiagent Reinforcement Learning
Jun 30, 2022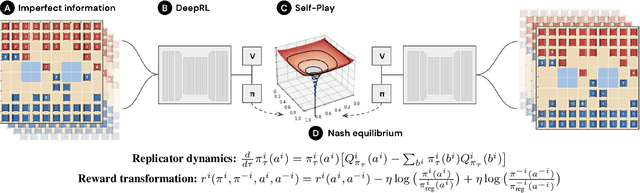
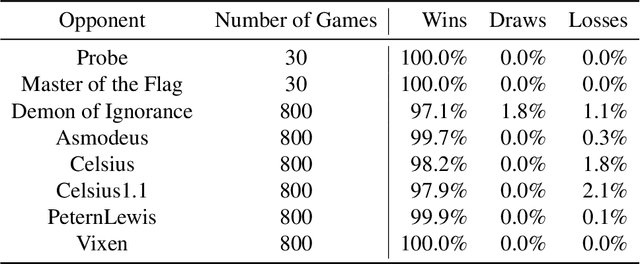
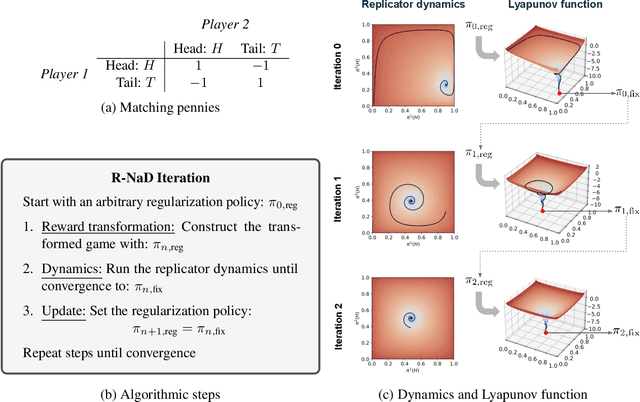

Abstract:We introduce DeepNash, an autonomous agent capable of learning to play the imperfect information game Stratego from scratch, up to a human expert level. Stratego is one of the few iconic board games that Artificial Intelligence (AI) has not yet mastered. This popular game has an enormous game tree on the order of $10^{535}$ nodes, i.e., $10^{175}$ times larger than that of Go. It has the additional complexity of requiring decision-making under imperfect information, similar to Texas hold'em poker, which has a significantly smaller game tree (on the order of $10^{164}$ nodes). Decisions in Stratego are made over a large number of discrete actions with no obvious link between action and outcome. Episodes are long, with often hundreds of moves before a player wins, and situations in Stratego can not easily be broken down into manageably-sized sub-problems as in poker. For these reasons, Stratego has been a grand challenge for the field of AI for decades, and existing AI methods barely reach an amateur level of play. DeepNash uses a game-theoretic, model-free deep reinforcement learning method, without search, that learns to master Stratego via self-play. The Regularised Nash Dynamics (R-NaD) algorithm, a key component of DeepNash, converges to an approximate Nash equilibrium, instead of 'cycling' around it, by directly modifying the underlying multi-agent learning dynamics. DeepNash beats existing state-of-the-art AI methods in Stratego and achieved a yearly (2022) and all-time top-3 rank on the Gravon games platform, competing with human expert players.
Self-Consistent Models and Values
Oct 25, 2021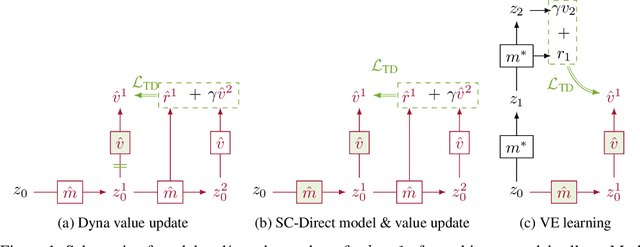

Abstract:Learned models of the environment provide reinforcement learning (RL) agents with flexible ways of making predictions about the environment. In particular, models enable planning, i.e. using more computation to improve value functions or policies, without requiring additional environment interactions. In this work, we investigate a way of augmenting model-based RL, by additionally encouraging a learned model and value function to be jointly \emph{self-consistent}. Our approach differs from classic planning methods such as Dyna, which only update values to be consistent with the model. We propose multiple self-consistency updates, evaluate these in both tabular and function approximation settings, and find that, with appropriate choices, self-consistency helps both policy evaluation and control.
Bootstrapped Meta-Learning
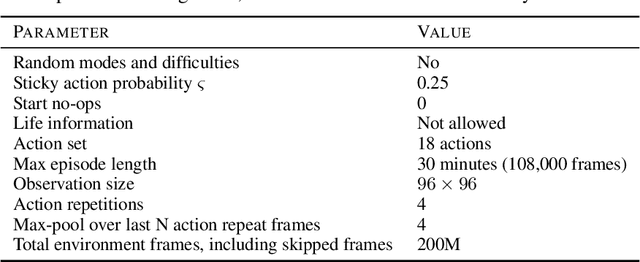
Sep 09, 2021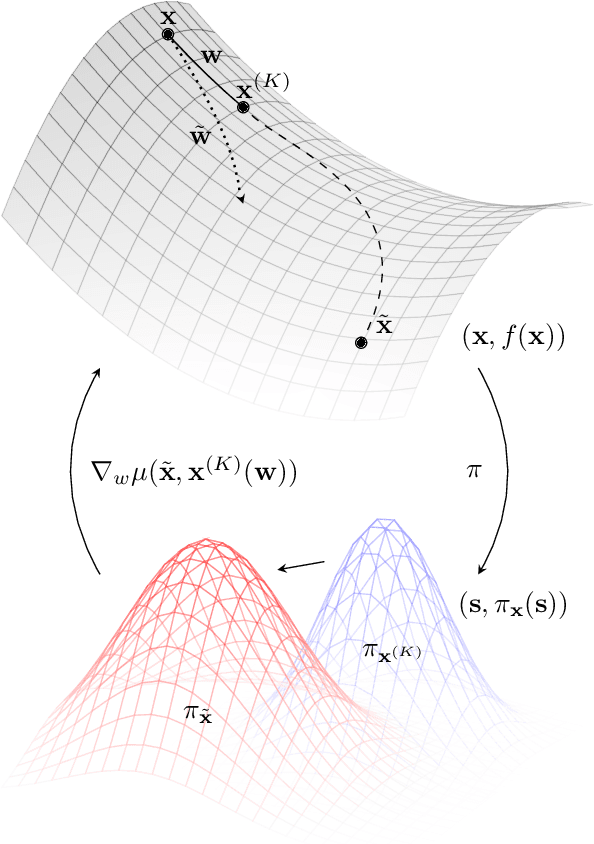

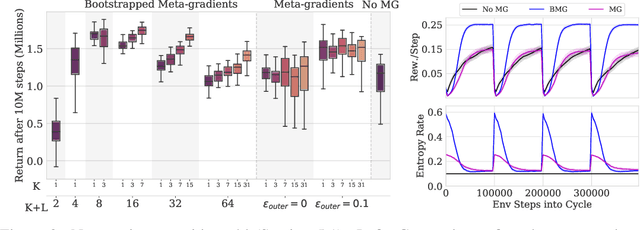
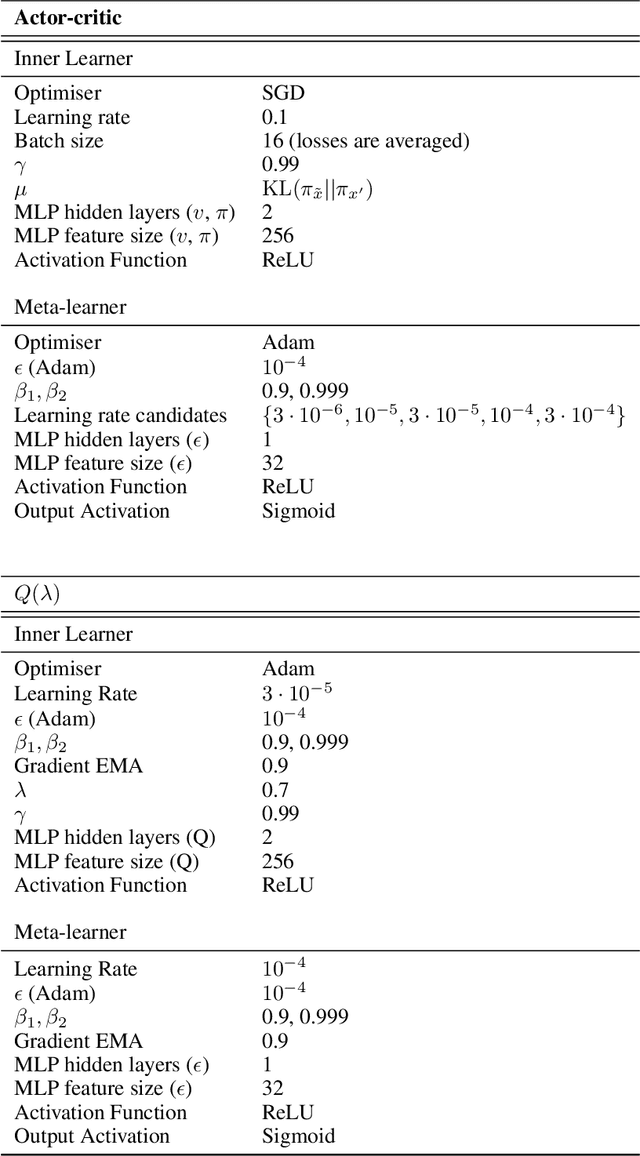
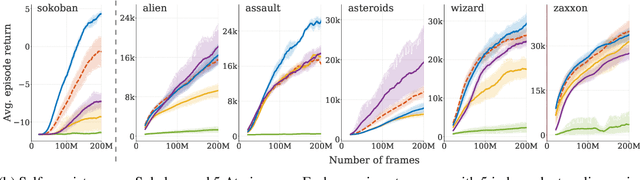
Abstract:Meta-learning empowers artificial intelligence to increase its efficiency by learning how to learn. Unlocking this potential involves overcoming a challenging meta-optimisation problem that often exhibits ill-conditioning, and myopic meta-objectives. We propose an algorithm that tackles these issues by letting the meta-learner teach itself. The algorithm first bootstraps a target from the meta-learner, then optimises the meta-learner by minimising the distance to that target under a chosen (pseudo-)metric. Focusing on meta-learning with gradients, we establish conditions that guarantee performance improvements and show that the improvement is related to the target distance. Thus, by controlling curvature, the distance measure can be used to ease meta-optimization, for instance by reducing ill-conditioning. Further, the bootstrapping mechanism can extend the effective meta-learning horizon without requiring backpropagation through all updates. The algorithm is versatile and easy to implement. We achieve a new state-of-the art for model-free agents on the Atari ALE benchmark, improve upon MAML in few-shot learning, and demonstrate how our approach opens up new possibilities by meta-learning efficient exploration in a Q-learning agent.
The Option Keyboard: Combining Skills in Reinforcement Learning
Jun 24, 2021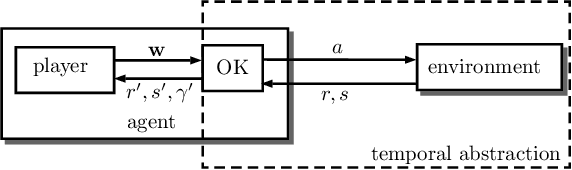
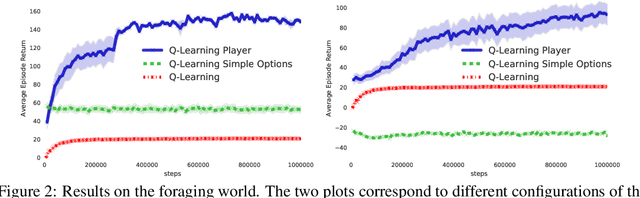
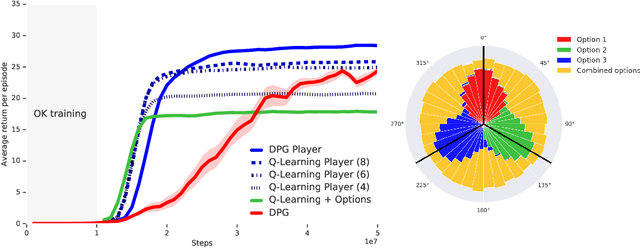
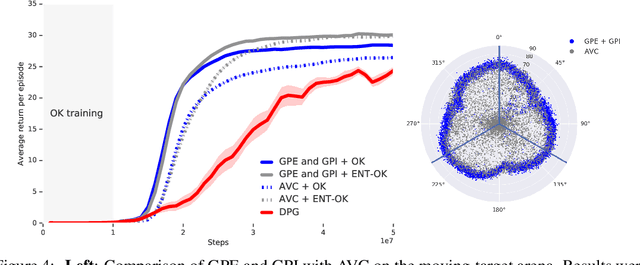
Abstract:The ability to combine known skills to create new ones may be crucial in the solution of complex reinforcement learning problems that unfold over extended periods. We argue that a robust way of combining skills is to define and manipulate them in the space of pseudo-rewards (or "cumulants"). Based on this premise, we propose a framework for combining skills using the formalism of options. We show that every deterministic option can be unambiguously represented as a cumulant defined in an extended domain. Building on this insight and on previous results on transfer learning, we show how to approximate options whose cumulants are linear combinations of the cumulants of known options. This means that, once we have learned options associated with a set of cumulants, we can instantaneously synthesise options induced by any linear combination of them, without any learning involved. We describe how this framework provides a hierarchical interface to the environment whose abstract actions correspond to combinations of basic skills. We demonstrate the practical benefits of our approach in a resource management problem and a navigation task involving a quadrupedal simulated robot.
Proper Value Equivalence
Jun 18, 2021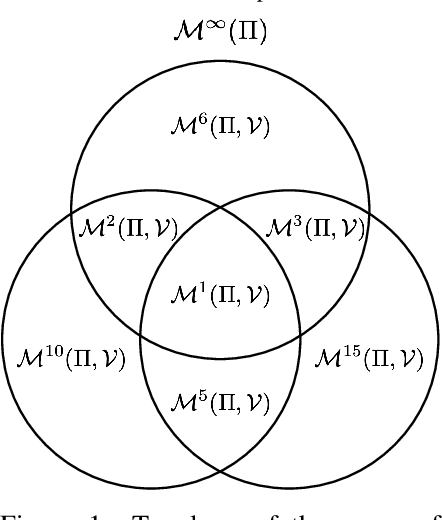

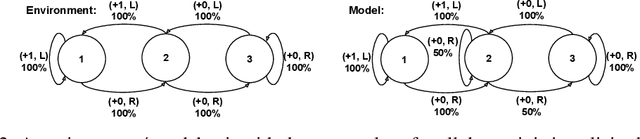
Abstract:One of the main challenges in model-based reinforcement learning (RL) is to decide which aspects of the environment should be modeled. The value-equivalence (VE) principle proposes a simple answer to this question: a model should capture the aspects of the environment that are relevant for value-based planning. Technically, VE distinguishes models based on a set of policies and a set of functions: a model is said to be VE to the environment if the Bellman operators it induces for the policies yield the correct result when applied to the functions. As the number of policies and functions increase, the set of VE models shrinks, eventually collapsing to a single point corresponding to a perfect model. A fundamental question underlying the VE principle is thus how to select the smallest sets of policies and functions that are sufficient for planning. In this paper we take an important step towards answering this question. We start by generalizing the concept of VE to order-$k$ counterparts defined with respect to $k$ applications of the Bellman operator. This leads to a family of VE classes that increase in size as $k \rightarrow \infty$. In the limit, all functions become value functions, and we have a special instantiation of VE which we call proper VE or simply PVE. Unlike VE, the PVE class may contain multiple models even in the limit when all value functions are used. Crucially, all these models are sufficient for planning, meaning that they will yield an optimal policy despite the fact that they may ignore many aspects of the environment. We construct a loss function for learning PVE models and argue that popular algorithms such as MuZero and Muesli can be understood as minimizing an upper bound for this loss. We leverage this connection to propose a modification to MuZero and show that it can lead to improved performance in practice.
Learning and Planning in Complex Action Spaces
Apr 13, 2021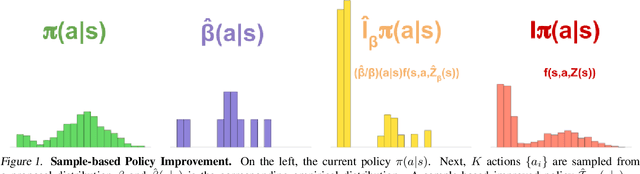
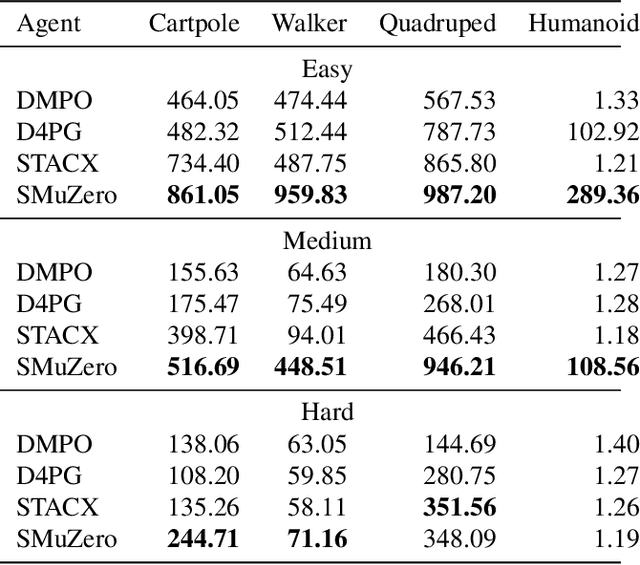
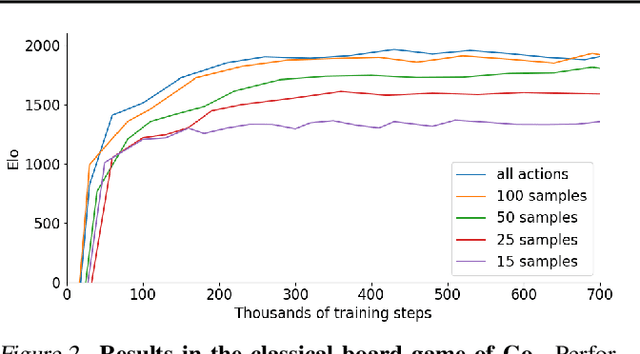
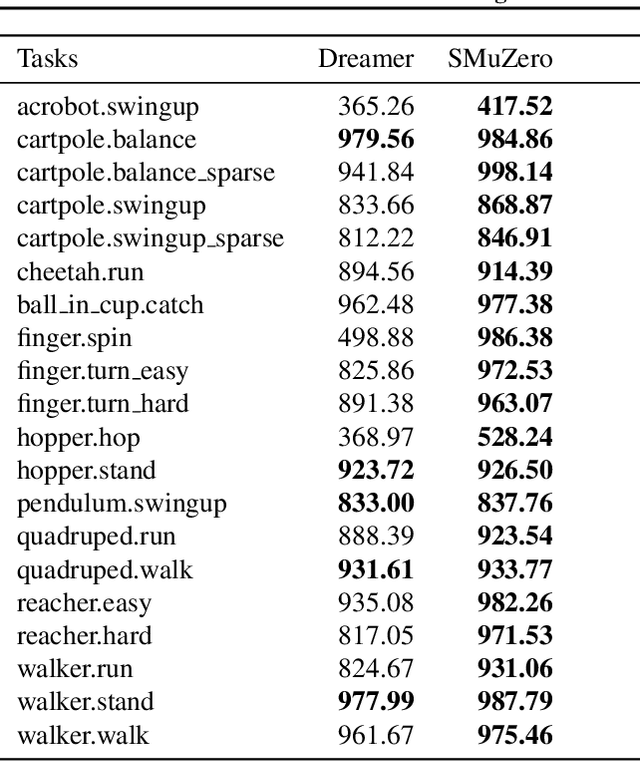
Abstract:Many important real-world problems have action spaces that are high-dimensional, continuous or both, making full enumeration of all possible actions infeasible. Instead, only small subsets of actions can be sampled for the purpose of policy evaluation and improvement. In this paper, we propose a general framework to reason in a principled way about policy evaluation and improvement over such sampled action subsets. This sample-based policy iteration framework can in principle be applied to any reinforcement learning algorithm based upon policy iteration. Concretely, we propose Sampled MuZero, an extension of the MuZero algorithm that is able to learn in domains with arbitrarily complex action spaces by planning over sampled actions. We demonstrate this approach on the classical board game of Go and on two continuous control benchmark domains: DeepMind Control Suite and Real-World RL Suite.
Online and Offline Reinforcement Learning by Planning with a Learned Model
Apr 13, 2021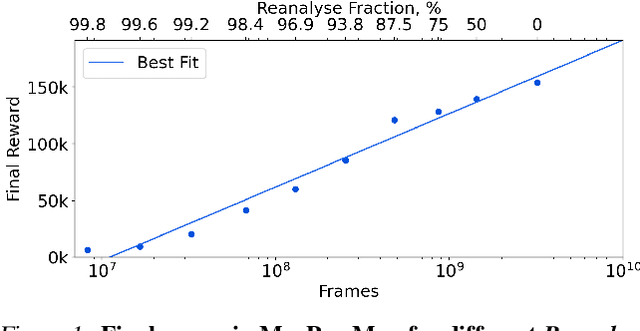
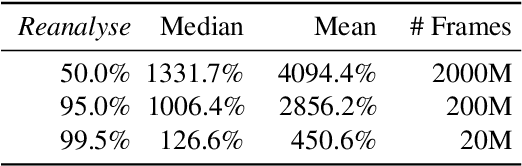
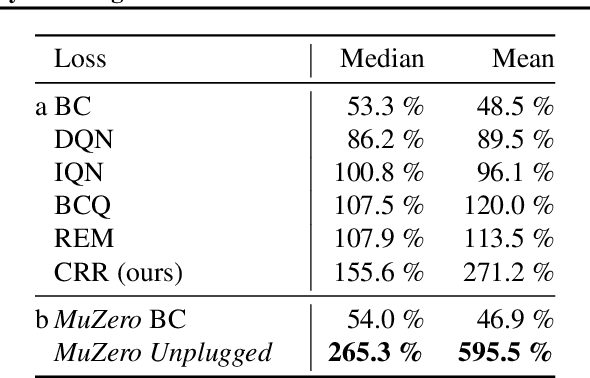
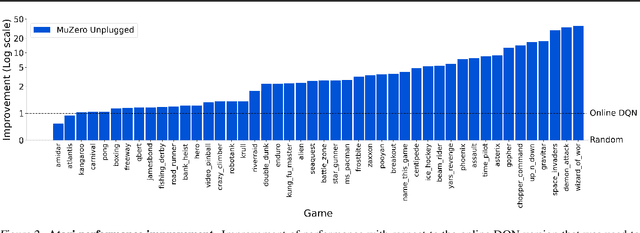
Abstract:Learning efficiently from small amounts of data has long been the focus of model-based reinforcement learning, both for the online case when interacting with the environment and the offline case when learning from a fixed dataset. However, to date no single unified algorithm could demonstrate state-of-the-art results in both settings. In this work, we describe the Reanalyse algorithm which uses model-based policy and value improvement operators to compute new improved training targets on existing data points, allowing efficient learning for data budgets varying by several orders of magnitude. We further show that Reanalyse can also be used to learn entirely from demonstrations without any environment interactions, as in the case of offline Reinforcement Learning (offline RL). Combining Reanalyse with the MuZero algorithm, we introduce MuZero Unplugged, a single unified algorithm for any data budget, including offline RL. In contrast to previous work, our algorithm does not require any special adaptations for the off-policy or offline RL settings. MuZero Unplugged sets new state-of-the-art results in the RL Unplugged offline RL benchmark as well as in the online RL benchmark of Atari in the standard 200 million frame setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge