Generative Hierarchical Materials Search

Generative models trained at scale can now produce text, video, and more recently, scientific data such as crystal structures. In applications of generative approaches to materials science, and in particular to crystal structures, the guidance from the domain expert in the form of high-level instructions can be essential for an automated system to output candidate crystals that are viable for downstream research. In this work, we formulate end-to-end language-to-structure generation as a multi-objective optimization problem, and propose Generative Hierarchical Materials Search (GenMS) for controllable generation of crystal structures. GenMS consists of (1) a language model that takes high-level natural language as input and generates intermediate textual information about a crystal (e.g., chemical formulae), and (2) a diffusion model that takes intermediate information as input and generates low-level continuous value crystal structures. GenMS additionally uses a graph neural network to predict properties (e.g., formation energy) from the generated crystal structures. During inference, GenMS leverages all three components to conduct a forward tree search over the space of possible structures. Experiments show that GenMS outperforms other alternatives of directly using language models to generate structures both in satisfying user request and in generating low-energy structures. We confirm that GenMS is able to generate common crystal structures such as double perovskites, or spinels, solely from natural language input, and hence can form the foundation for more complex structure generation in near future.

Applications of flow models to the generation of correlated lattice QCD ensembles

Machine-learned normalizing flows can be used in the context of lattice quantum field theory to generate statistically correlated ensembles of lattice gauge fields at different action parameters. This work demonstrates how these correlations can be exploited for variance reduction in the computation of observables. Three different proof-of-concept applications are demonstrated using a novel residual flow architecture: continuum limits of gauge theories, the mass dependence of QCD observables, and hadronic matrix elements based on the Feynman-Hellmann approach. In all three cases, it is shown that statistical uncertainties are significantly reduced when machine-learned flows are incorporated as compared with the same calculations performed with uncorrelated ensembles or direct reweighting.

Combining Behaviors with the Successor Features Keyboard

The Option Keyboard (OK) was recently proposed as a method for transferring behavioral knowledge across tasks. OK transfers knowledge by adaptively combining subsets of known behaviors using Successor Features (SFs) and Generalized Policy Improvement (GPI). However, it relies on hand-designed state-features and task encodings which are cumbersome to design for every new environment. In this work, we propose the "Successor Features Keyboard" (SFK), which enables transfer with discovered state-features and task encodings. To enable discovery, we propose the "Categorical Successor Feature Approximator" (CSFA), a novel learning algorithm for estimating SFs while jointly discovering state-features and task encodings. With SFK and CSFA, we achieve the first demonstration of transfer with SFs in a challenging 3D environment where all the necessary representations are discovered. We first compare CSFA against other methods for approximating SFs and show that only CSFA discovers representations compatible with SF&GPI at this scale. We then compare SFK against transfer learning baselines and show that it transfers most quickly to long-horizon tasks.

Advances in machine-learning-based sampling motivated by lattice quantum chromodynamics

Sampling from known probability distributions is a ubiquitous task in computational science, underlying calculations in domains from linguistics to biology and physics. Generative machine-learning (ML) models have emerged as a promising tool in this space, building on the success of this approach in applications such as image, text, and audio generation. Often, however, generative tasks in scientific domains have unique structures and features -- such as complex symmetries and the requirement of exactness guarantees -- that present both challenges and opportunities for ML. This Perspective outlines the advances in ML-based sampling motivated by lattice quantum field theory, in particular for the theory of quantum chromodynamics. Enabling calculations of the structure and interactions of matter from our most fundamental understanding of particle physics, lattice quantum chromodynamics is one of the main consumers of open-science supercomputing worldwide. The design of ML algorithms for this application faces profound challenges, including the necessity of scaling custom ML architectures to the largest supercomputers, but also promises immense benefits, and is spurring a wave of development in ML-based sampling more broadly. In lattice field theory, if this approach can realize its early promise it will be a transformative step towards first-principles physics calculations in particle, nuclear and condensed matter physics that are intractable with traditional approaches.

Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Laser: Latent Set Representations for 3D Generative Modeling

NeRF provides unparalleled fidelity of novel view synthesis: rendering a 3D scene from an arbitrary viewpoint. NeRF requires training on a large number of views that fully cover a scene, which limits its applicability. While these issues can be addressed by learning a prior over scenes in various forms, previous approaches have been either applied to overly simple scenes or struggling to render unobserved parts. We introduce Laser-NV: a generative model which achieves high modelling capacity, and which is based on a set-valued latent representation modelled by normalizing flows. Similarly to previous amortized approaches, Laser-NV learns structure from multiple scenes and is capable of fast, feed-forward inference from few views. To encourage higher rendering fidelity and consistency with observed views, Laser-NV further incorporates a geometry-informed attention mechanism over the observed views. Laser-NV further produces diverse and plausible completions of occluded parts of a scene while remaining consistent with observations. Laser-NV shows state-of-the-art novel-view synthesis quality when evaluated on ShapeNet and on a novel simulated City dataset, which features high uncertainty in the unobserved regions of the scene.

Aspects of scaling and scalability for flow-based sampling of lattice QCD

Recent applications of machine-learned normalizing flows to sampling in lattice field theory suggest that such methods may be able to mitigate critical slowing down and topological freezing. However, these demonstrations have been at the scale of toy models, and it remains to be determined whether they can be applied to state-of-the-art lattice quantum chromodynamics calculations. Assessing the viability of sampling algorithms for lattice field theory at scale has traditionally been accomplished using simple cost scaling laws, but as we discuss in this work, their utility is limited for flow-based approaches. We conclude that flow-based approaches to sampling are better thought of as a broad family of algorithms with different scaling properties, and that scalability must be assessed experimentally.

Gauge-equivariant flow models for sampling in lattice field theories with pseudofermions

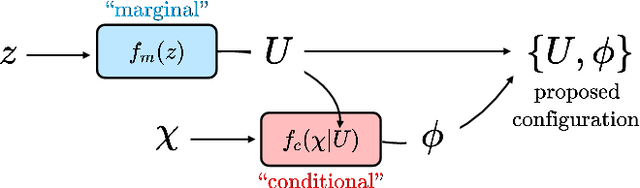
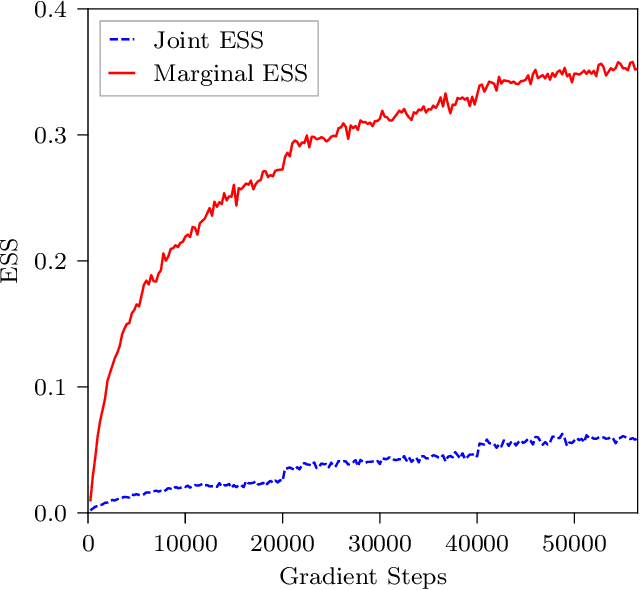
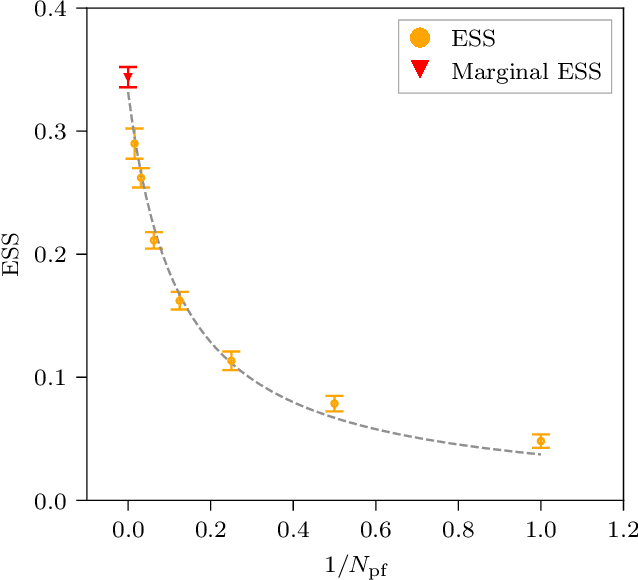
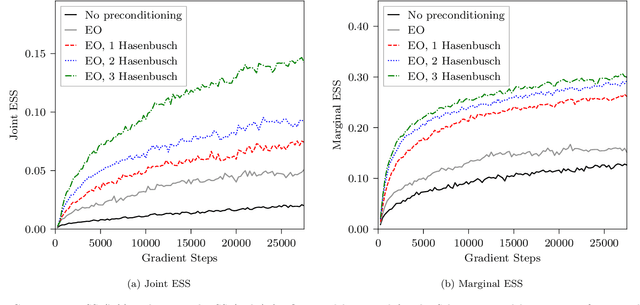
This work presents gauge-equivariant architectures for flow-based sampling in fermionic lattice field theories using pseudofermions as stochastic estimators for the fermionic determinant. This is the default approach in state-of-the-art lattice field theory calculations, making this development critical to the practical application of flow models to theories such as QCD. Methods by which flow-based sampling approaches can be improved via standard techniques such as even/odd preconditioning and the Hasenbusch factorization are also outlined. Numerical demonstrations in two-dimensional U(1) and SU(3) gauge theories with $N_f=2$ flavors of fermions are provided.

Flow-based sampling in the lattice Schwinger model at criticality

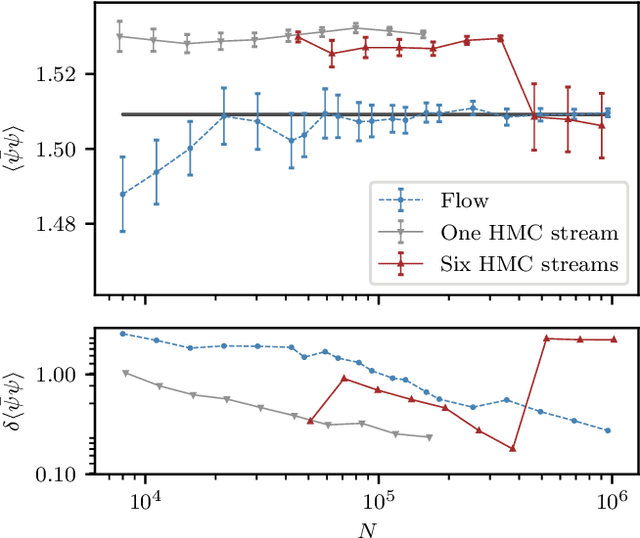
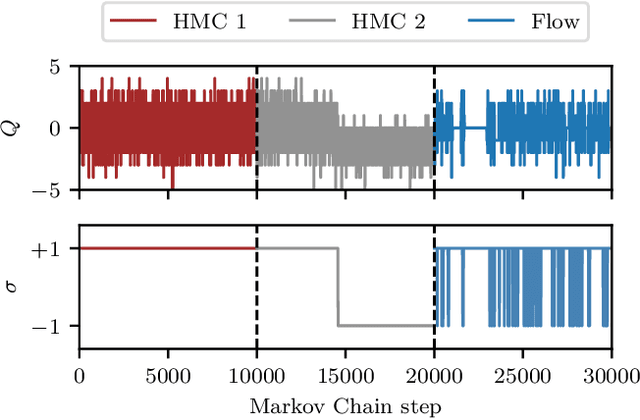
Recent results suggest that flow-based algorithms may provide efficient sampling of field distributions for lattice field theory applications, such as studies of quantum chromodynamics and the Schwinger model. In this work, we provide a numerical demonstration of robust flow-based sampling in the Schwinger model at the critical value of the fermion mass. In contrast, at the same parameters, conventional methods fail to sample all parts of configuration space, leading to severely underestimated uncertainties.

Continual Repeated Annealed Flow Transport Monte Carlo

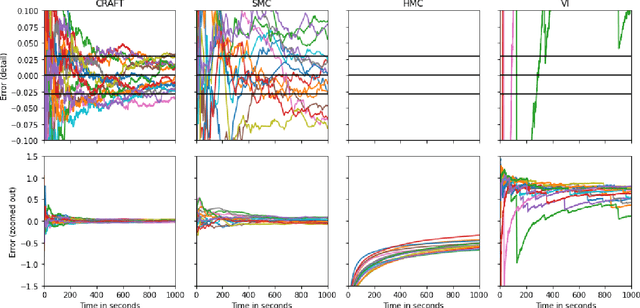
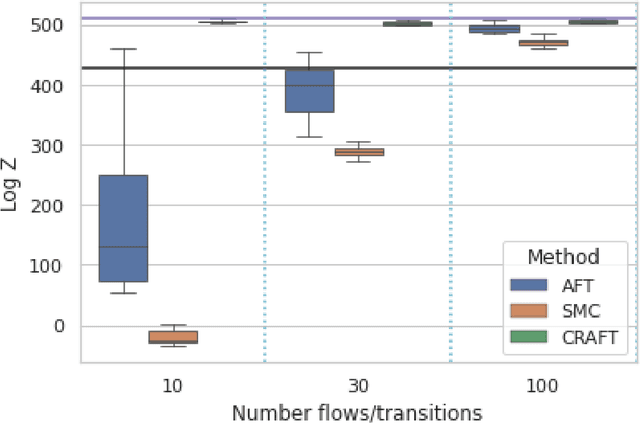
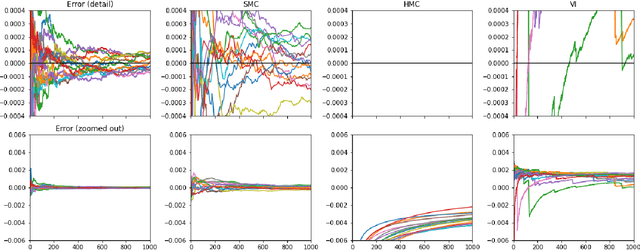
We propose Continual Repeated Annealed Flow Transport Monte Carlo (CRAFT), a method that combines a sequential Monte Carlo (SMC) sampler (itself a generalization of Annealed Importance Sampling) with variational inference using normalizing flows. The normalizing flows are directly trained to transport between annealing temperatures using a KL divergence for each transition. This optimization objective is itself estimated using the normalizing flow/SMC approximation. We show conceptually and using multiple empirical examples that CRAFT improves on Annealed Flow Transport Monte Carlo (Arbel et al., 2021), on which it builds and also on Markov chain Monte Carlo (MCMC) based Stochastic Normalizing Flows (Wu et al., 2020). By incorporating CRAFT within particle MCMC, we show that such learnt samplers can achieve impressively accurate results on a challenging lattice field theory example.