Statistical-Computational Trade-offs for Density Estimation

We study the density estimation problem defined as follows: given $k$ distributions $p_1, \ldots, p_k$ over a discrete domain $[n]$, as well as a collection of samples chosen from a ``query'' distribution $q$ over $[n]$, output $p_i$ that is ``close'' to $q$. Recently~\cite{aamand2023data} gave the first and only known result that achieves sublinear bounds in {\em both} the sampling complexity and the query time while preserving polynomial data structure space. However, their improvement over linear samples and time is only by subpolynomial factors. Our main result is a lower bound showing that, for a broad class of data structures, their bounds cannot be significantly improved. In particular, if an algorithm uses $O(n/\log^c k)$ samples for some constant $c>0$ and polynomial space, then the query time of the data structure must be at least $k^{1-O(1)/\log \log k}$, i.e., close to linear in the number of distributions $k$. This is a novel \emph{statistical-computational} trade-off for density estimation, demonstrating that any data structure must use close to a linear number of samples or take close to linear query time. The lower bound holds even in the realizable case where $q=p_i$ for some $i$, and when the distributions are flat (specifically, all distributions are uniform over half of the domain $[n]$). We also give a simple data structure for our lower bound instance with asymptotically matching upper bounds. Experiments show that the data structure is quite efficient in practice.

SparseCL: Sparse Contrastive Learning for Contradiction Retrieval

Contradiction retrieval refers to identifying and extracting documents that explicitly disagree with or refute the content of a query, which is important to many downstream applications like fact checking and data cleaning. To retrieve contradiction argument to the query from large document corpora, existing methods such as similarity search and crossencoder models exhibit significant limitations. The former struggles to capture the essence of contradiction due to its inherent nature of favoring similarity, while the latter suffers from computational inefficiency, especially when the size of corpora is large. To address these challenges, we introduce a novel approach: SparseCL that leverages specially trained sentence embeddings designed to preserve subtle, contradictory nuances between sentences. Our method utilizes a combined metric of cosine similarity and a sparsity function to efficiently identify and retrieve documents that contradict a given query. This approach dramatically enhances the speed of contradiction detection by reducing the need for exhaustive document comparisons to simple vector calculations. We validate our model using the Arguana dataset, a benchmark dataset specifically geared towards contradiction retrieval, as well as synthetic contradictions generated from the MSMARCO and HotpotQA datasets using GPT-4. Our experiments demonstrate the efficacy of our approach not only in contradiction retrieval with more than 30% accuracy improvements on MSMARCO and HotpotQA across different model architectures but also in applications such as cleaning corrupted corpora to restore high-quality QA retrieval. This paper outlines a promising direction for improving the accuracy and efficiency of contradiction retrieval in large-scale text corpora.

A Bi-metric Framework for Fast Similarity Search

We propose a new "bi-metric" framework for designing nearest neighbor data structures. Our framework assumes two dissimilarity functions: a ground-truth metric that is accurate but expensive to compute, and a proxy metric that is cheaper but less accurate. In both theory and practice, we show how to construct data structures using only the proxy metric such that the query procedure achieves the accuracy of the expensive metric, while only using a limited number of calls to both metrics. Our theoretical results instantiate this framework for two popular nearest neighbor search algorithms: DiskANN and Cover Tree. In both cases we show that, as long as the proxy metric used to construct the data structure approximates the ground-truth metric up to a bounded factor, our data structure achieves arbitrarily good approximation guarantees with respect to the ground-truth metric. On the empirical side, we apply the framework to the text retrieval problem with two dissimilarity functions evaluated by ML models with vastly different computational costs. We observe that for almost all data sets in the MTEB benchmark, our approach achieves a considerably better accuracy-efficiency tradeoff than the alternatives, such as re-ranking.

Worst-case Performance of Popular Approximate Nearest Neighbor Search Implementations: Guarantees and Limitations

Graph-based approaches to nearest neighbor search are popular and powerful tools for handling large datasets in practice, but they have limited theoretical guarantees. We study the worst-case performance of recent graph-based approximate nearest neighbor search algorithms, such as HNSW, NSG and DiskANN. For DiskANN, we show that its "slow preprocessing" version provably supports approximate nearest neighbor search query with constant approximation ratio and poly-logarithmic query time, on data sets with bounded "intrinsic" dimension. For the other data structure variants studied, including DiskANN with "fast preprocessing", HNSW and NSG, we present a family of instances on which the empirical query time required to achieve a "reasonable" accuracy is linear in instance size. For example, for DiskANN, we show that the query procedure can take at least $0.1 n$ steps on instances of size $n$ before it encounters any of the $5$ nearest neighbors of the query.

A Universal Discriminator for Zero-Shot Generalization

Generative modeling has been the dominant approach for large-scale pretraining and zero-shot generalization. In this work, we challenge this convention by showing that discriminative approaches perform substantially better than generative ones on a large number of NLP tasks. Technically, we train a single discriminator to predict whether a text sample comes from the true data distribution, similar to GANs. Since many NLP tasks can be formulated as selecting from a few options, we use this discriminator to predict the option with the highest probability. This simple formulation achieves state-of-the-art zero-shot results on the T0 benchmark, outperforming T0 by 16.0\%, 7.8\%, and 11.5\% respectively on different scales. In the finetuning setting, our approach also achieves new state-of-the-art results on a wide range of NLP tasks, with only 1/4 parameters of previous methods. Meanwhile, our approach requires minimal prompting efforts, which largely improves robustness and is essential for real-world applications. Furthermore, we also jointly train a generalized UD in combination with generative tasks, which maintains its advantage on discriminative tasks and simultaneously works on generative tasks.

Embeddings and labeling schemes for A*

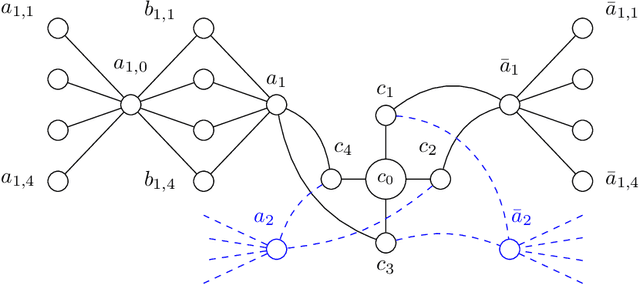
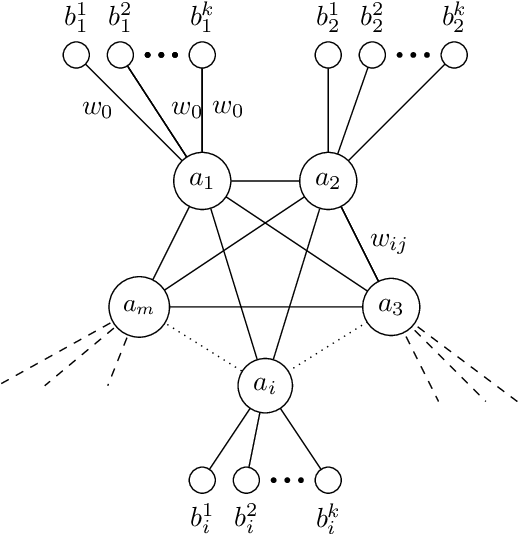
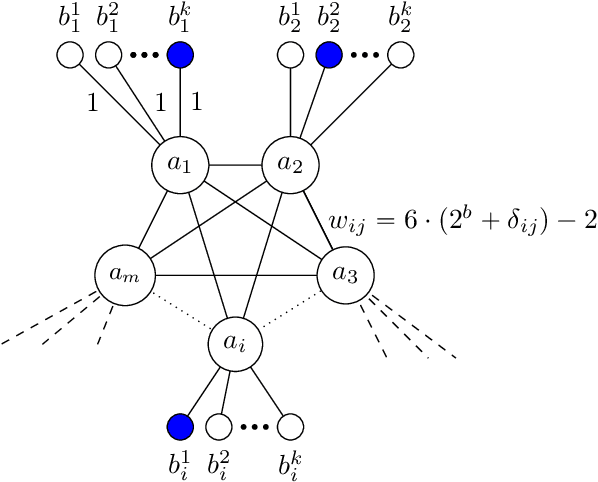
A* is a classic and popular method for graphs search and path finding. It assumes the existence of a heuristic function $h(u,t)$ that estimates the shortest distance from any input node $u$ to the destination $t$. Traditionally, heuristics have been handcrafted by domain experts. However, over the last few years, there has been a growing interest in learning heuristic functions. Such learned heuristics estimate the distance between given nodes based on "features" of those nodes. In this paper we formalize and initiate the study of such feature-based heuristics. In particular, we consider heuristics induced by norm embeddings and distance labeling schemes, and provide lower bounds for the tradeoffs between the number of dimensions or bits used to represent each graph node, and the running time of the A* algorithm. We also show that, under natural assumptions, our lower bounds are almost optimal.

Simple Combinatorial Algorithms for Combinatorial Bandits: Corruptions and Approximations

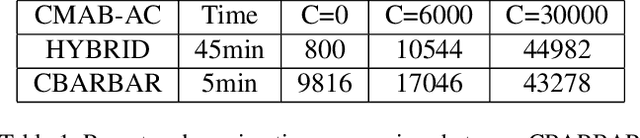
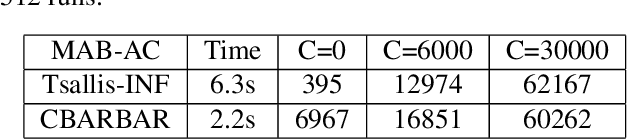
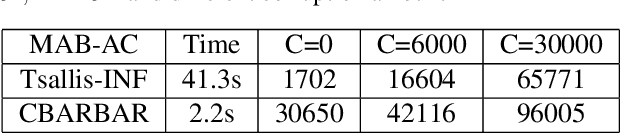
We consider the stochastic combinatorial semi-bandit problem with adversarial corruptions. We provide a simple combinatorial algorithm that can achieve a regret of $\tilde{O}\left(C+d^2K/\Delta_{min}\right)$ where $C$ is the total amount of corruptions, $d$ is the maximal number of arms one can play in each round, $K$ is the number of arms. If one selects only one arm in each round, we achieves a regret of $\tilde{O}\left(C+\sum_{\Delta_i>0}(1/\Delta_i)\right)$. Our algorithm is combinatorial and improves on the previous combinatorial algorithm by [Gupta et al., COLT2019] (their bound is $\tilde{O}\left(KC+\sum_{\Delta_i>0}(1/\Delta_i)\right)$), and almost matches the best known bounds obtained by [Zimmert et al., ICML2019] and [Zimmert and Seldin, AISTATS2019] (up to logarithmic factor). Note that the algorithms in [Zimmert et al., ICML2019] and [Zimmert and Seldin, AISTATS2019] require one to solve complex convex programs while our algorithm is combinatorial, very easy to implement, requires weaker assumptions and has very low oracle complexity and running time. We also study the setting where we only get access to an approximation oracle for the stochastic combinatorial semi-bandit problem. Our algorithm achieves an (approximation) regret bound of $\tilde{O}\left(d\sqrt{KT}\right)$. Our algorithm is very simple, only worse than the best known regret bound by $\sqrt{d}$, and has much lower oracle complexity than previous work.

Fine-Grained Gap-Dependent Bounds for Tabular MDPs via Adaptive Multi-Step Bootstrap

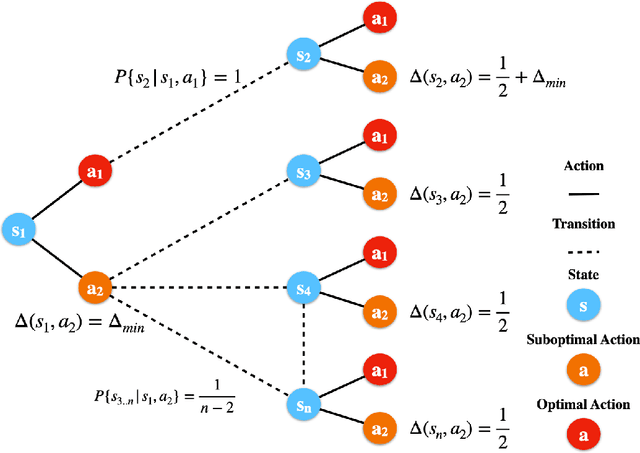
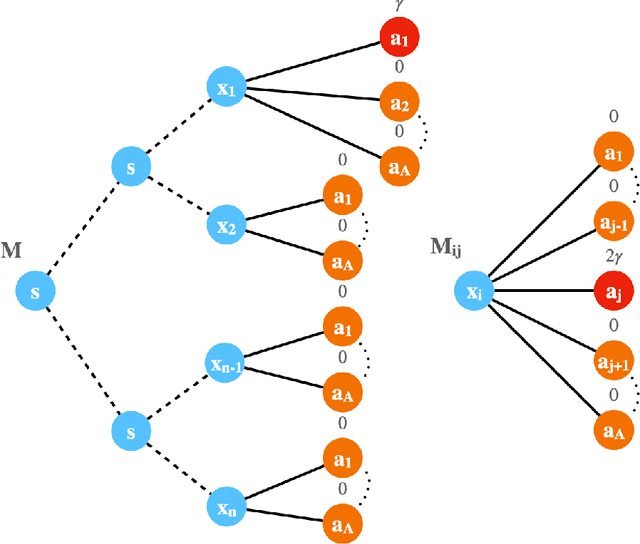
This paper presents a new model-free algorithm for episodic finite-horizon Markov Decision Processes (MDP), Adaptive Multi-step Bootstrap (AMB), which enjoys a stronger gap-dependent regret bound. The first innovation is to estimate the optimal $Q$-function by combining an optimistic bootstrap with an adaptive multi-step Monte Carlo rollout. The second innovation is to select the action with the largest confidence interval length among admissible actions that are not dominated by any other actions. We show when each state has a unique optimal action, AMB achieves a gap-dependent regret bound that only scales with the sum of the inverse of the sub-optimality gaps. In contrast, Simchowitz and Jamieson (2019) showed all upper-confidence-bound (UCB) algorithms suffer an additional $\Omega\left(\frac{S}{\Delta_{min}}\right)$ regret due to over-exploration where $\Delta_{min}$ is the minimum sub-optimality gap and $S$ is the number of states. We further show that for general MDPs, AMB suffers an additional $\frac{|Z_{mul}|}{\Delta_{min}}$ regret, where $Z_{mul}$ is the set of state-action pairs $(s,a)$'s satisfying $a$ is a non-unique optimal action for $s$. We complement our upper bound with a lower bound showing the dependency on $\frac{|Z_{mul}|}{\Delta_{min}}$ is unavoidable for any consistent algorithm. This lower bound also implies a separation between reinforcement learning and contextual bandits.