Talya Eden
Triangle and Four Cycle Counting with Predictions in Graph Streams
Mar 17, 2022
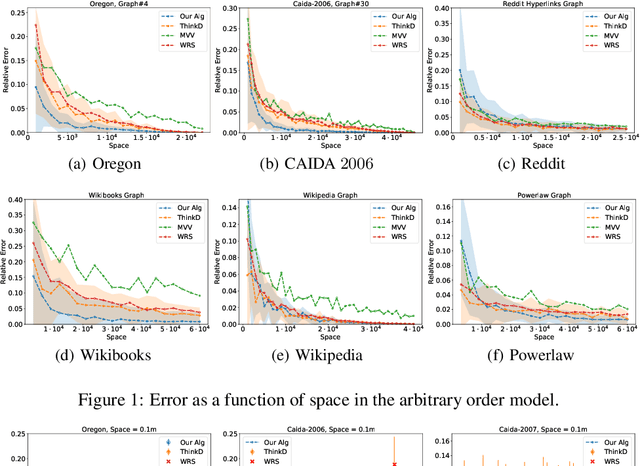
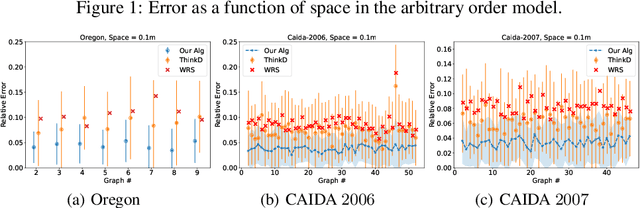
Abstract:We propose data-driven one-pass streaming algorithms for estimating the number of triangles and four cycles, two fundamental problems in graph analytics that are widely studied in the graph data stream literature. Recently, (Hsu 2018) and (Jiang 2020) applied machine learning techniques in other data stream problems, using a trained oracle that can predict certain properties of the stream elements to improve on prior "classical" algorithms that did not use oracles. In this paper, we explore the power of a "heavy edge" oracle in multiple graph edge streaming models. In the adjacency list model, we present a one-pass triangle counting algorithm improving upon the previous space upper bounds without such an oracle. In the arbitrary order model, we present algorithms for both triangle and four cycle estimation with fewer passes and the same space complexity as in previous algorithms, and we show several of these bounds are optimal. We analyze our algorithms under several noise models, showing that the algorithms perform well even when the oracle errs. Our methodology expands upon prior work on "classical" streaming algorithms, as previous multi-pass and random order streaming algorithms can be seen as special cases of our algorithms, where the first pass or random order was used to implement the heavy edge oracle. Lastly, our experiments demonstrate advantages of the proposed method compared to state-of-the-art streaming algorithms.
Embeddings and labeling schemes for A*
Nov 19, 2021
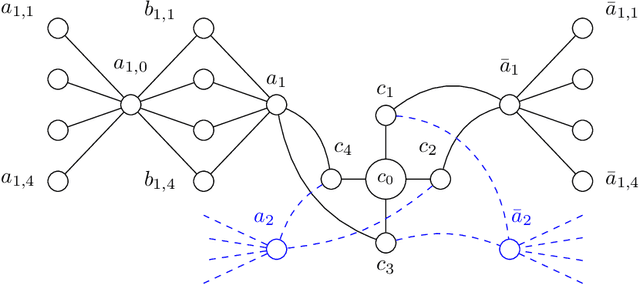
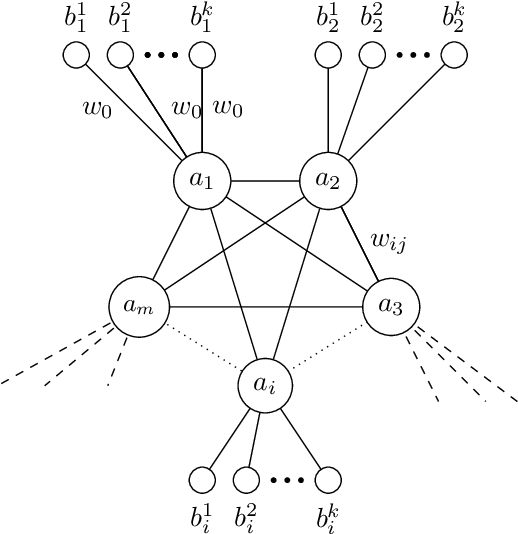
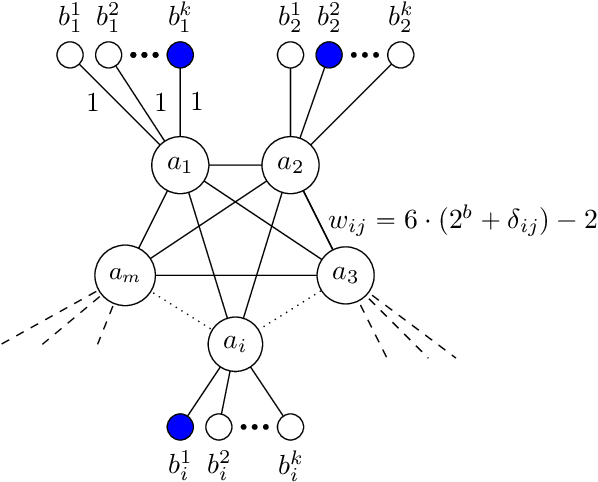
Abstract:A* is a classic and popular method for graphs search and path finding. It assumes the existence of a heuristic function $h(u,t)$ that estimates the shortest distance from any input node $u$ to the destination $t$. Traditionally, heuristics have been handcrafted by domain experts. However, over the last few years, there has been a growing interest in learning heuristic functions. Such learned heuristics estimate the distance between given nodes based on "features" of those nodes. In this paper we formalize and initiate the study of such feature-based heuristics. In particular, we consider heuristics induced by norm embeddings and distance labeling schemes, and provide lower bounds for the tradeoffs between the number of dimensions or bits used to represent each graph node, and the running time of the A* algorithm. We also show that, under natural assumptions, our lower bounds are almost optimal.
Learning-based Support Estimation in Sublinear Time
Jun 15, 2021
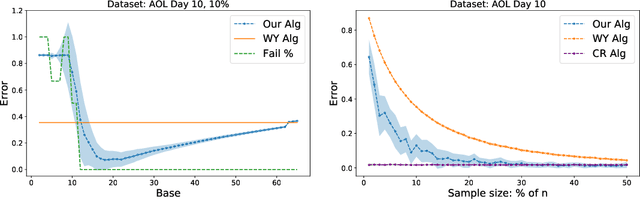
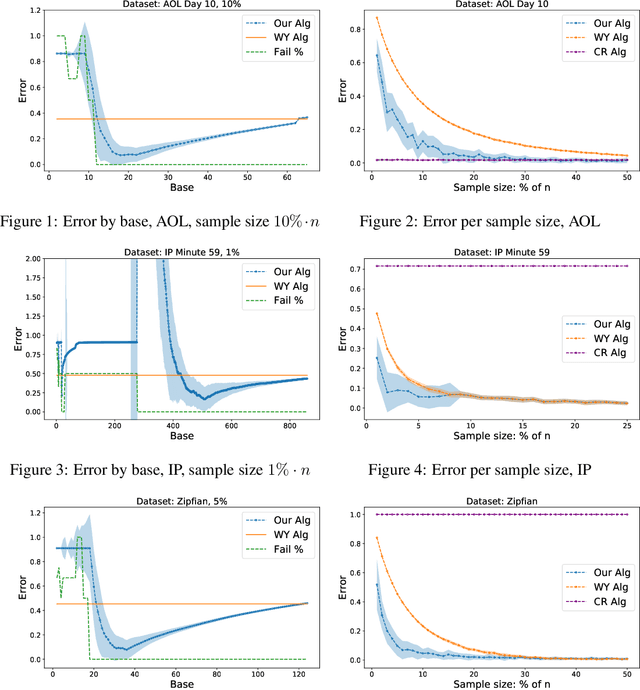
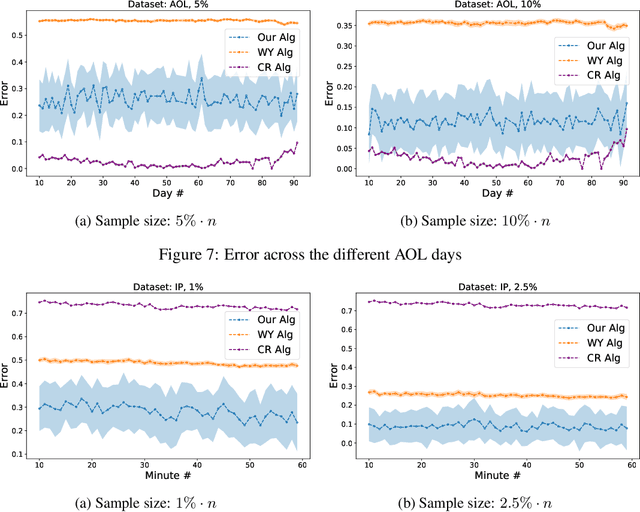
Abstract:We consider the problem of estimating the number of distinct elements in a large data set (or, equivalently, the support size of the distribution induced by the data set) from a random sample of its elements. The problem occurs in many applications, including biology, genomics, computer systems and linguistics. A line of research spanning the last decade resulted in algorithms that estimate the support up to $ \pm \varepsilon n$ from a sample of size $O(\log^2(1/\varepsilon) \cdot n/\log n)$, where $n$ is the data set size. Unfortunately, this bound is known to be tight, limiting further improvements to the complexity of this problem. In this paper we consider estimation algorithms augmented with a machine-learning-based predictor that, given any element, returns an estimation of its frequency. We show that if the predictor is correct up to a constant approximation factor, then the sample complexity can be reduced significantly, to \[ \ \log (1/\varepsilon) \cdot n^{1-\Theta(1/\log(1/\varepsilon))}. \] We evaluate the proposed algorithms on a collection of data sets, using the neural-network based estimators from {Hsu et al, ICLR'19} as predictors. Our experiments demonstrate substantial (up to 3x) improvements in the estimation accuracy compared to the state of the art algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge