PerceptionLM: Open-Access Data and Models for Detailed Visual Understanding

Vision-language models are integral to computer vision research, yet many high-performing models remain closed-source, obscuring their data, design and training recipe. The research community has responded by using distillation from black-box models to label training data, achieving strong benchmark results, at the cost of measurable scientific progress. However, without knowing the details of the teacher model and its data sources, scientific progress remains difficult to measure. In this paper, we study building a Perception Language Model (PLM) in a fully open and reproducible framework for transparent research in image and video understanding. We analyze standard training pipelines without distillation from proprietary models and explore large-scale synthetic data to identify critical data gaps, particularly in detailed video understanding. To bridge these gaps, we release 2.8M human-labeled instances of fine-grained video question-answer pairs and spatio-temporally grounded video captions. Additionally, we introduce PLM-VideoBench, a suite for evaluating challenging video understanding tasks focusing on the ability to reason about "what", "where", "when", and "how" of a video. We make our work fully reproducible by providing data, training recipes, code & models.

Perception Encoder: The best visual embeddings are not at the output of the network

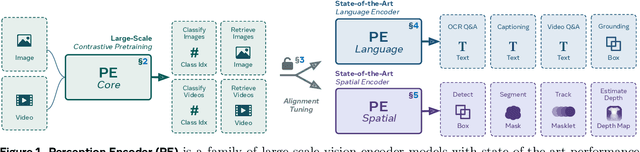
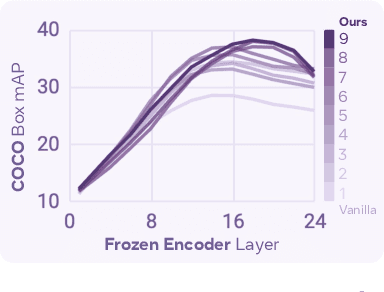
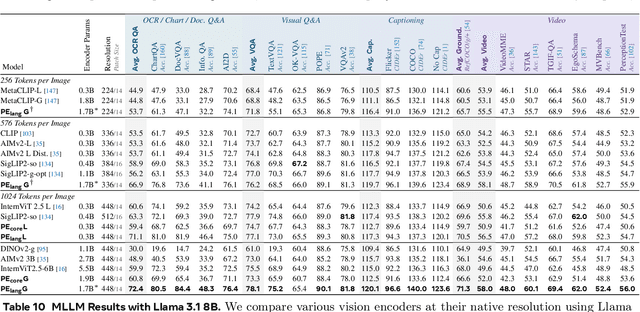
We introduce Perception Encoder (PE), a state-of-the-art encoder for image and video understanding trained via simple vision-language learning. Traditionally, vision encoders have relied on a variety of pretraining objectives, each tailored to specific downstream tasks such as classification, captioning, or localization. Surprisingly, after scaling our carefully tuned image pretraining recipe and refining with our robust video data engine, we find that contrastive vision-language training alone can produce strong, general embeddings for all of these downstream tasks. There is only one caveat: these embeddings are hidden within the intermediate layers of the network. To draw them out, we introduce two alignment methods, language alignment for multimodal language modeling, and spatial alignment for dense prediction. Together with the core contrastive checkpoint, our PE family of models achieves state-of-the-art performance on a wide variety of tasks, including zero-shot image and video classification and retrieval; document, image, and video Q&A; and spatial tasks such as detection, depth estimation, and tracking. To foster further research, we are releasing our models, code, and a novel dataset of synthetically and human-annotated videos.

Formal Theorem Proving by Rewarding LLMs to Decompose Proofs Hierarchically

Mathematical theorem proving is an important testbed for large language models' deep and abstract reasoning capability. This paper focuses on improving LLMs' ability to write proofs in formal languages that permit automated proof verification/evaluation. Most previous results provide human-written lemmas to the theorem prover, which is an arguably oversimplified setting that does not sufficiently test the provers' planning and decomposition capabilities. Instead, we work in a more natural setup where the lemmas that are directly relevant to the theorem are not given to the theorem prover at test time. We design an RL-based training algorithm that encourages the model to decompose a theorem into lemmas, prove the lemmas, and then prove the theorem by using the lemmas. Our reward mechanism is inspired by how mathematicians train themselves: even if a theorem is too challenging to be proved by the current model, a positive reward is still given to the model for any correct and novel lemmas that are proposed and proved in this process. During training, our model proposes and proves lemmas that are not in the training dataset. In fact, these newly-proposed correct lemmas consist of 37.7% of the training replay buffer when we train on the dataset extracted from Archive of Formal Proofs (AFP). The model trained by our RL algorithm outperforms that trained by supervised finetuning, improving the pass rate from 40.8% to 45.5% on AFP test set, and from 36.5% to 39.5% on an out-of-distribution test set.

Understanding Warmup-Stable-Decay Learning Rates: A River Valley Loss Landscape Perspective

Training language models currently requires pre-determining a fixed compute budget because the typical cosine learning rate schedule depends on the total number of steps. In contrast, the Warmup-Stable-Decay (WSD) schedule uses a constant learning rate to produce a main branch of iterates that can in principle continue indefinitely without a pre-specified compute budget. Then, given any compute budget, one can branch out from the main branch at a proper at any time with a rapidly decaying learning rate to produce a strong model. Empirically, WSD generates a non-traditional loss curve: the loss remains elevated during the stable phase but sharply declines during the decay phase. Towards explaining this phenomenon, we conjecture that pretraining loss exhibits a river valley landscape, which resembles a deep valley with a river at its bottom. Under this assumption, we show that during the stable phase, the iterate undergoes large oscillations due to the high learning rate, yet it progresses swiftly along the river. During the decay phase, the rapidly dropping learning rate minimizes the iterate's oscillations, moving it closer to the river and revealing true optimization progress. Therefore, the sustained high learning rate phase and fast decaying phase are responsible for progress in the river and the mountain directions respectively, and are both critical. Our analysis predicts phenomenons consistent with empirical observations and shows that this landscape can emerge from pretraining on a simple bi-gram dataset. Inspired by the theory, we introduce WSD-S, a variant of WSD that reuses previous checkpoints' decay phases and keeps only one main branch, where we resume from a decayed checkpoint. WSD-S empirically outperforms WSD and Cyclic-Cosine in obtaining multiple language model checkpoints across various compute budgets in a single run for parameters scaling from 0.1B to 1.2B.

SAM 2: Segment Anything in Images and Videos

We present Segment Anything Model 2 (SAM 2), a foundation model towards solving promptable visual segmentation in images and videos. We build a data engine, which improves model and data via user interaction, to collect the largest video segmentation dataset to date. Our model is a simple transformer architecture with streaming memory for real-time video processing. SAM 2 trained on our data provides strong performance across a wide range of tasks. In video segmentation, we observe better accuracy, using 3x fewer interactions than prior approaches. In image segmentation, our model is more accurate and 6x faster than the Segment Anything Model (SAM). We believe that our data, model, and insights will serve as a significant milestone for video segmentation and related perception tasks. We are releasing a version of our model, the dataset and an interactive demo.

Linguistic Calibration of Language Models

Language models (LMs) may lead their users to make suboptimal downstream decisions when they confidently hallucinate. This issue can be mitigated by having the LM verbally convey the probability that its claims are correct, but existing models cannot produce text with calibrated confidence statements. Through the lens of decision-making, we formalize linguistic calibration for long-form generations: an LM is linguistically calibrated if its generations enable its users to make calibrated probabilistic predictions. This definition enables a training framework where a supervised finetuning step bootstraps an LM to emit long-form generations with confidence statements such as "I estimate a 30% chance of..." or "I am certain that...", followed by a reinforcement learning step which rewards generations that enable a user to provide calibrated answers to related questions. We linguistically calibrate Llama 2 7B and find in automated and human evaluations of long-form generations that it is significantly more calibrated than strong finetuned factuality baselines with comparable accuracy. These findings generalize under distribution shift on question-answering and under a significant task shift to person biography generation. Our results demonstrate that long-form generations may be calibrated end-to-end by constructing an objective in the space of the predictions that users make in downstream decision-making.

Chain of Thought Empowers Transformers to Solve Inherently Serial Problems

Instructing the model to generate a sequence of intermediate steps, a.k.a., a chain of thought (CoT), is a highly effective method to improve the accuracy of large language models (LLMs) on arithmetics and symbolic reasoning tasks. However, the mechanism behind CoT remains unclear. This work provides a theoretical understanding of the power of CoT for decoder-only transformers through the lens of expressiveness. Conceptually, CoT empowers the model with the ability to perform inherently serial computation, which is otherwise lacking in transformers, especially when depth is low. Given input length $n$, previous works have shown that constant-depth transformers with finite precision $\mathsf{poly}(n)$ embedding size can only solve problems in $\mathsf{TC}^0$ without CoT. We first show an even tighter expressiveness upper bound for constant-depth transformers with constant-bit precision, which can only solve problems in $\mathsf{AC}^0$, a proper subset of $ \mathsf{TC}^0$. However, with $T$ steps of CoT, constant-depth transformers using constant-bit precision and $O(\log n)$ embedding size can solve any problem solvable by boolean circuits of size $T$. Empirically, enabling CoT dramatically improves the accuracy for tasks that are hard for parallel computation, including the composition of permutation groups, iterated squaring, and circuit value problems, especially for low-depth transformers.

Trash to Treasure: Low-Light Object Detection via Decomposition-and-Aggregation

Object detection in low-light scenarios has attracted much attention in the past few years. A mainstream and representative scheme introduces enhancers as the pre-processing for regular detectors. However, because of the disparity in task objectives between the enhancer and detector, this paradigm cannot shine at its best ability. In this work, we try to arouse the potential of enhancer + detector. Different from existing works, we extend the illumination-based enhancers (our newly designed or existing) as a scene decomposition module, whose removed illumination is exploited as the auxiliary in the detector for extracting detection-friendly features. A semantic aggregation module is further established for integrating multi-scale scene-related semantic information in the context space. Actually, our built scheme successfully transforms the "trash" (i.e., the ignored illumination in the detector) into the "treasure" for the detector. Plenty of experiments are conducted to reveal our superiority against other state-of-the-art methods. The code will be public if it is accepted.

Sharpness Minimization Algorithms Do Not Only Minimize Sharpness To Achieve Better Generalization

Despite extensive studies, the underlying reason as to why overparameterized neural networks can generalize remains elusive. Existing theory shows that common stochastic optimizers prefer flatter minimizers of the training loss, and thus a natural potential explanation is that flatness implies generalization. This work critically examines this explanation. Through theoretical and empirical investigation, we identify the following three scenarios for two-layer ReLU networks: (1) flatness provably implies generalization; (2) there exist non-generalizing flattest models and sharpness minimization algorithms fail to generalize, and (3) perhaps most surprisingly, there exist non-generalizing flattest models, but sharpness minimization algorithms still generalize. Our results suggest that the relationship between sharpness and generalization subtly depends on the data distributions and the model architectures and sharpness minimization algorithms do not only minimize sharpness to achieve better generalization. This calls for the search for other explanations for the generalization of over-parameterized neural networks.

One Step of Gradient Descent is Provably the Optimal In-Context Learner with One Layer of Linear Self-Attention

Recent works have empirically analyzed in-context learning and shown that transformers trained on synthetic linear regression tasks can learn to implement ridge regression, which is the Bayes-optimal predictor, given sufficient capacity [Aky\"urek et al., 2023], while one-layer transformers with linear self-attention and no MLP layer will learn to implement one step of gradient descent (GD) on a least-squares linear regression objective [von Oswald et al., 2022]. However, the theory behind these observations remains poorly understood. We theoretically study transformers with a single layer of linear self-attention, trained on synthetic noisy linear regression data. First, we mathematically show that when the covariates are drawn from a standard Gaussian distribution, the one-layer transformer which minimizes the pre-training loss will implement a single step of GD on the least-squares linear regression objective. Then, we find that changing the distribution of the covariates and weight vector to a non-isotropic Gaussian distribution has a strong impact on the learned algorithm: the global minimizer of the pre-training loss now implements a single step of $\textit{pre-conditioned}$ GD. However, if only the distribution of the responses is changed, then this does not have a large effect on the learned algorithm: even when the response comes from a more general family of $\textit{nonlinear}$ functions, the global minimizer of the pre-training loss still implements a single step of GD on a least-squares linear regression objective.