$\ell_p$-Regression in the Arbitrary Partition Model of Communication

We consider the randomized communication complexity of the distributed $\ell_p$-regression problem in the coordinator model, for $p\in (0,2]$. In this problem, there is a coordinator and $s$ servers. The $i$-th server receives $A^i\in\{-M, -M+1, \ldots, M\}^{n\times d}$ and $b^i\in\{-M, -M+1, \ldots, M\}^n$ and the coordinator would like to find a $(1+\epsilon)$-approximate solution to $\min_{x\in\mathbb{R}^n} \|(\sum_i A^i)x - (\sum_i b^i)\|_p$. Here $M \leq \mathrm{poly}(nd)$ for convenience. This model, where the data is additively shared across servers, is commonly referred to as the arbitrary partition model. We obtain significantly improved bounds for this problem. For $p = 2$, i.e., least squares regression, we give the first optimal bound of $\tilde{\Theta}(sd^2 + sd/\epsilon)$ bits. For $p \in (1,2)$,we obtain an $\tilde{O}(sd^2/\epsilon + sd/\mathrm{poly}(\epsilon))$ upper bound. Notably, for $d$ sufficiently large, our leading order term only depends linearly on $1/\epsilon$ rather than quadratically. We also show communication lower bounds of $\Omega(sd^2 + sd/\epsilon^2)$ for $p\in (0,1]$ and $\Omega(sd^2 + sd/\epsilon)$ for $p\in (1,2]$. Our bounds considerably improve previous bounds due to (Woodruff et al. COLT, 2013) and (Vempala et al., SODA, 2020).

Learning the Positions in CountSketch

We consider sketching algorithms which first compress data by multiplication with a random sketch matrix, and then apply the sketch to quickly solve an optimization problem, e.g., low-rank approximation and regression. In the learning-based sketching paradigm proposed by~\cite{indyk2019learning}, the sketch matrix is found by choosing a random sparse matrix, e.g., CountSketch, and then the values of its non-zero entries are updated by running gradient descent on a training data set. Despite the growing body of work on this paradigm, a noticeable omission is that the locations of the non-zero entries of previous algorithms were fixed, and only their values were learned. In this work, we propose the first learning-based algorithms that also optimize the locations of the non-zero entries. Our first proposed algorithm is based on a greedy algorithm. However, one drawback of the greedy algorithm is its slower training time. We fix this issue and propose approaches for learning a sketching matrix for both low-rank approximation and Hessian approximation for second order optimization. The latter is helpful for a range of constrained optimization problems, such as LASSO and matrix estimation with a nuclear norm constraint. Both approaches achieve good accuracy with a fast running time. Moreover, our experiments suggest that our algorithm can still reduce the error significantly even if we only have a very limited number of training matrices.

Triangle and Four Cycle Counting with Predictions in Graph Streams

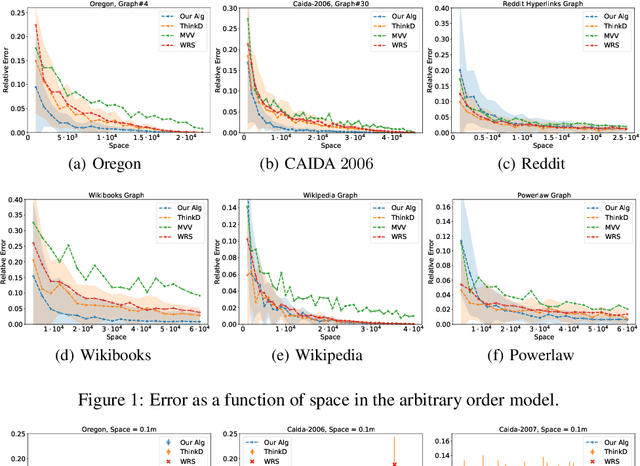
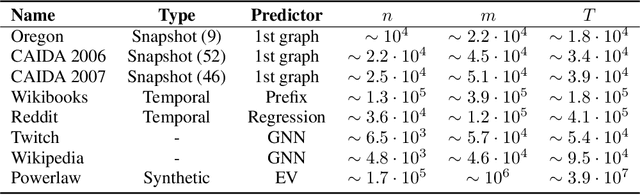
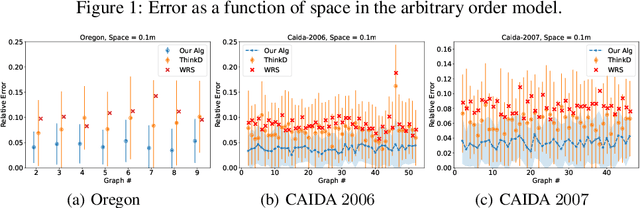
We propose data-driven one-pass streaming algorithms for estimating the number of triangles and four cycles, two fundamental problems in graph analytics that are widely studied in the graph data stream literature. Recently, (Hsu 2018) and (Jiang 2020) applied machine learning techniques in other data stream problems, using a trained oracle that can predict certain properties of the stream elements to improve on prior "classical" algorithms that did not use oracles. In this paper, we explore the power of a "heavy edge" oracle in multiple graph edge streaming models. In the adjacency list model, we present a one-pass triangle counting algorithm improving upon the previous space upper bounds without such an oracle. In the arbitrary order model, we present algorithms for both triangle and four cycle estimation with fewer passes and the same space complexity as in previous algorithms, and we show several of these bounds are optimal. We analyze our algorithms under several noise models, showing that the algorithms perform well even when the oracle errs. Our methodology expands upon prior work on "classical" streaming algorithms, as previous multi-pass and random order streaming algorithms can be seen as special cases of our algorithms, where the first pass or random order was used to implement the heavy edge oracle. Lastly, our experiments demonstrate advantages of the proposed method compared to state-of-the-art streaming algorithms.

Robust Learning of Fixed-Structure Bayesian Networks in Nearly-Linear Time

We study the problem of learning Bayesian networks where an $\epsilon$-fraction of the samples are adversarially corrupted. We focus on the fully-observable case where the underlying graph structure is known. In this work, we present the first nearly-linear time algorithm for this problem with a dimension-independent error guarantee. Previous robust algorithms with comparable error guarantees are slower by at least a factor of $(d/\epsilon)$, where $d$ is the number of variables in the Bayesian network and $\epsilon$ is the fraction of corrupted samples. Our algorithm and analysis are considerably simpler than those in previous work. We achieve this by establishing a direct connection between robust learning of Bayesian networks and robust mean estimation. As a subroutine in our algorithm, we develop a robust mean estimation algorithm whose runtime is nearly-linear in the number of nonzeros in the input samples, which may be of independent interest.

Learning-Augmented Sketches for Hessians

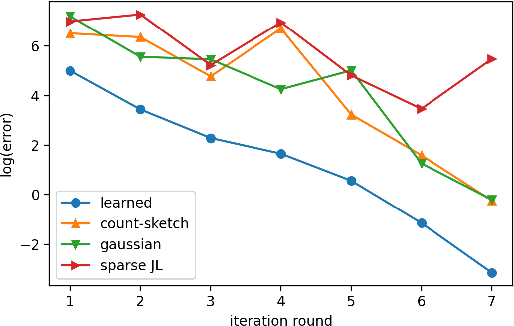
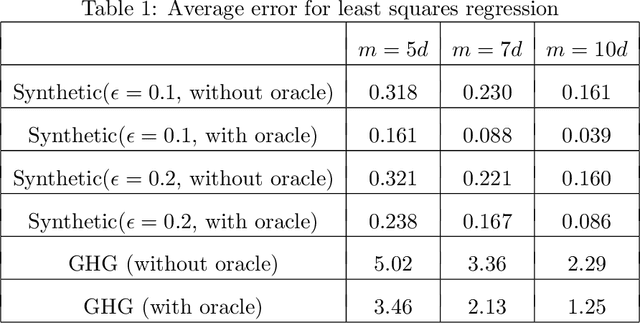
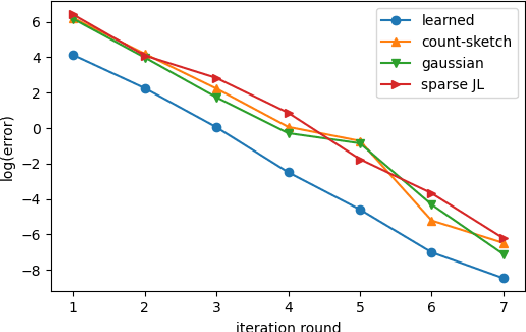
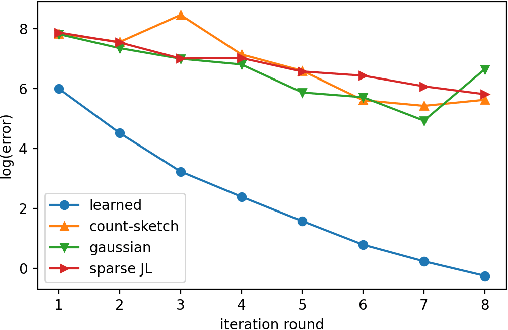
Sketching is a dimensionality reduction technique where one compresses a matrix by linear combinations that are typically chosen at random. A line of work has shown how to sketch the Hessian to speed up each iteration in a second order method, but such sketches usually depend only on the matrix at hand, and in a number of cases are even oblivious to the input matrix. One could instead hope to learn a distribution on sketching matrices that is optimized for the specific distribution of input matrices. We show how to design learned sketches for the Hessian in the context of second order methods, where we learn potentially different sketches for the different iterations of an optimization procedure. We show empirically that learned sketches, compared with their "non-learned" counterparts, improve the approximation accuracy for important problems, including LASSO, SVM, and matrix estimation with nuclear norm constraints. Several of our schemes can be proven to perform no worse than their unlearned counterparts. Additionally, we show that a smaller sketching dimension of the column space of a tall matrix is possible, assuming an oracle for predicting rows which have a large leverage score.