ForecastBench: A Dynamic Benchmark of AI Forecasting Capabilities

Forecasts of future events are essential inputs into informed decision-making. Machine learning (ML) systems have the potential to deliver forecasts at scale, but there is no framework for evaluating the accuracy of ML systems on a standardized set of forecasting questions. To address this gap, we introduce ForecastBench: a dynamic benchmark that evaluates the accuracy of ML systems on an automatically generated and regularly updated set of 1,000 forecasting questions. To avoid any possibility of data leakage, ForecastBench is comprised solely of questions about future events that have no known answer at the time of submission. We quantify the ability of current ML systems by collecting forecasts from expert (human) forecasters, the general public, and LLMs on a random subset of questions from the benchmark (N = 200). While LLMs have achieved super-human performance on many benchmarks, they perform less well here: expert forecasters outperform the top-performing LLM (p-values <= 0.01). We display system and human scores in a public leaderboard at www.forecastbench.org.

Approaching Human-Level Forecasting with Language Models

Forecasting future events is important for policy and decision making. In this work, we study whether language models (LMs) can forecast at the level of competitive human forecasters. Towards this goal, we develop a retrieval-augmented LM system designed to automatically search for relevant information, generate forecasts, and aggregate predictions. To facilitate our study, we collect a large dataset of questions from competitive forecasting platforms. Under a test set published after the knowledge cut-offs of our LMs, we evaluate the end-to-end performance of our system against the aggregates of human forecasts. On average, the system nears the crowd aggregate of competitive forecasters, and in some settings surpasses it. Our work suggests that using LMs to forecast the future could provide accurate predictions at scale and help to inform institutional decision making.

Adaptive Regret for Bandits Made Possible: Two Queries Suffice

Fast changing states or volatile environments pose a significant challenge to online optimization, which needs to perform rapid adaptation under limited observation. In this paper, we give query and regret optimal bandit algorithms under the strict notion of strongly adaptive regret, which measures the maximum regret over any contiguous interval $I$. Due to its worst-case nature, there is an almost-linear $\Omega(|I|^{1-\epsilon})$ regret lower bound, when only one query per round is allowed [Daniely el al, ICML 2015]. Surprisingly, with just two queries per round, we give Strongly Adaptive Bandit Learner (StABL) that achieves $\tilde{O}(\sqrt{n|I|})$ adaptive regret for multi-armed bandits with $n$ arms. The bound is tight and cannot be improved in general. Our algorithm leverages a multiplicative update scheme of varying stepsizes and a carefully chosen observation distribution to control the variance. Furthermore, we extend our results and provide optimal algorithms in the bandit convex optimization setting. Finally, we empirically demonstrate the superior performance of our algorithms under volatile environments and for downstream tasks, such as algorithm selection for hyperparameter optimization.

Constant Approximation for Individual Preference Stable Clustering

Individual preference (IP) stability, introduced by Ahmadi et al. (ICML 2022), is a natural clustering objective inspired by stability and fairness constraints. A clustering is $\alpha$-IP stable if the average distance of every data point to its own cluster is at most $\alpha$ times the average distance to any other cluster. Unfortunately, determining if a dataset admits a $1$-IP stable clustering is NP-Hard. Moreover, before this work, it was unknown if an $o(n)$-IP stable clustering always \emph{exists}, as the prior state of the art only guaranteed an $O(n)$-IP stable clustering. We close this gap in understanding and show that an $O(1)$-IP stable clustering always exists for general metrics, and we give an efficient algorithm which outputs such a clustering. We also introduce generalizations of IP stability beyond average distance and give efficient, near-optimal algorithms in the cases where we consider the maximum and minimum distances within and between clusters.

Towards Best Practices of Activation Patching in Language Models: Metrics and Methods

Mechanistic interpretability seeks to understand the internal mechanisms of machine learning models, where localization -- identifying the important model components -- is a key step. Activation patching, also known as causal tracing or interchange intervention, is a standard technique for this task (Vig et al., 2020), but the literature contains many variants with little consensus on the choice of hyperparameters or methodology. In this work, we systematically examine the impact of methodological details in activation patching, including evaluation metrics and corruption methods. In several settings of localization and circuit discovery in language models, we find that varying these hyperparameters could lead to disparate interpretability results. Backed by empirical observations, we give conceptual arguments for why certain metrics or methods may be preferred. Finally, we provide recommendations for the best practices of activation patching going forwards.

Streaming Algorithms for Learning with Experts: Deterministic Versus Robust

In the online learning with experts problem, an algorithm must make a prediction about an outcome on each of $T$ days (or times), given a set of $n$ experts who make predictions on each day (or time). The algorithm is given feedback on the outcomes of each day, including the cost of its prediction and the cost of the expert predictions, and the goal is to make a prediction with the minimum cost, specifically compared to the best expert in the set. Recent work by Srinivas, Woodruff, Xu, and Zhou (STOC 2022) introduced the study of the online learning with experts problem under memory constraints. However, often the predictions made by experts or algorithms at some time influence future outcomes, so that the input is adaptively chosen. Whereas deterministic algorithms would be robust to adaptive inputs, existing algorithms all crucially use randomization to sample a small number of experts. In this paper, we study deterministic and robust algorithms for the experts problem. We first show a space lower bound of $\widetilde{\Omega}\left(\frac{nM}{RT}\right)$ for any deterministic algorithm that achieves regret $R$ when the best expert makes $M$ mistakes. Our result shows that the natural deterministic algorithm, which iterates through pools of experts until each expert in the pool has erred, is optimal up to polylogarithmic factors. On the positive side, we give a randomized algorithm that is robust to adaptive inputs that uses $\widetilde{O}\left(\frac{n}{R\sqrt{T}}\right)$ space for $M=O\left(\frac{R^2 T}{\log^2 n}\right)$, thereby showing a smooth space-regret trade-off.

Privately Estimating a Gaussian: Efficient, Robust and Optimal

In this work, we give efficient algorithms for privately estimating a Gaussian distribution in both pure and approximate differential privacy (DP) models with optimal dependence on the dimension in the sample complexity. In the pure DP setting, we give an efficient algorithm that estimates an unknown $d$-dimensional Gaussian distribution up to an arbitrary tiny total variation error using $\widetilde{O}(d^2 \log \kappa)$ samples while tolerating a constant fraction of adversarial outliers. Here, $\kappa$ is the condition number of the target covariance matrix. The sample bound matches best non-private estimators in the dependence on the dimension (up to a polylogarithmic factor). We prove a new lower bound on differentially private covariance estimation to show that the dependence on the condition number $\kappa$ in the above sample bound is also tight. Prior to our work, only identifiability results (yielding inefficient super-polynomial time algorithms) were known for the problem. In the approximate DP setting, we give an efficient algorithm to estimate an unknown Gaussian distribution up to an arbitrarily tiny total variation error using $\widetilde{O}(d^2)$ samples while tolerating a constant fraction of adversarial outliers. Prior to our work, all efficient approximate DP algorithms incurred a super-quadratic sample cost or were not outlier-robust. For the special case of mean estimation, our algorithm achieves the optimal sample complexity of $\widetilde O(d)$, improving on a $\widetilde O(d^{1.5})$ bound from prior work. Our pure DP algorithm relies on a recursive private preconditioning subroutine that utilizes the recent work on private mean estimation [Hopkins et al., 2022]. Our approximate DP algorithms are based on a substantial upgrade of the method of stabilizing convex relaxations introduced in [Kothari et al., 2022].

Optimal Query Complexities for Dynamic Trace Estimation

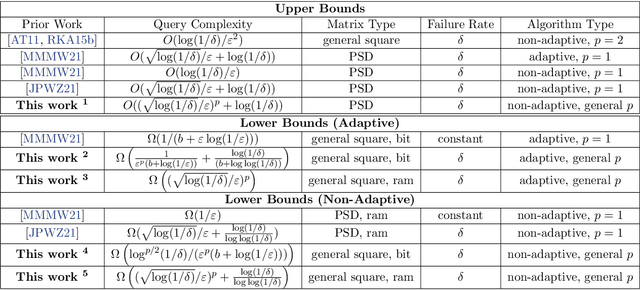
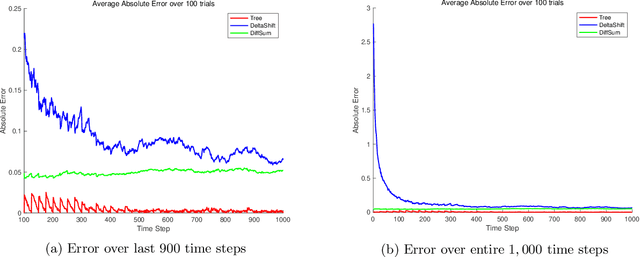
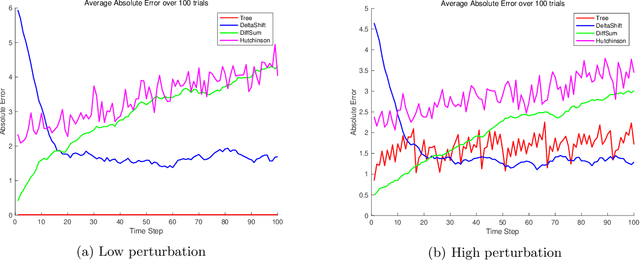
We consider the problem of minimizing the number of matrix-vector queries needed for accurate trace estimation in the dynamic setting where our underlying matrix is changing slowly, such as during an optimization process. Specifically, for any $m$ matrices $A_1,...,A_m$ with consecutive differences bounded in Schatten-$1$ norm by $\alpha$, we provide a novel binary tree summation procedure that simultaneously estimates all $m$ traces up to $\epsilon$ error with $\delta$ failure probability with an optimal query complexity of $\widetilde{O}\left(m \alpha\sqrt{\log(1/\delta)}/\epsilon + m\log(1/\delta)\right)$, improving the dependence on both $\alpha$ and $\delta$ from Dharangutte and Musco (NeurIPS, 2021). Our procedure works without additional norm bounds on $A_i$ and can be generalized to a bound for the $p$-th Schatten norm for $p \in [1,2]$, giving a complexity of $\widetilde{O}\left(m \alpha\left(\sqrt{\log(1/\delta)}/\epsilon\right)^p +m \log(1/\delta)\right)$. By using novel reductions to communication complexity and information-theoretic analyses of Gaussian matrices, we provide matching lower bounds for static and dynamic trace estimation in all relevant parameters, including the failure probability. Our lower bounds (1) give the first tight bounds for Hutchinson's estimator in the matrix-vector product model with Frobenius norm error even in the static setting, and (2) are the first unconditional lower bounds for dynamic trace estimation, resolving open questions of prior work.

Online Prediction in Sub-linear Space

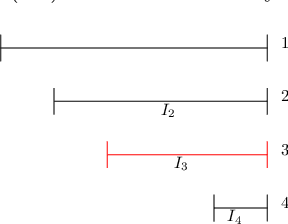
We provide the first sub-linear space and sub-linear regret algorithm for online learning with expert advice (against an oblivious adversary), addressing an open question raised recently by Srinivas, Woodruff, Xu and Zhou (STOC 2022). We also demonstrate a separation between oblivious and (strong) adaptive adversaries by proving a linear memory lower bound of any sub-linear regret algorithm against an adaptive adversary. Our algorithm is based on a novel pool selection procedure that bypasses the traditional wisdom of leader selection for online learning, and a generic reduction that transforms any weakly sub-linear regret $o(T)$ algorithm to $T^{1-\alpha}$ regret algorithm, which may be of independent interest. Our lower bound utilizes the connection of no-regret learning and equilibrium computation in zero-sum games, leading to a proof of a strong lower bound against an adaptive adversary.

Optimal Robustness-Consistency Trade-offs for Learning-Augmented Online Algorithms

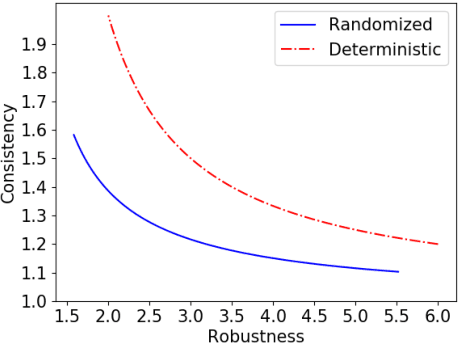
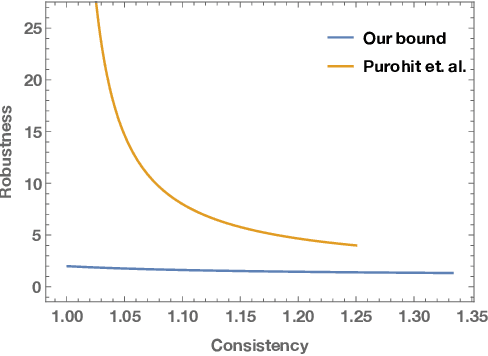
We study the problem of improving the performance of online algorithms by incorporating machine-learned predictions. The goal is to design algorithms that are both consistent and robust, meaning that the algorithm performs well when predictions are accurate and maintains worst-case guarantees. Such algorithms have been studied in a recent line of works due to Lykouris and Vassilvitskii (ICML '18) and Purohit et al (NeurIPS '18). They provide robustness-consistency trade-offs for a variety of online problems. However, they leave open the question of whether these trade-offs are tight, i.e., to what extent to such trade-offs are necessary. In this paper, we provide the first set of non-trivial lower bounds for competitive analysis using machine-learned predictions. We focus on the classic problems of ski-rental and non-clairvoyant scheduling and provide optimal trade-offs in various settings.