Scalable Learning of Multivariate Distributions via Coresets

Efficient and scalable non-parametric or semi-parametric regression analysis and density estimation are of crucial importance to the fields of statistics and machine learning. However, available methods are limited in their ability to handle large-scale data. We address this issue by developing a novel coreset construction for multivariate conditional transformation models (MCTMs) to enhance their scalability and training efficiency. To the best of our knowledge, these are the first coresets for semi-parametric distributional models. Our approach yields substantial data reduction via importance sampling. It ensures with high probability that the log-likelihood remains within multiplicative error bounds of $(1\pm\varepsilon)$ and thereby maintains statistical model accuracy. Compared to conventional full-parametric models, where coresets have been incorporated before, our semi-parametric approach exhibits enhanced adaptability, particularly in scenarios where complex distributions and non-linear relationships are present, but not fully understood. To address numerical problems associated with normalizing logarithmic terms, we follow a geometric approximation based on the convex hull of input data. This ensures feasible, stable, and accurate inference in scenarios involving large amounts of data. Numerical experiments demonstrate substantially improved computational efficiency when handling large and complex datasets, thus laying the foundation for a broad range of applications within the statistics and machine learning communities.

Hardness of High-Dimensional Linear Classification

We establish new exponential in dimension lower bounds for the Maximum Halfspace Discrepancy problem, which models linear classification. Both are fundamental problems in computational geometry and machine learning in their exact and approximate forms. However, only $O(n^d)$ and respectively $\tilde O(1/\varepsilon^d)$ upper bounds are known and complemented by polynomial lower bounds that do not support the exponential in dimension dependence. We close this gap up to polylogarithmic terms by reduction from widely-believed hardness conjectures for Affine Degeneracy testing and $k$-Sum problems. Our reductions yield matching lower bounds of $\tildeΩ(n^d)$ and respectively $\tildeΩ(1/\varepsilon^d)$ based on Affine Degeneracy testing, and $\tildeΩ(n^{d/2})$ and respectively $\tildeΩ(1/\varepsilon^{d/2})$ conditioned on $k$-Sum. The first bound also holds unconditionally if the computational model is restricted to make sidedness queries, which corresponds to a widely spread setting implemented and optimized in many contemporary algorithms and computing paradigms.

Almost Linear Constant-Factor Sketching for $\ell_1$ and Logistic Regression

We improve upon previous oblivious sketching and turnstile streaming results for $\ell_1$ and logistic regression, giving a much smaller sketching dimension achieving $O(1)$-approximation and yielding an efficient optimization problem in the sketch space. Namely, we achieve for any constant $c>0$ a sketching dimension of $\tilde{O}(d^{1+c})$ for $\ell_1$ regression and $\tilde{O}(\mu d^{1+c})$ for logistic regression, where $\mu$ is a standard measure that captures the complexity of compressing the data. For $\ell_1$-regression our sketching dimension is near-linear and improves previous work which either required $\Omega(\log d)$-approximation with this sketching dimension, or required a larger $\operatorname{poly}(d)$ number of rows. Similarly, for logistic regression previous work had worse $\operatorname{poly}(\mu d)$ factors in its sketching dimension. We also give a tradeoff that yields a $1+\varepsilon$ approximation in input sparsity time by increasing the total size to $(d\log(n)/\varepsilon)^{O(1/\varepsilon)}$ for $\ell_1$ and to $(\mu d\log(n)/\varepsilon)^{O(1/\varepsilon)}$ for logistic regression. Finally, we show that our sketch can be extended to approximate a regularized version of logistic regression where the data-dependent regularizer corresponds to the variance of the individual logistic losses.

Bounding the Width of Neural Networks via Coupled Initialization -- A Worst Case Analysis

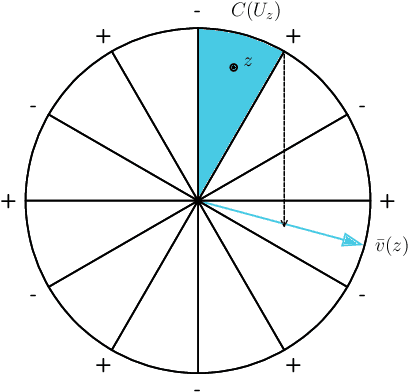
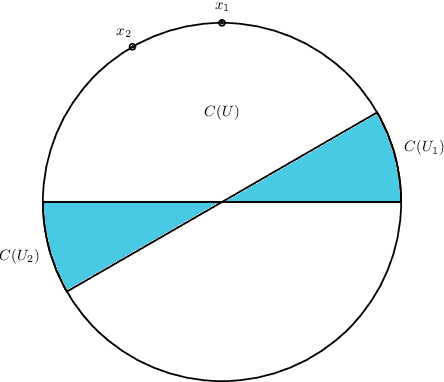
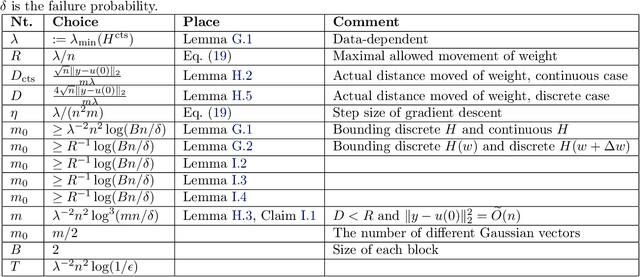
A common method in training neural networks is to initialize all the weights to be independent Gaussian vectors. We observe that by instead initializing the weights into independent pairs, where each pair consists of two identical Gaussian vectors, we can significantly improve the convergence analysis. While a similar technique has been studied for random inputs [Daniely, NeurIPS 2020], it has not been analyzed with arbitrary inputs. Using this technique, we show how to significantly reduce the number of neurons required for two-layer ReLU networks, both in the under-parameterized setting with logistic loss, from roughly $\gamma^{-8}$ [Ji and Telgarsky, ICLR 2020] to $\gamma^{-2}$, where $\gamma$ denotes the separation margin with a Neural Tangent Kernel, as well as in the over-parameterized setting with squared loss, from roughly $n^4$ [Song and Yang, 2019] to $n^2$, implicitly also improving the recent running time bound of [Brand, Peng, Song and Weinstein, ITCS 2021]. For the under-parameterized setting we also prove new lower bounds that improve upon prior work, and that under certain assumptions, are best possible.

$p$-Generalized Probit Regression and Scalable Maximum Likelihood Estimation via Sketching and Coresets

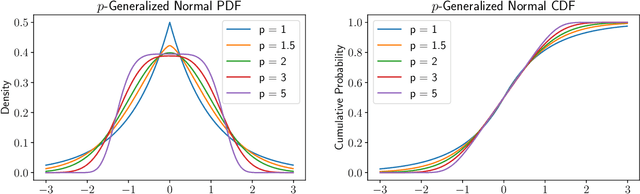
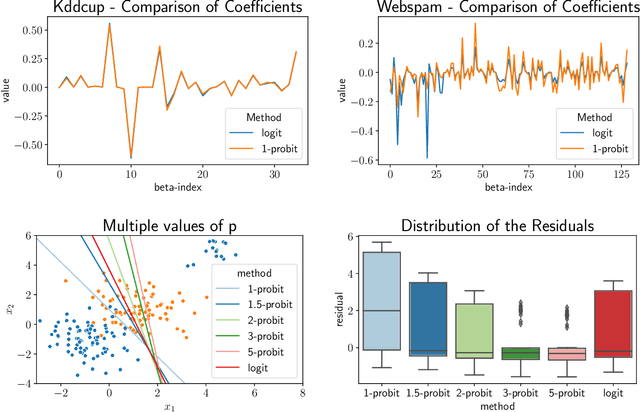
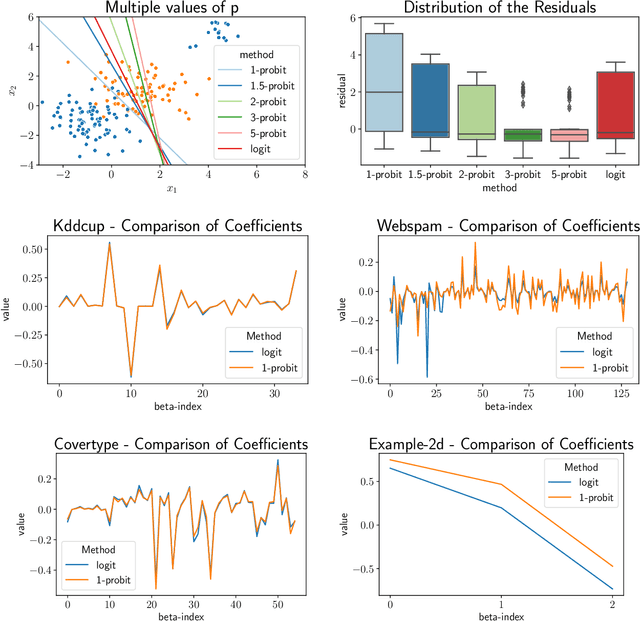
We study the $p$-generalized probit regression model, which is a generalized linear model for binary responses. It extends the standard probit model by replacing its link function, the standard normal cdf, by a $p$-generalized normal distribution for $p\in[1, \infty)$. The $p$-generalized normal distributions \citep{Sub23} are of special interest in statistical modeling because they fit much more flexibly to data. Their tail behavior can be controlled by choice of the parameter $p$, which influences the model's sensitivity to outliers. Special cases include the Laplace, the Gaussian, and the uniform distributions. We further show how the maximum likelihood estimator for $p$-generalized probit regression can be approximated efficiently up to a factor of $(1+\varepsilon)$ on large data by combining sketching techniques with importance subsampling to obtain a small data summary called coreset.

Oblivious sketching for logistic regression

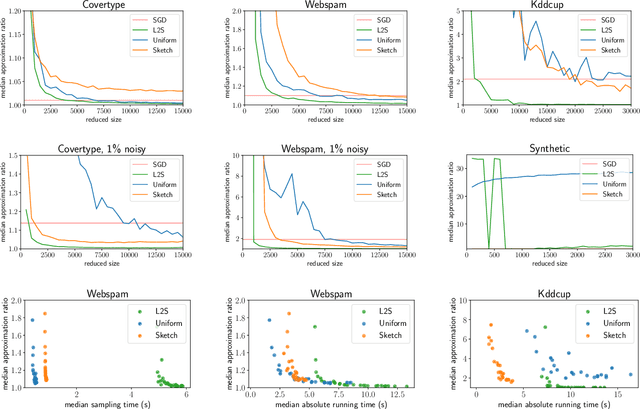
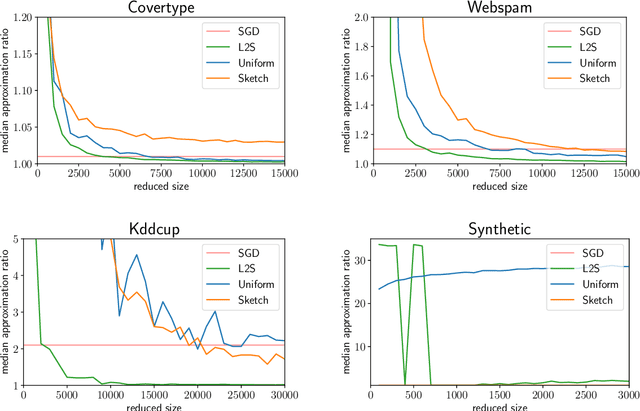
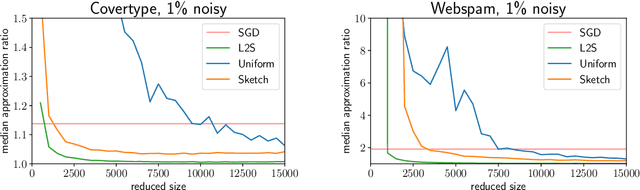
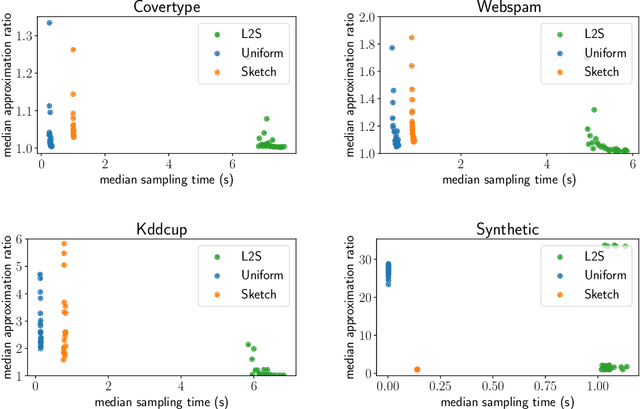
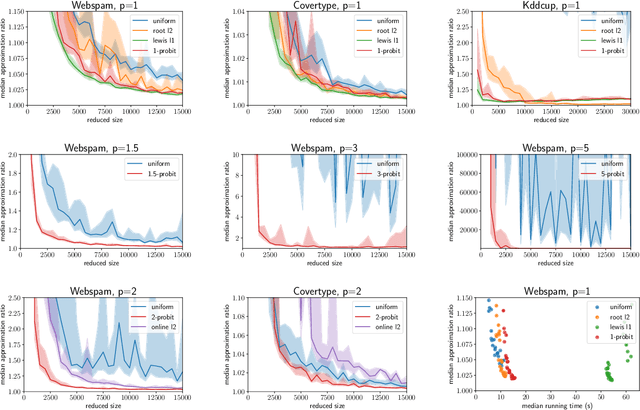
What guarantees are possible for solving logistic regression in one pass over a data stream? To answer this question, we present the first data oblivious sketch for logistic regression. Our sketch can be computed in input sparsity time over a turnstile data stream and reduces the size of a $d$-dimensional data set from $n$ to only $\operatorname{poly}(\mu d\log n)$ weighted points, where $\mu$ is a useful parameter which captures the complexity of compressing the data. Solving (weighted) logistic regression on the sketch gives an $O(\log n)$-approximation to the original problem on the full data set. We also show how to obtain an $O(1)$-approximation with slight modifications. Our sketches are fast, simple, easy to implement, and our experiments demonstrate their practicality.