Cho-Jui Hsieh
Robustness Verification of Tree-based Models
Jun 15, 2019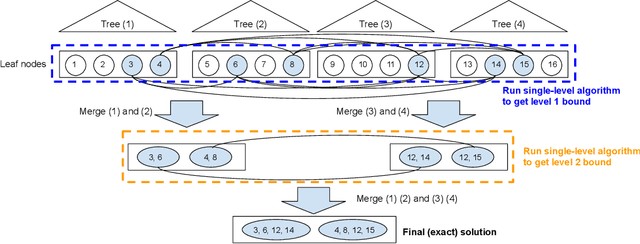
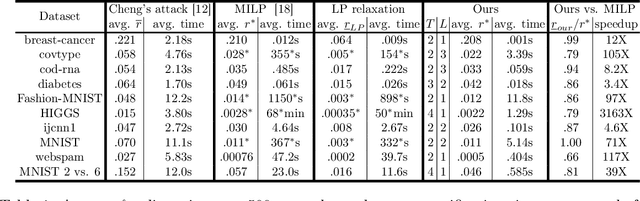
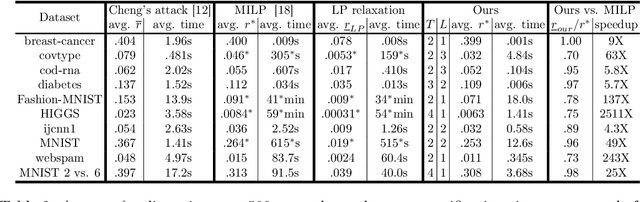
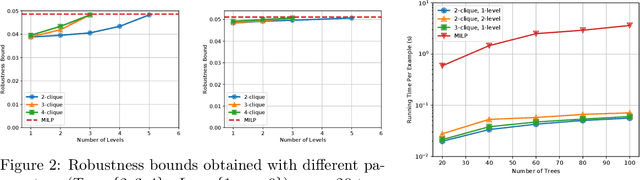
Abstract:We study the robustness verification problem for tree-based models, including decision trees, random forests (RFs) and gradient boosted decision trees (GBDTs). Formal robustness verification of decision tree ensembles involves finding the exact minimal adversarial perturbation or a guaranteed lower bound of it. Existing approaches find the minimal adversarial perturbation by a mixed integer linear programming (MILP) problem, which takes exponential time so is impractical for large ensembles. Although this verification problem is NP-complete in general, we give a more precise complexity characterization. We show that there is a simple linear time algorithm for verifying a single tree, and for tree ensembles, the verification problem can be cast as a max-clique problem on a multi-partite graph with bounded boxicity. For low dimensional problems when boxicity can be viewed as constant, this reformulation leads to a polynomial time algorithm. For general problems, by exploiting the boxicity of the graph, we develop an efficient multi-level verification algorithm that can give tight lower bounds on the robustness of decision tree ensembles, while allowing iterative improvement and any-time termination. OnRF/GBDT models trained on 10 datasets, our algorithm is hundreds of times faster than the previous approach that requires solving MILPs, and is able to give tight robustness verification bounds on large GBDTs with hundreds of deep trees.
Towards Stable and Efficient Training of Verifiably Robust Neural Networks
Jun 14, 2019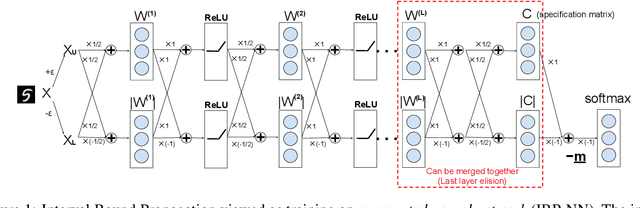
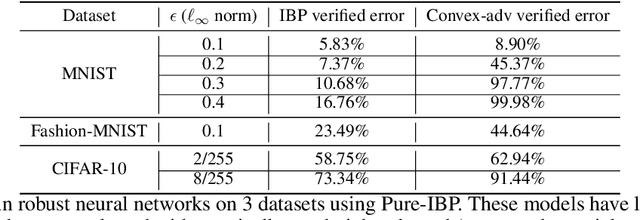
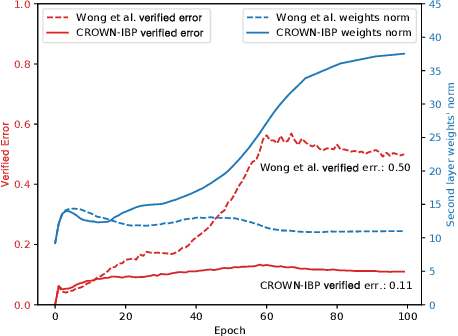
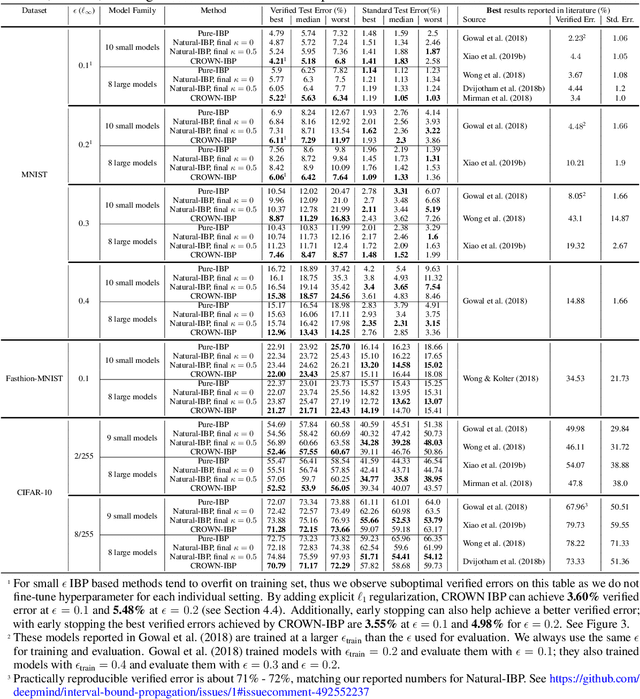
Abstract:Training neural networks with verifiable robustness guarantees is challenging. Several existing successful approaches utilize relatively tight linear relaxation based bounds of neural network outputs, but they can slow down training by a factor of hundreds and over-regularize the network. Meanwhile, interval bound propagation (IBP) based training is efficient and significantly outperform linear relaxation based methods on some tasks, yet it suffers from stability issues since the bounds are much looser. In this paper, we first interpret IBP training as training an augmented network which computes non-linear bounds, thus explaining its good performance. We then propose a new certified adversarial training method, CROWN-IBP, by combining the fast IBP bounds in the forward pass and a tight linear relaxation based bound, CROWN, in the backward pass. The proposed method is computationally efficient and consistently outperforms IBP baselines on training verifiably robust neural networks. We conduct large scale experiments using 53 models on MNIST, Fashion-MNIST and CIFAR datasets. On MNIST with $\epsilon=0.3$ and $\epsilon=0.4$ ($\ell_\infty$ norm distortion) we achieve 7.46\% and 12.96\% verified error on test set, respectively, outperforming previous certified defense methods.
Evaluating the Robustness of Nearest Neighbor Classifiers: A Primal-Dual Perspective
Jun 10, 2019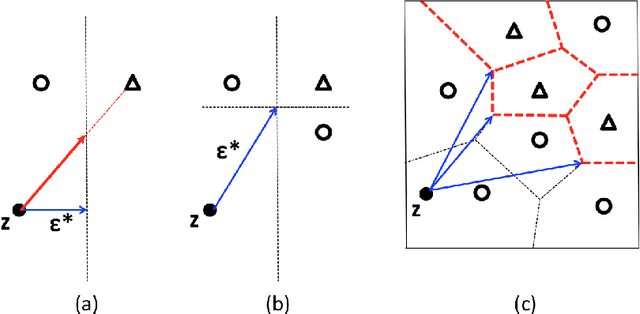
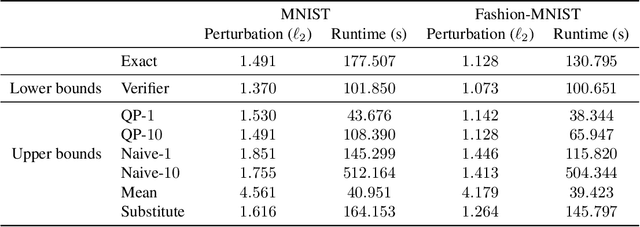
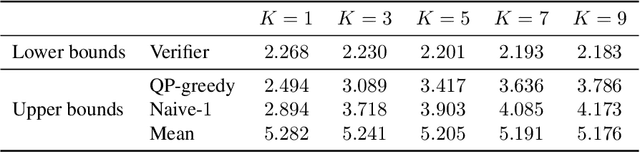
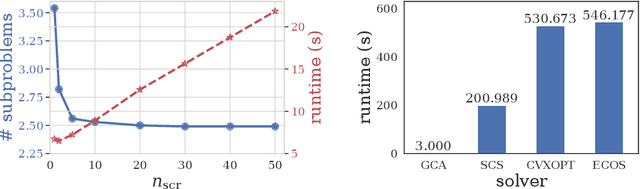
Abstract:We study the problem of computing the minimum adversarial perturbation of the Nearest Neighbor (NN) classifiers. Previous attempts either conduct attacks on continuous approximations of NN models or search for the perturbation by some heuristic methods. In this paper, we propose the first algorithm that is able to compute the minimum adversarial perturbation. The main idea is to formulate the problem as a list of convex quadratic programming (QP) problems that can be efficiently solved by the proposed algorithms for 1-NN models. Furthermore, we show that dual solutions for these QP problems could give us a valid lower bound of the adversarial perturbation that can be used for formal robustness verification, giving us a nice view of attack/verification for NN models. For $K$-NN models with larger $K$, we show that the same formulation can help us efficiently compute the upper and lower bounds of the minimum adversarial perturbation, which can be used for attack and verification.
ML-LOO: Detecting Adversarial Examples with Feature Attribution
Jun 08, 2019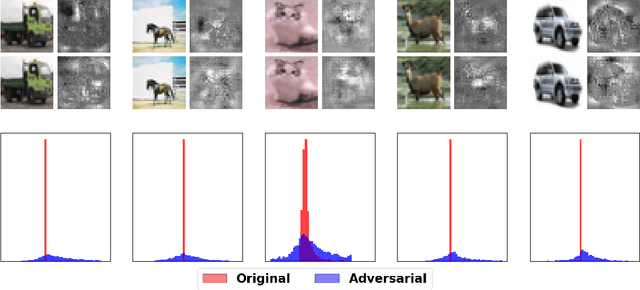
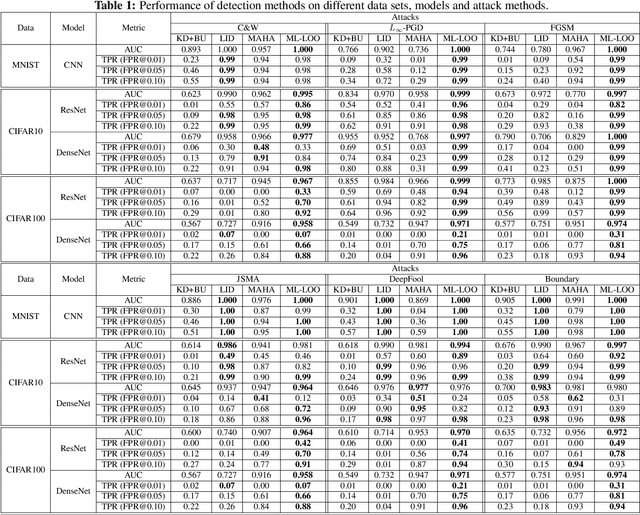
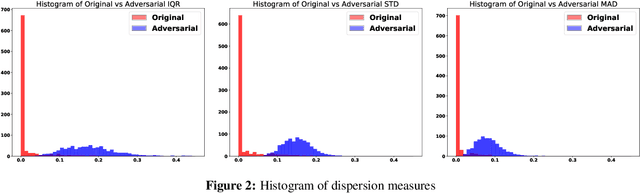
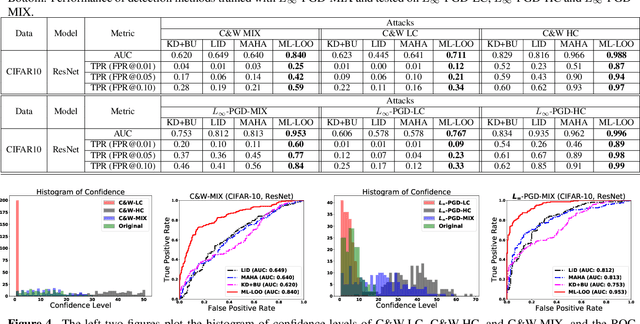
Abstract:Deep neural networks obtain state-of-the-art performance on a series of tasks. However, they are easily fooled by adding a small adversarial perturbation to input. The perturbation is often human imperceptible on image data. We observe a significant difference in feature attributions of adversarially crafted examples from those of original ones. Based on this observation, we introduce a new framework to detect adversarial examples through thresholding a scale estimate of feature attribution scores. Furthermore, we extend our method to include multi-layer feature attributions in order to tackle the attacks with mixed confidence levels. Through vast experiments, our method achieves superior performances in distinguishing adversarial examples from popular attack methods on a variety of real data sets among state-of-the-art detection methods. In particular, our method is able to detect adversarial examples of mixed confidence levels, and transfer between different attacking methods.
Neural SDE: Stabilizing Neural ODE Networks with Stochastic Noise
Jun 05, 2019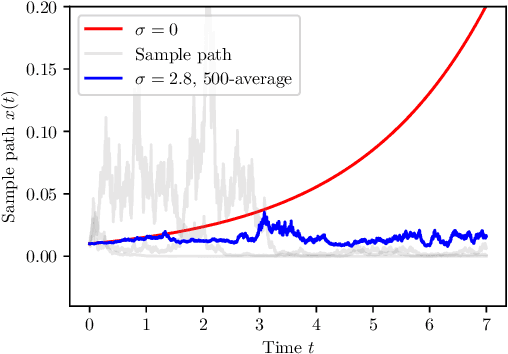

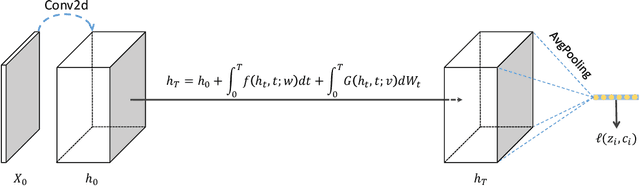
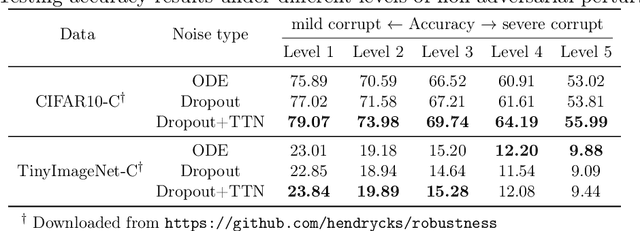
Abstract:Neural Ordinary Differential Equation (Neural ODE) has been proposed as a continuous approximation to the ResNet architecture. Some commonly used regularization mechanisms in discrete neural networks (e.g. dropout, Gaussian noise) are missing in current Neural ODE networks. In this paper, we propose a new continuous neural network framework called Neural Stochastic Differential Equation (Neural SDE) network, which naturally incorporates various commonly used regularization mechanisms based on random noise injection. Our framework can model various types of noise injection frequently used in discrete networks for regularization purpose, such as dropout and additive/multiplicative noise in each block. We provide theoretical analysis explaining the improved robustness of Neural SDE models against input perturbations/adversarial attacks. Furthermore, we demonstrate that the Neural SDE network can achieve better generalization than the Neural ODE and is more resistant to adversarial and non-adversarial input perturbations.
Graph DNA: Deep Neighborhood Aware Graph Encoding for Collaborative Filtering
May 29, 2019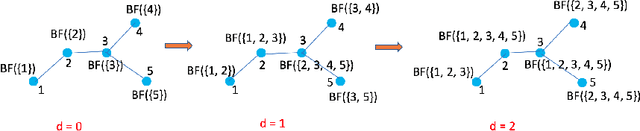
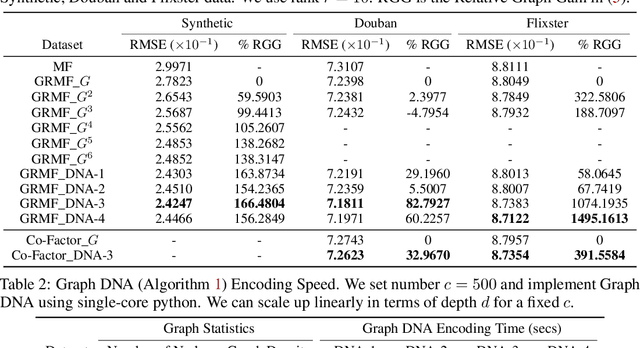
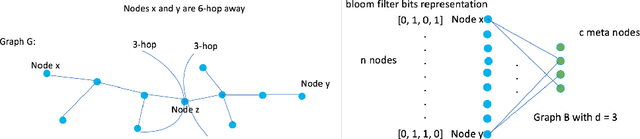

Abstract:In this paper, we consider recommender systems with side information in the form of graphs. Existing collaborative filtering algorithms mainly utilize only immediate neighborhood information and have a hard time taking advantage of deeper neighborhoods beyond 1-2 hops. The main caveat of exploiting deeper graph information is the rapidly growing time and space complexity when incorporating information from these neighborhoods. In this paper, we propose using Graph DNA, a novel Deep Neighborhood Aware graph encoding algorithm, for exploiting deeper neighborhood information. DNA encoding computes approximate deep neighborhood information in linear time using Bloom filters, a space-efficient probabilistic data structure and results in a per-node encoding that is logarithmic in the number of nodes in the graph. It can be used in conjunction with both feature-based and graph-regularization-based collaborative filtering algorithms. Graph DNA has the advantages of being memory and time efficient and providing additional regularization when compared to directly using higher order graph information. We conduct experiments on real-world datasets, showing graph DNA can be easily used with 4 popular collaborative filtering algorithms and consistently leads to a performance boost with little computational and memory overhead.
Stochastic Shared Embeddings: Data-driven Regularization of Embedding Layers
May 25, 2019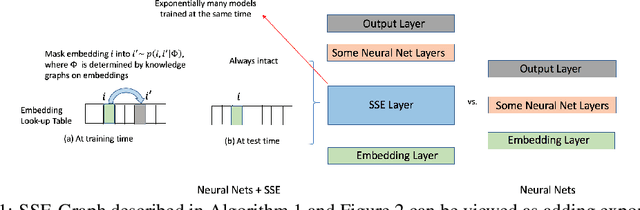

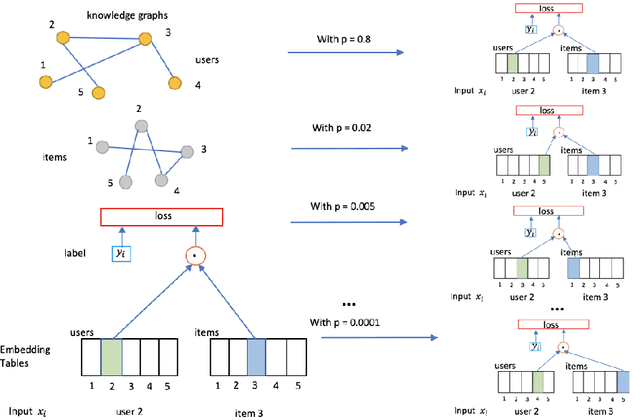
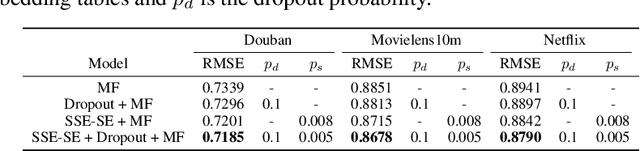
Abstract:In deep neural nets, lower level embedding layers account for a large portion of the total number of parameters. Tikhonov regularization, graph-based regularization, and hard parameter sharing are approaches that introduce explicit biases into training in a hope to reduce statistical complexity. Alternatively, we propose stochastically shared embeddings (SSE), a data-driven approach to regularizing embedding layers, which stochastically transitions between embeddings during stochastic gradient descent (SGD). Because SSE integrates seamlessly with existing SGD algorithms, it can be used with only minor modifications when training large scale neural networks. We develop two versions of SSE: SSE-Graph using knowledge graphs of embeddings; SSE-SE using no prior information. We provide theoretical guarantees for our method and show its empirical effectiveness on 6 distinct tasks, from simple neural networks with one hidden layer in recommender systems, to the transformer and BERT in natural languages. We find that when used along with widely-used regularization methods such as weight decay and dropout, our proposed SSE can further reduce overfitting, which often leads to more favorable generalization results.
Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks
May 20, 2019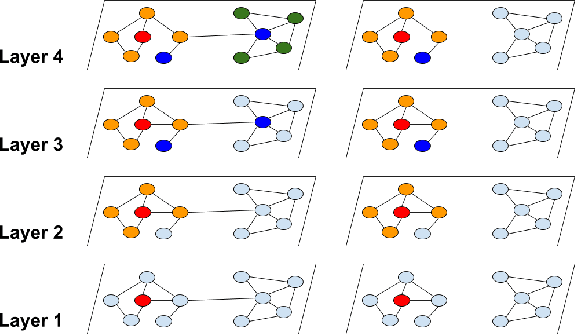
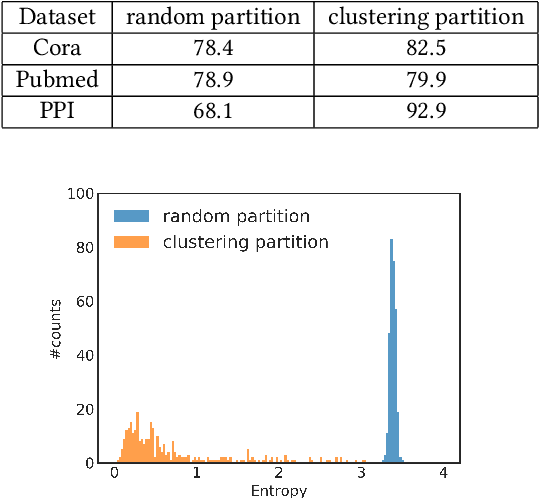
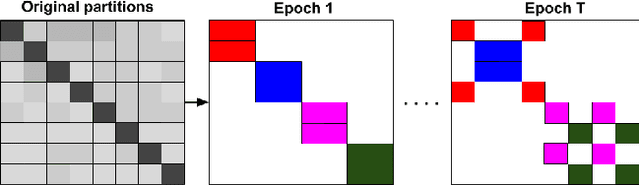
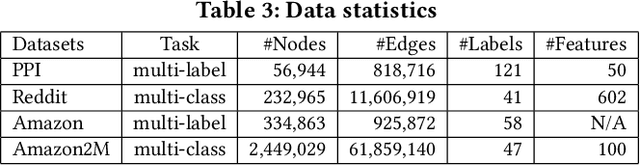
Abstract:Graph convolutional network (GCN) has been successfully applied to many graph-based applications; however, training a large-scale GCN remains challenging. Current SGD-based algorithms suffer from either a high computational cost that exponentially grows with number of GCN layers, or a large space requirement for keeping the entire graph and the embedding of each node in memory. In this paper, we propose Cluster-GCN, a novel GCN algorithm that is suitable for SGD-based training by exploiting the graph clustering structure. Cluster-GCN works as the following: at each step, it samples a block of nodes that associate with a dense subgraph identified by a graph clustering algorithm, and restricts the neighborhood search within this subgraph. This simple but effective strategy leads to significantly improved memory and computational efficiency while being able to achieve comparable test accuracy with previous algorithms. To test the scalability of our algorithm, we create a new Amazon2M data with 2 million nodes and 61 million edges which is more than 5 times larger than the previous largest publicly available dataset (Reddit). For training a 3-layer GCN on this data, Cluster-GCN is faster than the previous state-of-the-art VR-GCN (1523 seconds vs 1961 seconds) and using much less memory (2.2GB vs 11.2GB). Furthermore, for training 4 layer GCN on this data, our algorithm can finish in around 36 minutes while all the existing GCN training algorithms fail to train due to the out-of-memory issue. Furthermore, Cluster-GCN allows us to train much deeper GCN without much time and memory overhead, which leads to improved prediction accuracy---using a 5-layer Cluster-GCN, we achieve state-of-the-art test F1 score 99.36 on the PPI dataset, while the previous best result was 98.71 by [16].
Evaluating Robustness of Deep Image Super-Resolution against Adversarial Attacks
Apr 12, 2019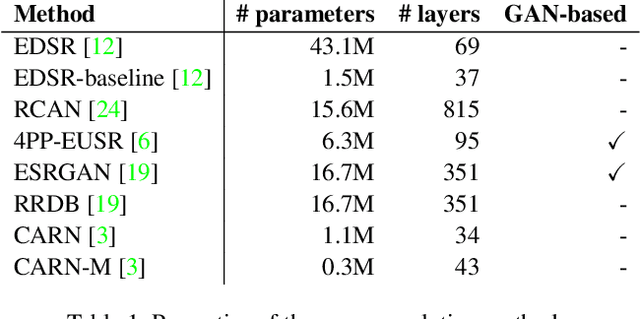
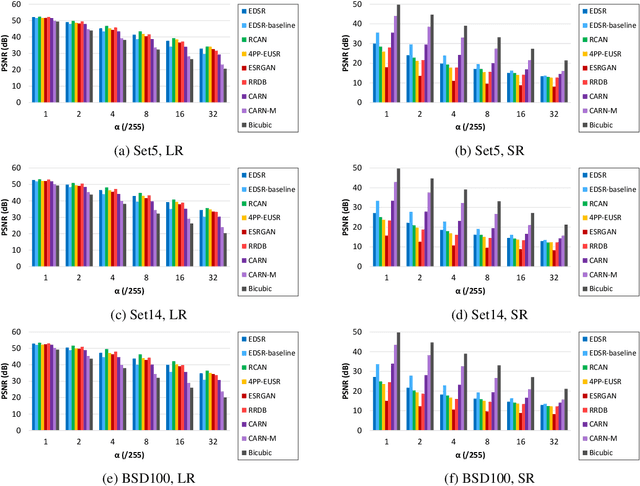

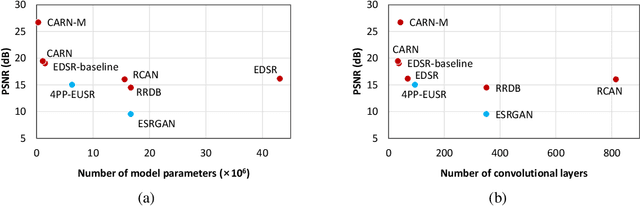
Abstract:Single-image super-resolution aims to generate a high-resolution version of a low-resolution image, which serves as an essential component in many computer vision applications. This paper investigates the robustness of deep learning-based super-resolution methods against adversarial attacks, which can significantly deteriorate the super-resolved images without noticeable distortion in the attacked low-resolution images. It is demonstrated that state-of-the-art deep super-resolution methods are highly vulnerable to adversarial attacks. Different levels of robustness of different methods are analyzed theoretically and experimentally. We also present analysis on transferability of attacks, and feasibility of targeted attacks and universal attacks.
Reducing BERT Pre-Training Time from 3 Days to 76 Minutes
Apr 01, 2019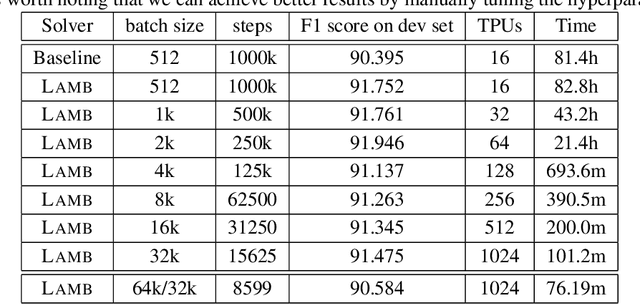
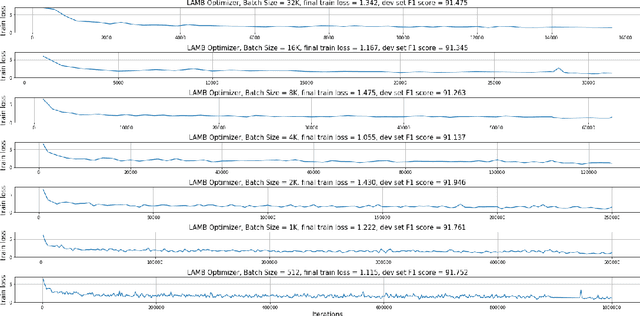
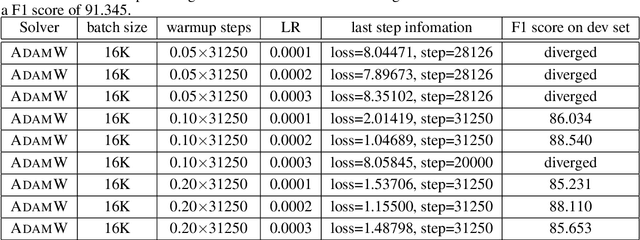
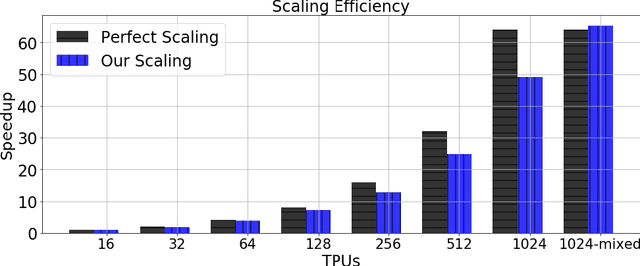
Abstract:Large-batch training is key to speeding up deep neural network training in large distributed systems. However, large-batch training is difficult because it produces a generalization gap. Straightforward optimization often leads to accuracy loss on the test set. BERT \cite{devlin2018bert} is a state-of-the-art deep learning model that builds on top of deep bidirectional transformers for language understanding. Previous large-batch training techniques do not perform well for BERT when we scale the batch size (e.g. beyond 8192). BERT pre-training also takes a long time to finish (around three days on 16 TPUv3 chips). To solve this problem, we propose the LAMB optimizer, which helps us to scale the batch size to 65536 without losing accuracy. LAMB is a general optimizer that works for both small and large batch sizes and does not need hyper-parameter tuning besides the learning rate. The baseline BERT-Large model needs 1 million iterations to finish pre-training, while LAMB with batch size 65536/32768 only needs 8599 iterations. We push the batch size to the memory limit of a TPUv3 pod and can finish BERT training in 76 minutes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge