Hyperbolic Delaunay Geometric Alignment

Hyperbolic machine learning is an emerging field aimed at representing data with a hierarchical structure. However, there is a lack of tools for evaluation and analysis of the resulting hyperbolic data representations. To this end, we propose Hyperbolic Delaunay Geometric Alignment (HyperDGA) -- a similarity score for comparing datasets in a hyperbolic space. The core idea is counting the edges of the hyperbolic Delaunay graph connecting datapoints across the given sets. We provide an empirical investigation on synthetic and real-life biological data and demonstrate that HyperDGA outperforms the hyperbolic version of classical distances between sets. Furthermore, we showcase the potential of HyperDGA for evaluating latent representations inferred by a Hyperbolic Variational Auto-Encoder.

Interactive Perception for Deformable Object Manipulation

Interactive perception enables robots to manipulate the environment and objects to bring them into states that benefit the perception process. Deformable objects pose challenges to this due to significant manipulation difficulty and occlusion in vision-based perception. In this work, we address such a problem with a setup involving both an active camera and an object manipulator. Our approach is based on a sequential decision-making framework and explicitly considers the motion regularity and structure in coupling the camera and manipulator. We contribute a method for constructing and computing a subspace, called Dynamic Active Vision Space (DAVS), for effectively utilizing the regularity in motion exploration. The effectiveness of the framework and approach are validated in both a simulation and a real dual-arm robot setup. Our results confirm the necessity of an active camera and coordinative motion in interactive perception for deformable objects.

Elastic Context: Encoding Elasticity for Data-driven Models of Textiles

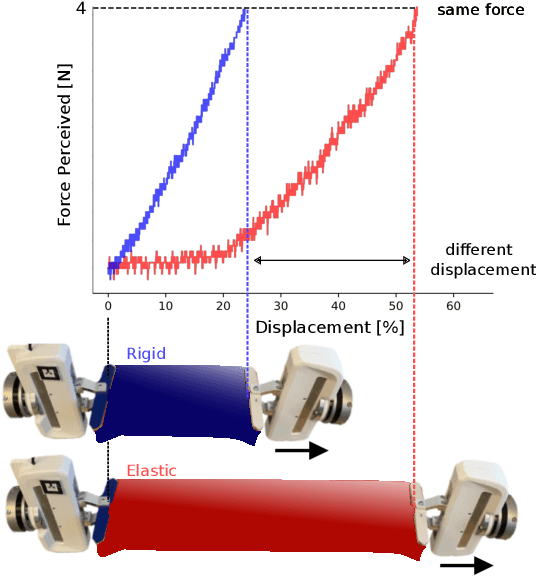
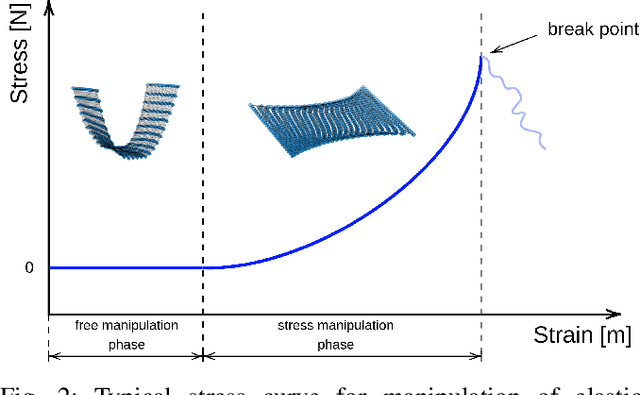
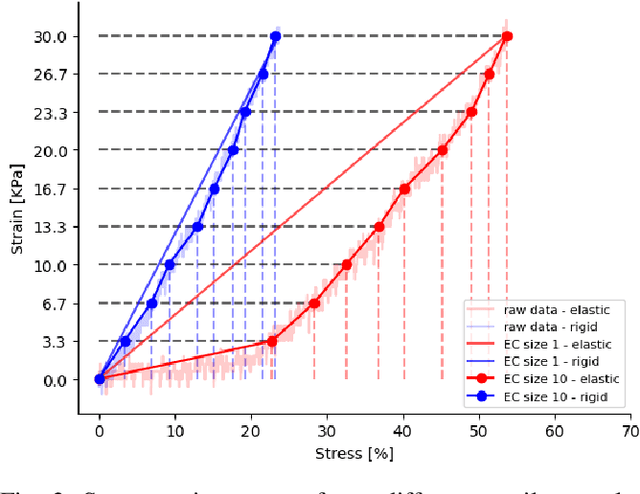
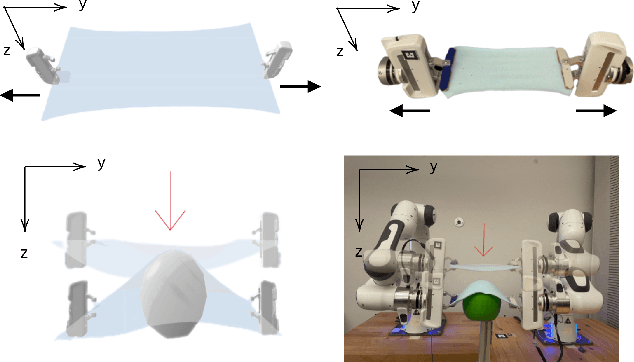
Physical interaction with textiles, such as assistive dressing, relies on advanced dextreous capabilities. The underlying complexity in textile behavior when being pulled and stretched, is due to both the yarn material properties and the textile construction technique. Today, there are no commonly adopted and annotated datasets on which the various interaction or property identification methods are assessed. One important property that affects the interaction is material elasticity that results from both the yarn material and construction technique: these two are intertwined and, if not known a-priori, almost impossible to identify through sensing commonly available on robotic platforms. We introduce Elastic Context (EC), a concept that integrates various properties that affect elastic behavior, to enable a more effective physical interaction with textiles. The definition of EC relies on stress/strain curves commonly used in textile engineering, which we reformulated for robotic applications. We employ EC using Graph Neural Network (GNN) to learn generalized elastic behaviors of textiles. Furthermore, we explore the effect the dimension of the EC has on accurate force modeling of non-linear real-world elastic behaviors, highlighting the challenges of current robotic setups to sense textile properties.

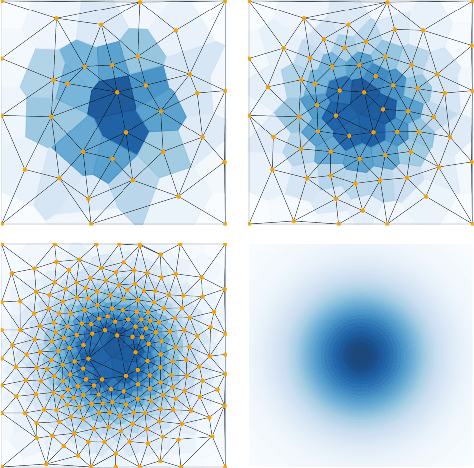
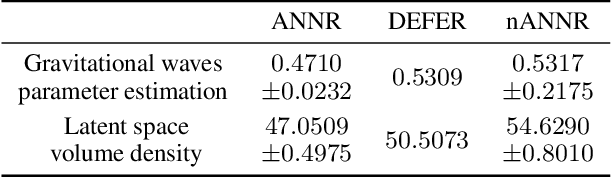
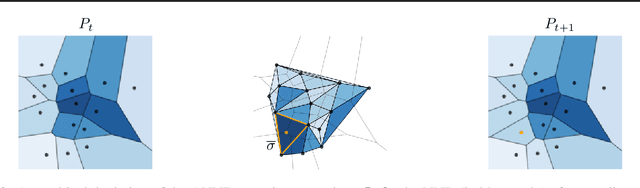
Active Nearest Neighbor Regression Through Delaunay Refinement

We introduce an algorithm for active function approximation based on nearest neighbor regression. Our Active Nearest Neighbor Regressor (ANNR) relies on the Voronoi-Delaunay framework from computational geometry to subdivide the space into cells with constant estimated function value and select novel query points in a way that takes the geometry of the function graph into account. We consider the recent state-of-the-art active function approximator called DEFER, which is based on incremental rectangular partitioning of the space, as the main baseline. The ANNR addresses a number of limitations that arise from the space subdivision strategy used in DEFER. We provide a computationally efficient implementation of our method, as well as theoretical halting guarantees. Empirical results show that ANNR outperforms the baseline for both closed-form functions and real-world examples, such as gravitational wave parameter inference and exploration of the latent space of a generative model.