Hyperbolic Delaunay Geometric Alignment

Hyperbolic machine learning is an emerging field aimed at representing data with a hierarchical structure. However, there is a lack of tools for evaluation and analysis of the resulting hyperbolic data representations. To this end, we propose Hyperbolic Delaunay Geometric Alignment (HyperDGA) -- a similarity score for comparing datasets in a hyperbolic space. The core idea is counting the edges of the hyperbolic Delaunay graph connecting datapoints across the given sets. We provide an empirical investigation on synthetic and real-life biological data and demonstrate that HyperDGA outperforms the hyperbolic version of classical distances between sets. Furthermore, we showcase the potential of HyperDGA for evaluating latent representations inferred by a Hyperbolic Variational Auto-Encoder.

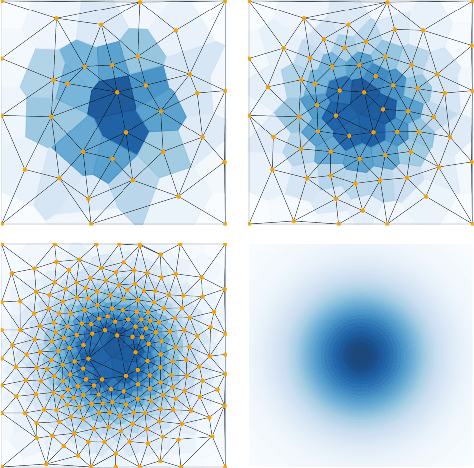
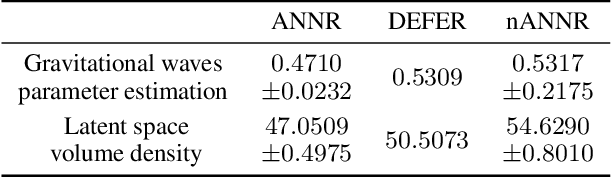
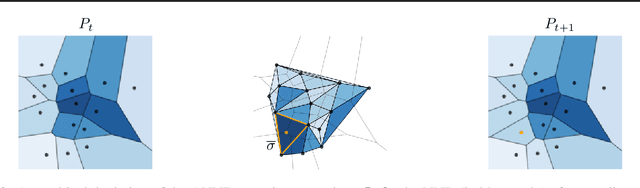
Active Nearest Neighbor Regression Through Delaunay Refinement

We introduce an algorithm for active function approximation based on nearest neighbor regression. Our Active Nearest Neighbor Regressor (ANNR) relies on the Voronoi-Delaunay framework from computational geometry to subdivide the space into cells with constant estimated function value and select novel query points in a way that takes the geometry of the function graph into account. We consider the recent state-of-the-art active function approximator called DEFER, which is based on incremental rectangular partitioning of the space, as the main baseline. The ANNR addresses a number of limitations that arise from the space subdivision strategy used in DEFER. We provide a computationally efficient implementation of our method, as well as theoretical halting guarantees. Empirical results show that ANNR outperforms the baseline for both closed-form functions and real-world examples, such as gravitational wave parameter inference and exploration of the latent space of a generative model.

Delaunay Component Analysis for Evaluation of Data Representations

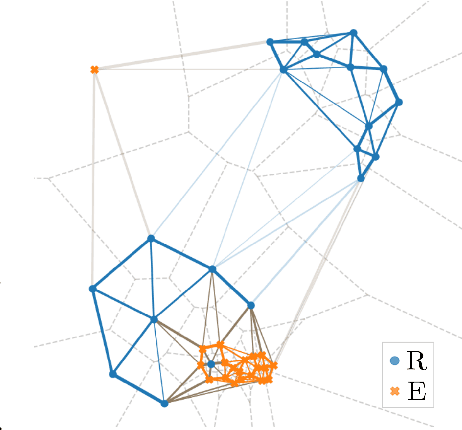
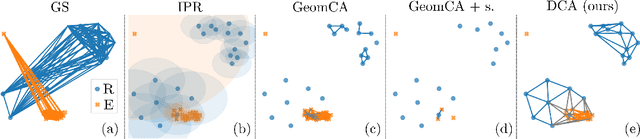
Advanced representation learning techniques require reliable and general evaluation methods. Recently, several algorithms based on the common idea of geometric and topological analysis of a manifold approximated from the learned data representations have been proposed. In this work, we introduce Delaunay Component Analysis (DCA) - an evaluation algorithm which approximates the data manifold using a more suitable neighbourhood graph called Delaunay graph. This provides a reliable manifold estimation even for challenging geometric arrangements of representations such as clusters with varying shape and density as well as outliers, which is where existing methods often fail. Furthermore, we exploit the nature of Delaunay graphs and introduce a framework for assessing the quality of individual novel data representations. We experimentally validate the proposed DCA method on representations obtained from neural networks trained with contrastive objective, supervised and generative models, and demonstrate various use cases of our extended single point evaluation framework.