Hyperbolic Delaunay Geometric Alignment

Hyperbolic machine learning is an emerging field aimed at representing data with a hierarchical structure. However, there is a lack of tools for evaluation and analysis of the resulting hyperbolic data representations. To this end, we propose Hyperbolic Delaunay Geometric Alignment (HyperDGA) -- a similarity score for comparing datasets in a hyperbolic space. The core idea is counting the edges of the hyperbolic Delaunay graph connecting datapoints across the given sets. We provide an empirical investigation on synthetic and real-life biological data and demonstrate that HyperDGA outperforms the hyperbolic version of classical distances between sets. Furthermore, we showcase the potential of HyperDGA for evaluating latent representations inferred by a Hyperbolic Variational Auto-Encoder.

A Robotic Skill Learning System Built Upon Diffusion Policies and Foundation Models

In this paper, we build upon two major recent developments in the field, Diffusion Policies for visuomotor manipulation and large pre-trained multimodal foundational models to obtain a robotic skill learning system. The system can obtain new skills via the behavioral cloning approach of visuomotor diffusion policies given teleoperated demonstrations. Foundational models are being used to perform skill selection given the user's prompt in natural language. Before executing a skill the foundational model performs a precondition check given an observation of the workspace. We compare the performance of different foundational models to this end as well as give a detailed experimental evaluation of the skills taught by the user in simulation and the real world. Finally, we showcase the combined system on a challenging food serving scenario in the real world. Videos of all experimental executions, as well as the process of teaching new skills in simulation and the real world, are available on the project's website.

Delaunay Component Analysis for Evaluation of Data Representations

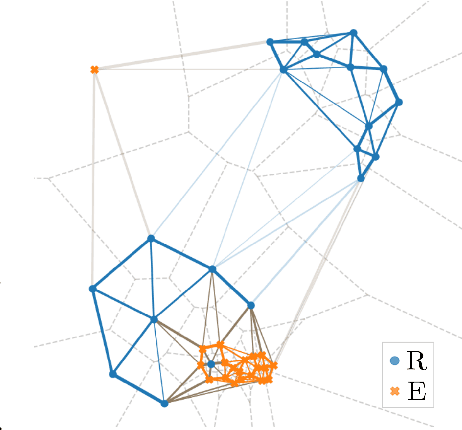
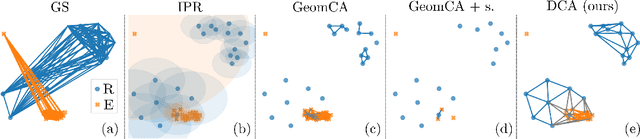
Advanced representation learning techniques require reliable and general evaluation methods. Recently, several algorithms based on the common idea of geometric and topological analysis of a manifold approximated from the learned data representations have been proposed. In this work, we introduce Delaunay Component Analysis (DCA) - an evaluation algorithm which approximates the data manifold using a more suitable neighbourhood graph called Delaunay graph. This provides a reliable manifold estimation even for challenging geometric arrangements of representations such as clusters with varying shape and density as well as outliers, which is where existing methods often fail. Furthermore, we exploit the nature of Delaunay graphs and introduce a framework for assessing the quality of individual novel data representations. We experimentally validate the proposed DCA method on representations obtained from neural networks trained with contrastive objective, supervised and generative models, and demonstrate various use cases of our extended single point evaluation framework.

GraphDCA -- a Framework for Node Distribution Comparison in Real and Synthetic Graphs

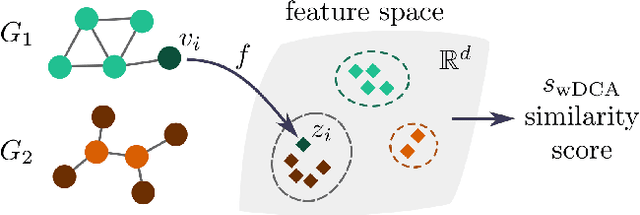
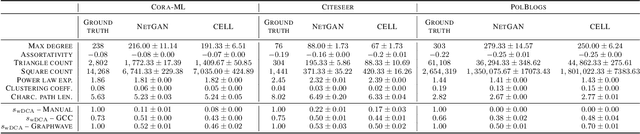
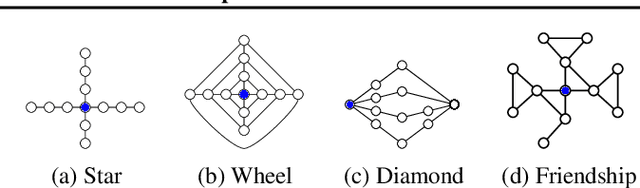
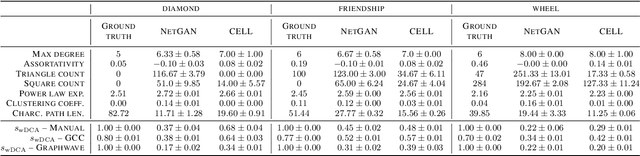
We argue that when comparing two graphs, the distribution of node structural features is more informative than global graph statistics which are often used in practice, especially to evaluate graph generative models. Thus, we present GraphDCA - a framework for evaluating similarity between graphs based on the alignment of their respective node representation sets. The sets are compared using a recently proposed method for comparing representation spaces, called Delaunay Component Analysis (DCA), which we extend to graph data. To evaluate our framework, we generate a benchmark dataset of graphs exhibiting different structural patterns and show, using three node structure feature extractors, that GraphDCA recognizes graphs with both similar and dissimilar local structure. We then apply our framework to evaluate three publicly available real-world graph datasets and demonstrate, using gradual edge perturbations, that GraphDCA satisfyingly captures gradually decreasing similarity, unlike global statistics. Finally, we use GraphDCA to evaluate two state-of-the-art graph generative models, NetGAN and CELL, and conclude that further improvements are needed for these models to adequately reproduce local structural features.

Comparing Reconstruction- and Contrastive-based Models for Visual Task Planning

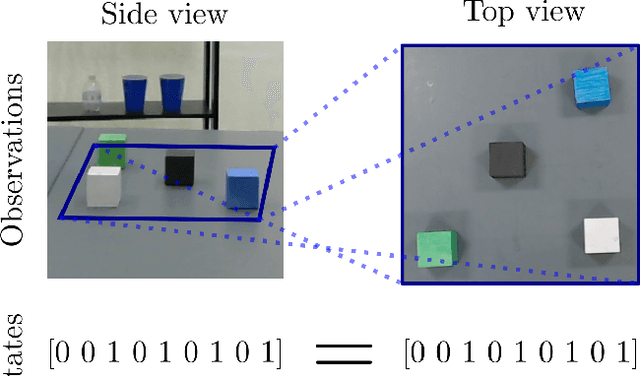
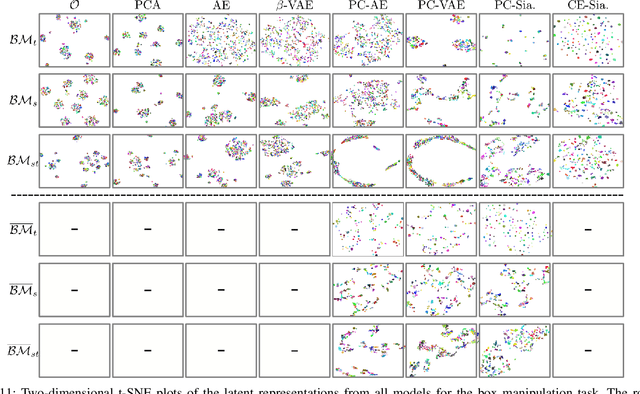
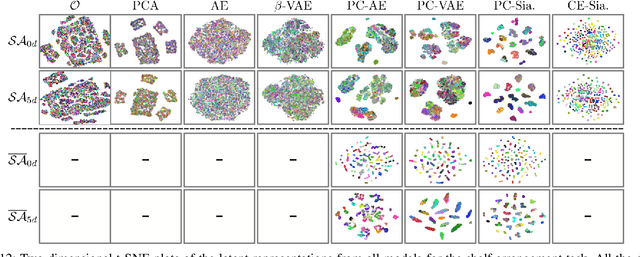
Learning state representations enables robotic planning directly from raw observations such as images. Most methods learn state representations by utilizing losses based on the reconstruction of the raw observations from a lower-dimensional latent space. The similarity between observations in the space of images is often assumed and used as a proxy for estimating similarity between the underlying states of the system. However, observations commonly contain task-irrelevant factors of variation which are nonetheless important for reconstruction, such as varying lighting and different camera viewpoints. In this work, we define relevant evaluation metrics and perform a thorough study of different loss functions for state representation learning. We show that models exploiting task priors, such as Siamese networks with a simple contrastive loss, outperform reconstruction-based representations in visual task planning.

GeomCA: Geometric Evaluation of Data Representations

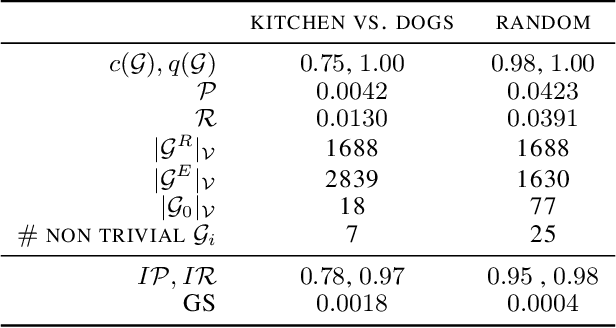
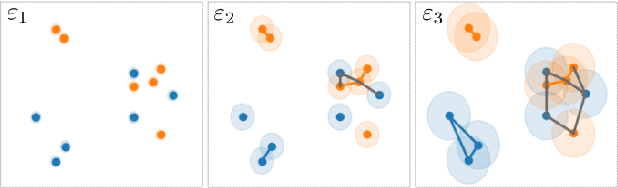
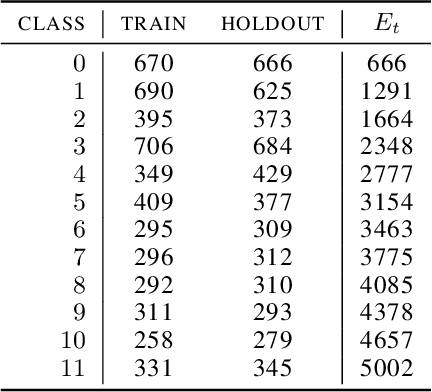
Evaluating the quality of learned representations without relying on a downstream task remains one of the challenges in representation learning. In this work, we present Geometric Component Analysis (GeomCA) algorithm that evaluates representation spaces based on their geometric and topological properties. GeomCA can be applied to representations of any dimension, independently of the model that generated them. We demonstrate its applicability by analyzing representations obtained from a variety of scenarios, such as contrastive learning models, generative models and supervised learning models.