Sample what you cant compress

For learned image representations, basic autoencoders often produce blurry results. Reconstruction quality can be improved by incorporating additional penalties such as adversarial (GAN) and perceptual losses. Arguably, these approaches lack a principled interpretation. Concurrently, in generative settings diffusion has demonstrated a remarkable ability to create crisp, high quality results and has solid theoretical underpinnings (from variational inference to direct study as the Fisher Divergence). Our work combines autoencoder representation learning with diffusion and is, to our knowledge, the first to demonstrate the efficacy of jointly learning a continuous encoder and decoder under a diffusion-based loss. We demonstrate that this approach yields better reconstruction quality as compared to GAN-based autoencoders while being easier to tune. We also show that the resulting representation is easier to model with a latent diffusion model as compared to the representation obtained from a state-of-the-art GAN-based loss. Since our decoder is stochastic, it can generate details not encoded in the otherwise deterministic latent representation; we therefore name our approach "Sample what you can't compress", or SWYCC for short.

Federated Variational Inference: Towards Improved Personalization and Generalization

Conventional federated learning algorithms train a single global model by leveraging all participating clients' data. However, due to heterogeneity in client generative distributions and predictive models, these approaches may not appropriately approximate the predictive process, converge to an optimal state, or generalize to new clients. We study personalization and generalization in stateless cross-device federated learning setups assuming heterogeneity in client data distributions and predictive models. We first propose a hierarchical generative model and formalize it using Bayesian Inference. We then approximate this process using Variational Inference to train our model efficiently. We call this algorithm Federated Variational Inference (FedVI). We use PAC-Bayes analysis to provide generalization bounds for FedVI. We evaluate our model on FEMNIST and CIFAR-100 image classification and show that FedVI beats the state-of-the-art on both tasks.

Automatically Bounding the Taylor Remainder Series: Tighter Bounds and New Applications

We present a new algorithm for automatically bounding the Taylor remainder series. In the special case of a scalar function $f: \mathbb{R} \mapsto \mathbb{R}$, our algorithm takes as input a reference point $x_0$, trust region $[a, b]$, and integer $k \ge 0$, and returns an interval $I$ such that $f(x) - \sum_{i=0}^k \frac {f^{(i)}(x_0)} {i!} (x - x_0)^i \in I (x - x_0)^{k+1}$ for all $x \in [a, b]$. As in automatic differentiation, the function $f$ is provided to the algorithm in symbolic form, and must be composed of known elementary functions. At a high level, our algorithm has two steps. First, for a variety of commonly-used elementary functions (e.g., $\exp$, $\log$), we derive sharp polynomial upper and lower bounds on the Taylor remainder series. We then recursively combine the bounds for the elementary functions using an interval arithmetic variant of Taylor-mode automatic differentiation. Our algorithm can make efficient use of machine learning hardware accelerators, and we provide an open source implementation in JAX. We then turn our attention to applications. Most notably, we use our new machinery to create the first universal majorization-minimization optimization algorithms: algorithms that iteratively minimize an arbitrary loss using a majorizer that is derived automatically, rather than by hand. Applied to machine learning, this leads to architecture-specific optimizers for training deep networks that converge from any starting point, without hyperparameter tuning. Our experiments show that for some optimization problems, these hyperparameter-free optimizers outperform tuned versions of gradient descent, Adam, and AdaGrad. We also show that our automatically-derived bounds can be used for verified global optimization and numerical integration, and to prove sharper versions of Jensen's inequality.

Weighted Ensemble Self-Supervised Learning

Ensembling has proven to be a powerful technique for boosting model performance, uncertainty estimation, and robustness in supervised learning. Advances in self-supervised learning (SSL) enable leveraging large unlabeled corpora for state-of-the-art few-shot and supervised learning performance. In this paper, we explore how ensemble methods can improve recent SSL techniques by developing a framework that permits data-dependent weighted cross-entropy losses. We refrain from ensembling the representation backbone; this choice yields an efficient ensemble method that incurs a small training cost and requires no architectural changes or computational overhead to downstream evaluation. The effectiveness of our method is demonstrated with two state-of-the-art SSL methods, DINO (Caron et al., 2021) and MSN (Assran et al., 2022). Our method outperforms both in multiple evaluation metrics on ImageNet-1K, particularly in the few-shot setting. We explore several weighting schemes and find that those which increase the diversity of ensemble heads lead to better downstream evaluation results. Thorough experiments yield improved prior art baselines which our method still surpasses; e.g., our overall improvement with MSN ViT-B/16 is 3.9 p.p. for 1-shot learning.

PAC$^m$-Bayes: Narrowing the Empirical Risk Gap in the Misspecified Bayesian Regime

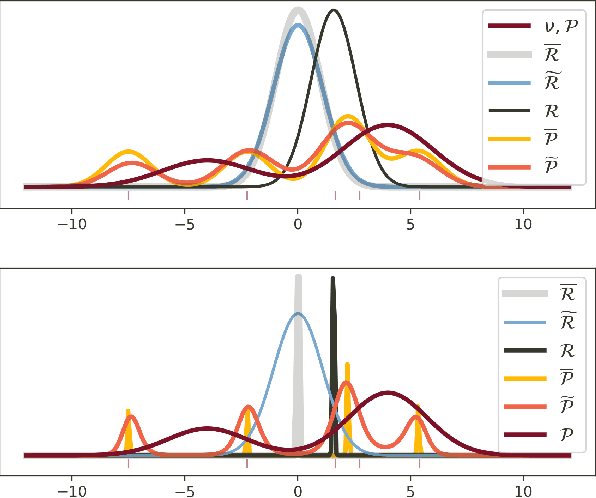
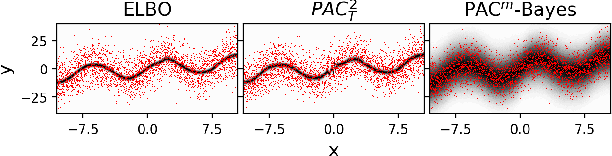
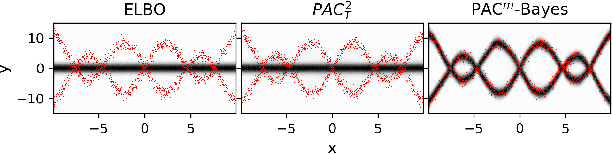
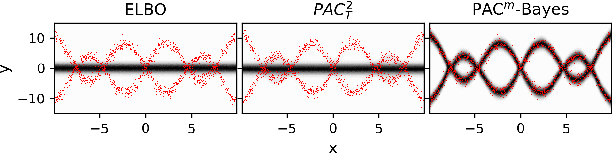
While the decision-theoretic optimality of the Bayesian formalism under correct model specification is well-known (Berger 2013), the Bayesian case becomes less clear under model misspecification (Grunwald 2017; Ramamoorthi 2015; Fushiki 2005). To formally understand the consequences of Bayesian misspecification, this work examines the relationship between posterior predictive risk and its sensitivity to correct model assumptions, i.e., choice of likelihood and prior. We present the multisample PAC$^m$-Bayes risk. This risk is justified by theoretical analysis based on PAC-Bayes as well as empirical study on a number of toy problems. The PAC$^m$-Bayes risk is appealing in that it entails direct minimization of the Monte-Carlo approximated posterior predictive risk yet recovers both the Bayesian formalism as well as the MLE in its limits. Our work is heavily influenced by Masegosa (2019); our contributions are to align training and generalization risks while offering a tighter bound which empirically performs at least as well and sometimes much better.

Density of States Estimation for Out-of-Distribution Detection

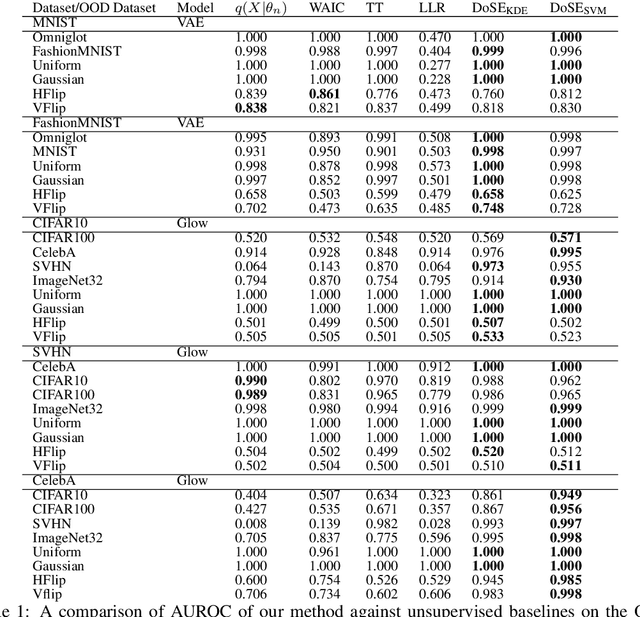
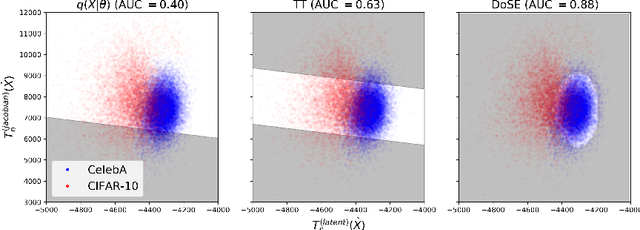
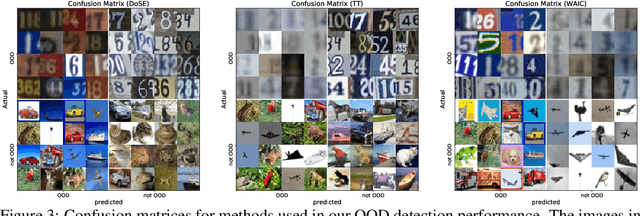
Perhaps surprisingly, recent studies have shown probabilistic model likelihoods have poor specificity for out-of-distribution (OOD) detection and often assign higher likelihoods to OOD data than in-distribution data. To ameliorate this issue we propose DoSE, the density of states estimator. Drawing on the statistical physics notion of ``density of states,'' the DoSE decision rule avoids direct comparison of model probabilities, and instead utilizes the ``probability of the model probability,'' or indeed the frequency of any reasonable statistic. The frequency is calculated using nonparametric density estimators (e.g., KDE and one-class SVM) which measure the typicality of various model statistics given the training data and from which we can flag test points with low typicality as anomalous. Unlike many other methods, DoSE requires neither labeled data nor OOD examples. DoSE is modular and can be trivially applied to any existing, trained model. We demonstrate DoSE's state-of-the-art performance against other unsupervised OOD detectors on previously established ``hard'' benchmarks.

Automatic Differentiation Variational Inference with Mixtures

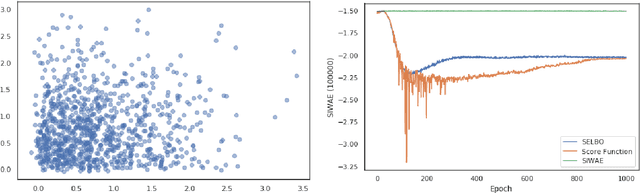
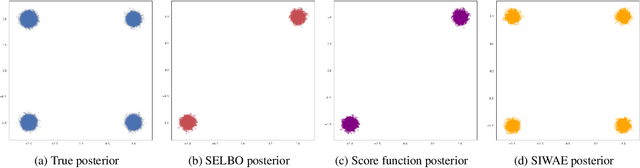
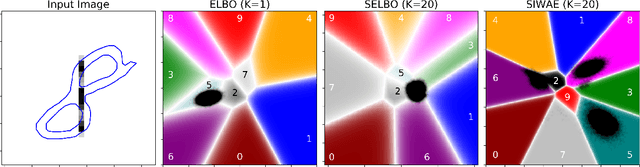
Automatic Differentiation Variational Inference (ADVI) is a useful tool for efficiently learning probabilistic models in machine learning. Generally approximate posteriors learned by ADVI are forced to be unimodal in order to facilitate use of the reparameterization trick. In this paper, we show how stratified sampling may be used to enable mixture distributions as the approximate posterior, and derive a new lower bound on the evidence analogous to the importance weighted autoencoder (IWAE). We show that this "SIWAE" is a tighter bound than both IWAE and the traditional ELBO, both of which are special instances of this bound. We verify empirically that the traditional ELBO objective disfavors the presence of multimodal posterior distributions and may therefore not be able to fully capture structure in the latent space. Our experiments show that using the SIWAE objective allows the encoder to learn more complex distributions which regularly contain multimodality, resulting in higher accuracy and better calibration in the presence of incomplete, limited, or corrupted data.

The k-tied Normal Distribution: A Compact Parameterization of Gaussian Mean Field Posteriors in Bayesian Neural Networks

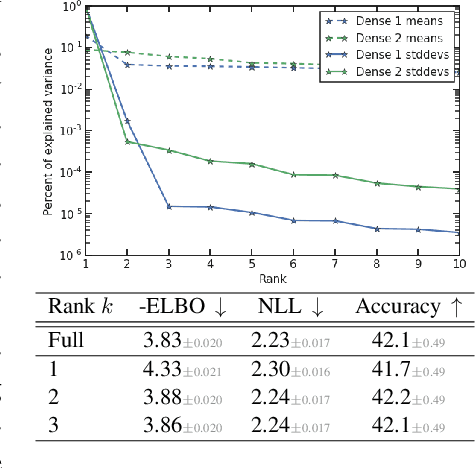
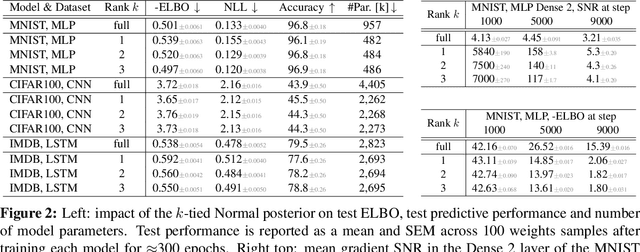
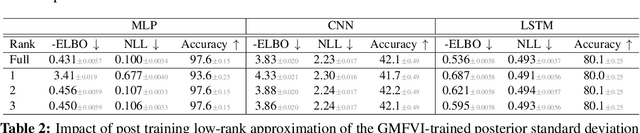
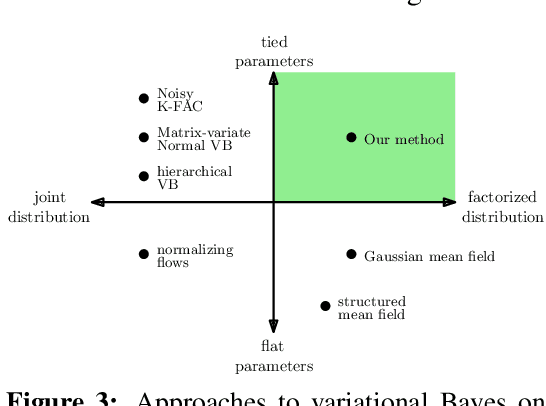
Variational Bayesian Inference is a popular methodology for approximating posterior distributions over Bayesian neural network weights. Recent work developing this class of methods has explored ever richer parameterizations of the approximate posterior in the hope of improving performance. In contrast, here we share a curious experimental finding that suggests instead restricting the variational distribution to a more compact parameterization. For a variety of deep Bayesian neural networks trained using Gaussian mean-field variational inference, we find that the posterior standard deviations consistently exhibit strong low-rank structure after convergence. This means that by decomposing these variational parameters into a low-rank factorization, we can make our variational approximation more compact without decreasing the models' performance. Furthermore, we find that such factorized parameterizations improve the signal-to-noise ratio of stochastic gradient estimates of the variational lower bound, resulting in faster convergence.

tfp.mcmc: Modern Markov Chain Monte Carlo Tools Built for Modern Hardware

Markov chain Monte Carlo (MCMC) is widely regarded as one of the most important algorithms of the 20th century. Its guarantees of asymptotic convergence, stability, and estimator-variance bounds using only unnormalized probability functions make it indispensable to probabilistic programming. In this paper, we introduce the TensorFlow Probability MCMC toolkit, and discuss some of the considerations that motivated its design.

Joint Distributions for TensorFlow Probability

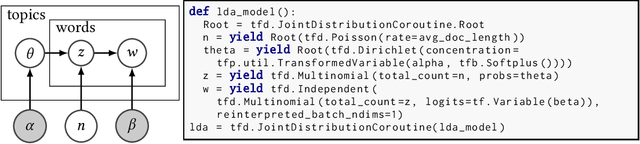
A central tenet of probabilistic programming is that a model is specified exactly once in a canonical representation which is usable by inference algorithms. We describe JointDistributions, a family of declarative representations of directed graphical models in TensorFlow Probability.