On Evaluating Loss Functions for Stock Ranking: An Empirical Analysis With Transformer Model

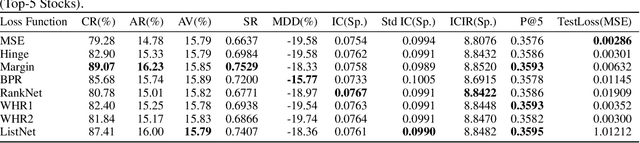
Quantitative trading strategies rely on accurately ranking stocks to identify profitable investments. Effective portfolio management requires models that can reliably order future stock returns. Transformer models are promising for understanding financial time series, but how different training loss functions affect their ability to rank stocks well is not yet fully understood. Financial markets are challenging due to their changing nature and complex relationships between stocks. Standard loss functions, which aim for simple prediction accuracy, often aren't enough. They don't directly teach models to learn the correct order of stock returns. While many advanced ranking losses exist from fields such as information retrieval, there hasn't been a thorough comparison to see how well they work for ranking financial returns, especially when used with modern Transformer models for stock selection. This paper addresses this gap by systematically evaluating a diverse set of advanced loss functions including pointwise, pairwise, listwise for daily stock return forecasting to facilitate rank-based portfolio selection on S&P 500 data. We focus on assessing how each loss function influences the model's ability to discern profitable relative orderings among assets. Our research contributes a comprehensive benchmark revealing how different loss functions impact a model's ability to learn cross-sectional and temporal patterns crucial for portfolio selection, thereby offering practical guidance for optimizing ranking-based trading strategies.

Moon: A Modality Conversion-based Efficient Multivariate Time Series Anomaly Detection

Multivariate time series (MTS) anomaly detection identifies abnormal patterns where each timestamp contains multiple variables. Existing MTS anomaly detection methods fall into three categories: reconstruction-based, prediction-based, and classifier-based methods. However, these methods face two key challenges: (1) Unsupervised learning methods, such as reconstruction-based and prediction-based methods, rely on error thresholds, which can lead to inaccuracies; (2) Semi-supervised methods mainly model normal data and often underuse anomaly labels, limiting detection of subtle anomalies;(3) Supervised learning methods, such as classifier-based approaches, often fail to capture local relationships, incur high computational costs, and are constrained by the scarcity of labeled data. To address these limitations, we propose Moon, a supervised modality conversion-based multivariate time series anomaly detection framework. Moon enhances the efficiency and accuracy of anomaly detection while providing detailed anomaly analysis reports. First, Moon introduces a novel multivariate Markov Transition Field (MV-MTF) technique to convert numeric time series data into image representations, capturing relationships across variables and timestamps. Since numeric data retains unique patterns that cannot be fully captured by image conversion alone, Moon employs a Multimodal-CNN to integrate numeric and image data through a feature fusion model with parameter sharing, enhancing training efficiency. Finally, a SHAP-based anomaly explainer identifies key variables contributing to anomalies, improving interpretability. Extensive experiments on six real-world MTS datasets demonstrate that Moon outperforms six state-of-the-art methods by up to 93% in efficiency, 4% in accuracy and, 10.8% in interpretation performance.

Titans Revisited: A Lightweight Reimplementation and Critical Analysis of a Test-Time Memory Model

By the end of 2024, Google researchers introduced Titans: Learning at Test Time, a neural memory model achieving strong empirical results across multiple tasks. However, the lack of publicly available code and ambiguities in the original description hinder reproducibility. In this work, we present a lightweight reimplementation of Titans and conduct a comprehensive evaluation on Masked Language Modeling, Time Series Forecasting, and Recommendation tasks. Our results reveal that Titans does not always outperform established baselines due to chunking. However, its Neural Memory component consistently improves performance compared to attention-only models. These findings confirm the model's innovative potential while highlighting its practical limitations and raising questions for future research.

Bayesian Nonparametric Dynamical Clustering of Time Series

We present a method that models the evolution of an unbounded number of time series clusters by switching among an unknown number of regimes with linear dynamics. We develop a Bayesian non-parametric approach using a hierarchical Dirichlet process as a prior on the parameters of a Switching Linear Dynamical System and a Gaussian process prior to model the statistical variations in amplitude and temporal alignment within each cluster. By modeling the evolution of time series patterns, the method avoids unnecessary proliferation of clusters in a principled manner. We perform inference by formulating a variational lower bound for off-line and on-line scenarios, enabling efficient learning through optimization. We illustrate the versatility and effectiveness of the approach through several case studies of electrocardiogram analysis using publicly available databases.

TimeEmb: A Lightweight Static-Dynamic Disentanglement Framework for Time Series Forecasting

Temporal non-stationarity, the phenomenon that time series distributions change over time, poses fundamental challenges to reliable time series forecasting. Intuitively, the complex time series can be decomposed into two factors, \ie time-invariant and time-varying components, which indicate static and dynamic patterns, respectively. Nonetheless, existing methods often conflate the time-varying and time-invariant components, and jointly learn the combined long-term patterns and short-term fluctuations, leading to suboptimal performance facing distribution shifts. To address this issue, we initiatively propose a lightweight static-dynamic decomposition framework, TimeEmb, for time series forecasting. TimeEmb innovatively separates time series into two complementary components: (1) time-invariant component, captured by a novel global embedding module that learns persistent representations across time series, and (2) time-varying component, processed by an efficient frequency-domain filtering mechanism inspired by full-spectrum analysis in signal processing. Experiments on real-world datasets demonstrate that TimeEmb outperforms state-of-the-art baselines and requires fewer computational resources. We conduct comprehensive quantitative and qualitative analyses to verify the efficacy of static-dynamic disentanglement. This lightweight framework can also improve existing time-series forecasting methods with simple integration. To ease reproducibility, the code is available at https://github.com/showmeon/TimeEmb.

Topology of Currencies: Persistent Homology for FX Co-movements: A Comparative Clustering Study

This study investigates whether Topological Data Analysis (TDA) can provide additional insights beyond traditional statistical methods in clustering currency behaviours. We focus on the foreign exchange (FX) market, which is a complex system often exhibiting non-linear and high-dimensional dynamics that classical techniques may not fully capture. We compare clustering results based on TDA-derived features versus classical statistical features using monthly logarithmic returns of 13 major currency exchange rates (all against the euro). Two widely-used clustering algorithms, \(k\)-means and Hierarchical clustering, are applied on both types of features, and cluster quality is evaluated via the Silhouette score and the Calinski-Harabasz index. Our findings show that TDA-based feature clustering produces more compact and well-separated clusters than clustering on traditional statistical features, particularly achieving substantially higher Calinski-Harabasz scores. However, all clustering approaches yield modest Silhouette scores, underscoring the inherent difficulty of grouping FX time series. The differing cluster compositions under TDA vs. classical features suggest that TDA captures structural patterns in currency co-movements that conventional methods might overlook. These results highlight TDA as a valuable complementary tool for analysing financial time series, with potential applications in risk management where understanding structural co-movements is crucial.

Forecasting-Based Biomedical Time-series Data Synthesis for Open Data and Robust AI

The limited data availability due to strict privacy regulations and significant resource demands severely constrains biomedical time-series AI development, which creates a critical gap between data requirements and accessibility. Synthetic data generation presents a promising solution by producing artificial datasets that maintain the statistical properties of real biomedical time-series data without compromising patient confidentiality. We propose a framework for synthetic biomedical time-series data generation based on advanced forecasting models that accurately replicates complex electrophysiological signals such as EEG and EMG with high fidelity. These synthetic datasets preserve essential temporal and spectral properties of real data, which enables robust analysis while effectively addressing data scarcity and privacy challenges. Our evaluations across multiple subjects demonstrate that the generated synthetic data can serve as an effective substitute for real data and also significantly boost AI model performance. The approach maintains critical biomedical features while provides high scalability for various applications and integrates seamlessly into open-source repositories, substantially expanding resources for AI-driven biomedical research.

Benchmarking M-LTSF: Frequency and Noise-Based Evaluation of Multivariate Long Time Series Forecasting Models

Understanding the robustness of deep learning models for multivariate long-term time series forecasting (M-LTSF) remains challenging, as evaluations typically rely on real-world datasets with unknown noise properties. We propose a simulation-based evaluation framework that generates parameterizable synthetic datasets, where each dataset instance corresponds to a different configuration of signal components, noise types, signal-to-noise ratios, and frequency characteristics. These configurable components aim to model real-world multivariate time series data without the ambiguity of unknown noise. This framework enables fine-grained, systematic evaluation of M-LTSF models under controlled and diverse scenarios. We benchmark four representative architectures S-Mamba (state-space), iTransformer (transformer-based), R-Linear (linear), and Autoformer (decomposition-based). Our analysis reveals that all models degrade severely when lookback windows cannot capture complete periods of seasonal patters in the data. S-Mamba and Autoformer perform best on sawtooth patterns, while R-Linear and iTransformer favor sinusoidal signals. White and Brownian noise universally degrade performance with lower signal-to-noise ratio while S-Mamba shows specific trend-noise and iTransformer shows seasonal-noise vulnerability. Further spectral analysis shows that S-Mamba and iTransformer achieve superior frequency reconstruction. This controlled approach, based on our synthetic and principle-driven testbed, offers deeper insights into model-specific strengths and limitations through the aggregation of MSE scores and provides concrete guidance for model selection based on signal characteristics and noise conditions.

Deep learning motion correction of quantitative stress perfusion cardiovascular magnetic resonance

Background: Quantitative stress perfusion cardiovascular magnetic resonance (CMR) is a powerful tool for assessing myocardial ischemia. Motion correction is essential for accurate pixel-wise mapping but traditional registration-based methods are slow and sensitive to acquisition variability, limiting robustness and scalability. Methods: We developed an unsupervised deep learning-based motion correction pipeline that replaces iterative registration with efficient one-shot estimation. The method corrects motion in three steps and uses robust principal component analysis to reduce contrast-related effects. It aligns the perfusion series and auxiliary images (arterial input function and proton density-weighted series). Models were trained and validated on multivendor data from 201 patients, with 38 held out for testing. Performance was assessed via temporal alignment and quantitative perfusion values, compared to a previously published registration-based method. Results: The deep learning approach significantly improved temporal smoothness of time-intensity curves (p<0.001). Myocardial alignment (Dice = 0.92 (0.04) and 0.91 (0.05)) was comparable to the baseline and superior to before registration (Dice = 0.80 (0.09), p<0.001). Perfusion maps showed reduced motion, with lower standard deviation in the myocardium (0.52 (0.39) ml/min/g) compared to baseline (0.55 (0.44) ml/min/g). Processing time was reduced 15-fold. Conclusion: This deep learning pipeline enables fast, robust motion correction for stress perfusion CMR, improving accuracy across dynamic and auxiliary images. Trained on multivendor data, it generalizes across sequences and may facilitate broader clinical adoption of quantitative perfusion imaging.

VarCoNet: A variability-aware self-supervised framework for functional connectome extraction from resting-state fMRI

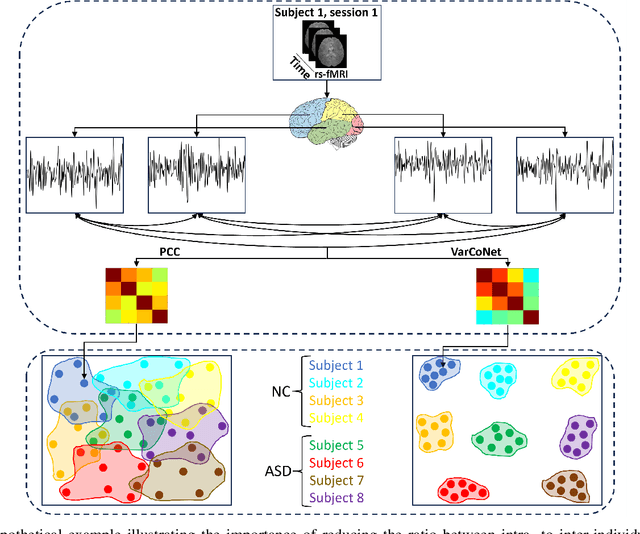
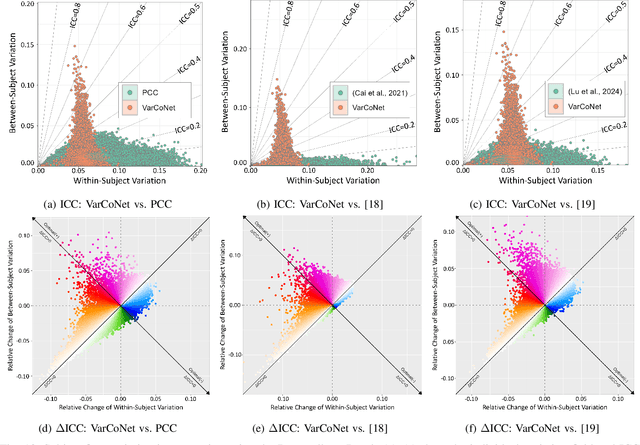
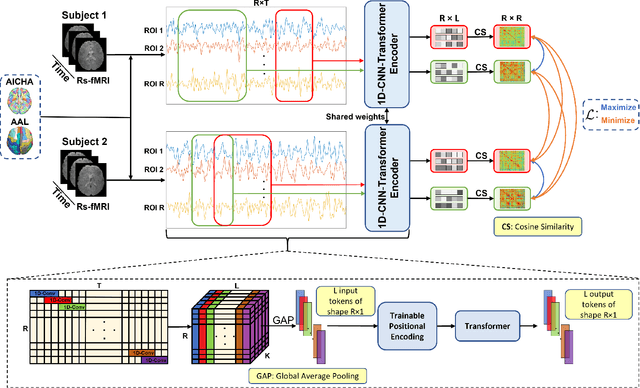
Accounting for inter-individual variability in brain function is key to precision medicine. Here, by considering functional inter-individual variability as meaningful data rather than noise, we introduce VarCoNet, an enhanced self-supervised framework for robust functional connectome (FC) extraction from resting-state fMRI (rs-fMRI) data. VarCoNet employs self-supervised contrastive learning to exploit inherent functional inter-individual variability, serving as a brain function encoder that generates FC embeddings readily applicable to downstream tasks even in the absence of labeled data. Contrastive learning is facilitated by a novel augmentation strategy based on segmenting rs-fMRI signals. At its core, VarCoNet integrates a 1D-CNN-Transformer encoder for advanced time-series processing, enhanced with a robust Bayesian hyperparameter optimization. Our VarCoNet framework is evaluated on two downstream tasks: (i) subject fingerprinting, using rs-fMRI data from the Human Connectome Project, and (ii) autism spectrum disorder (ASD) classification, using rs-fMRI data from the ABIDE I and ABIDE II datasets. Using different brain parcellations, our extensive testing against state-of-the-art methods, including 13 deep learning methods, demonstrates VarCoNet's superiority, robustness, interpretability, and generalizability. Overall, VarCoNet provides a versatile and robust framework for FC analysis in rs-fMRI.