Lintao Ye
Model-Free Output Feedback Stabilization via Policy Gradient Methods
Jan 29, 2026Abstract:Stabilizing a dynamical system is a fundamental problem that serves as a cornerstone for many complex tasks in the field of control systems. The problem becomes challenging when the system model is unknown. Among the Reinforcement Learning (RL) algorithms that have been successfully applied to solve problems pertaining to unknown linear dynamical systems, the policy gradient (PG) method stands out due to its ease of implementation and can solve the problem in a model-free manner. However, most of the existing works on PG methods for unknown linear dynamical systems assume full-state feedback. In this paper, we take a step towards model-free learning for partially observable linear dynamical systems with output feedback and focus on the fundamental stabilization problem of the system. We propose an algorithmic framework that stretches the boundary of PG methods to the problem without global convergence guarantees. We show that by leveraging zeroth-order PG update based on system trajectories and its convergence to stationary points, the proposed algorithms return a stabilizing output feedback policy for discrete-time linear dynamical systems. We also explicitly characterize the sample complexity of our algorithm and verify the effectiveness of the algorithm using numerical examples.
Output Feedback Stabilization of Linear Systems via Policy Gradient Methods
Jan 27, 2026Abstract:Stabilizing a dynamical system is a fundamental problem that serves as a cornerstone for many complex tasks in the field of control systems. The problem becomes challenging when the system model is unknown. Among the Reinforcement Learning (RL) algorithms that have been successfully applied to solve problems pertaining to unknown linear dynamical systems, the policy gradient (PG) method stands out due to its ease of implementation and can solve the problem in a model-free manner. However, most of the existing works on PG methods for unknown linear dynamical systems assume full-state feedback. In this paper, we take a step towards model-free learning for partially observable linear dynamical systems with output feedback and focus on the fundamental stabilization problem of the system. We propose an algorithmic framework that stretches the boundary of PG methods to the problem without global convergence guarantees. We show that by leveraging zeroth-order PG update based on system trajectories and its convergence to stationary points, the proposed algorithms return a stabilizing output feedback policy for discrete-time linear dynamical systems. We also explicitly characterize the sample complexity of our algorithm and verify the effectiveness of the algorithm using numerical examples.
Learning Stabilizing Policies via an Unstable Subspace Representation
May 02, 2025Abstract:We study the problem of learning to stabilize (LTS) a linear time-invariant (LTI) system. Policy gradient (PG) methods for control assume access to an initial stabilizing policy. However, designing such a policy for an unknown system is one of the most fundamental problems in control, and it may be as hard as learning the optimal policy itself. Existing work on the LTS problem requires large data as it scales quadratically with the ambient dimension. We propose a two-phase approach that first learns the left unstable subspace of the system and then solves a series of discounted linear quadratic regulator (LQR) problems on the learned unstable subspace, targeting to stabilize only the system's unstable dynamics and reduce the effective dimension of the control space. We provide non-asymptotic guarantees for both phases and demonstrate that operating on the unstable subspace reduces sample complexity. In particular, when the number of unstable modes is much smaller than the state dimension, our analysis reveals that LTS on the unstable subspace substantially speeds up the stabilization process. Numerical experiments are provided to support this sample complexity reduction achieved by our approach.
Online Convex Optimization with Memory and Limited Predictions
Oct 31, 2024

Abstract:We study the problem of online convex optimization with memory and predictions over a horizon $T$. At each time step, a decision maker is given some limited predictions of the cost functions from a finite window of future time steps, i.e., values of the cost function at certain decision points in the future. The decision maker then chooses an action and incurs a cost given by a convex function that depends on the actions chosen in the past. We propose an algorithm to solve this problem and show that the dynamic regret of the algorithm decays exponentially with the prediction window length. Our algorithm contains two general subroutines that work for wider classes of problems. The first subroutine can solve general online convex optimization with memory and bandit feedback with $\sqrt{T}$-dynamic regret with respect to $T$. The second subroutine is a zeroth-order method that can be used to solve general convex optimization problems with a linear convergence rate that matches the best achievable rate of first-order methods for convex optimization. The key to our algorithm design and analysis is the use of truncated Gaussian smoothing when querying the decision points for obtaining the predictions. We complement our theoretical results using numerical experiments.
Submodular Maximization Approaches for Equitable Client Selection in Federated Learning
Aug 24, 2024Abstract:In a conventional Federated Learning framework, client selection for training typically involves the random sampling of a subset of clients in each iteration. However, this random selection often leads to disparate performance among clients, raising concerns regarding fairness, particularly in applications where equitable outcomes are crucial, such as in medical or financial machine learning tasks. This disparity typically becomes more pronounced with the advent of performance-centric client sampling techniques. This paper introduces two novel methods, namely SUBTRUNC and UNIONFL, designed to address the limitations of random client selection. Both approaches utilize submodular function maximization to achieve more balanced models. By modifying the facility location problem, they aim to mitigate the fairness concerns associated with random selection. SUBTRUNC leverages client loss information to diversify solutions, while UNIONFL relies on historical client selection data to ensure a more equitable performance of the final model. Moreover, these algorithms are accompanied by robust theoretical guarantees regarding convergence under reasonable assumptions. The efficacy of these methods is demonstrated through extensive evaluations across heterogeneous scenarios, revealing significant improvements in fairness as measured by a client dissimilarity metric.
Towards Model-Free LQR Control over Rate-Limited Channels
Jan 02, 2024Abstract:Given the success of model-free methods for control design in many problem settings, it is natural to ask how things will change if realistic communication channels are utilized for the transmission of gradients or policies. While the resulting problem has analogies with the formulations studied under the rubric of networked control systems, the rich literature in that area has typically assumed that the model of the system is known. As a step towards bridging the fields of model-free control design and networked control systems, we ask: \textit{Is it possible to solve basic control problems - such as the linear quadratic regulator (LQR) problem - in a model-free manner over a rate-limited channel?} Toward answering this question, we study a setting where a worker agent transmits quantized policy gradients (of the LQR cost) to a server over a noiseless channel with a finite bit-rate. We propose a new algorithm titled Adaptively Quantized Gradient Descent (\texttt{AQGD}), and prove that above a certain finite threshold bit-rate, \texttt{AQGD} guarantees exponentially fast convergence to the globally optimal policy, with \textit{no deterioration of the exponent relative to the unquantized setting}. More generally, our approach reveals the benefits of adaptive quantization in preserving fast linear convergence rates, and, as such, may be of independent interest to the literature on compressed optimization.
Learning Dynamical Systems by Leveraging Data from Similar Systems
Feb 08, 2023



Abstract:We consider the problem of learning the dynamics of a linear system when one has access to data generated by an auxiliary system that shares similar (but not identical) dynamics, in addition to data from the true system. We use a weighted least squares approach, and provide a finite sample error bound of the learned model as a function of the number of samples and various system parameters from the two systems as well as the weight assigned to the auxiliary data. We show that the auxiliary data can help to reduce the intrinsic system identification error due to noise, at the price of adding a portion of error that is due to the differences between the two system models. We further provide a data-dependent bound that is computable when some prior knowledge about the systems is available. This bound can also be used to determine the weight that should be assigned to the auxiliary data during the model training stage.
Regret Bounds for Learning Decentralized Linear Quadratic Regulator with Partially Nested Information Structure
Oct 17, 2022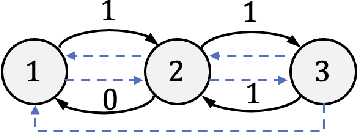
Abstract:We study the problem of learning decentralized linear quadratic regulator under a partially nested information constraint, when the system model is unknown a priori. We propose an online learning algorithm that adaptively designs a control policy as new data samples from a single system trajectory become available. Our algorithm design uses a disturbance-feedback representation of state-feedback controllers coupled with online convex optimization with memory and delayed feedback. We show that our online algorithm yields a controller that satisfies the desired information constraint and enjoys an expected regret that scales as $\sqrt{T}$ with the time horizon $T$.
Identifying the Dynamics of a System by Leveraging Data from Similar Systems
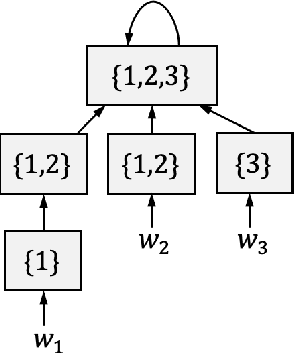
Apr 11, 2022
Abstract:We study the problem of identifying the dynamics of a linear system when one has access to samples generated by a similar (but not identical) system, in addition to data from the true system. We use a weighted least squares approach and provide finite sample performance guarantees on the quality of the identified dynamics. Our results show that one can effectively use the auxiliary data generated by the similar system to reduce the estimation error due to the process noise, at the cost of adding a portion of error that is due to intrinsic differences in the models of the true and auxiliary systems. We also provide numerical experiments to validate our theoretical results. Our analysis can be applied to a variety of important settings. For example, if the system dynamics change at some point in time (e.g., due to a fault), how should one leverage data from the prior system in order to learn the dynamics of the new system? As another example, if there is abundant data available from a simulated (but imperfect) model of the true system, how should one weight that data compared to the real data from the system? Our analysis provides insights into the answers to these questions.
On the Sample Complexity of Decentralized Linear Quadratic Regulator with Partially Nested Information Structure
Oct 14, 2021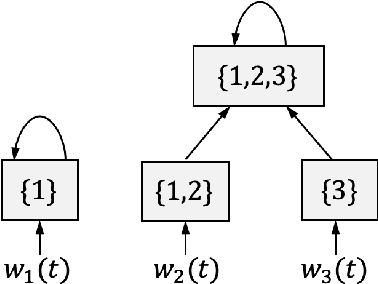
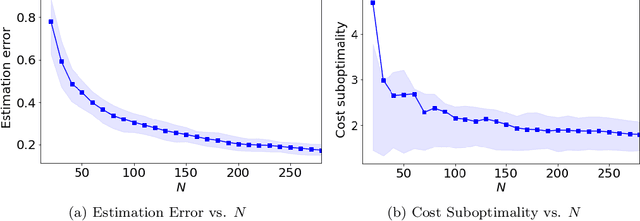
Abstract:We study the problem of control policy design for decentralized state-feedback linear quadratic control with a partially nested information structure, when the system model is unknown. We propose a model-based learning solution, which consists of two steps. First, we estimate the unknown system model from a single system trajectory of finite length, using least squares estimation. Next, based on the estimated system model, we design a control policy that satisfies the desired information structure. We show that the suboptimality gap between our control policy and the optimal decentralized control policy (designed using accurate knowledge of the system model) scales linearly with the estimation error of the system model. Using this result, we provide an end-to-end sample complexity result for learning decentralized controllers for a linear quadratic control problem with a partially nested information structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge