The Nonlocal Neural Operator: Universal Approximation

Neural operator architectures approximate operators between infinite-dimensional Banach spaces of functions. They are gaining increased attention in computational science and engineering, due to their potential both to accelerate traditional numerical methods and to enable data-driven discovery. A popular variant of neural operators is the Fourier neural operator (FNO). Previous analysis proving universal operator approximation theorems for FNOs resorts to use of an unbounded number of Fourier modes and limits the basic form of the method to problems with periodic geometry. Prior work relies on intuition from traditional numerical methods, and interprets the FNO as a nonstandard and highly nonlinear spectral method. The present work challenges this point of view in two ways: (i) the work introduces a new broad class of operator approximators, termed nonlocal neural operators (NNOs), which allow for operator approximation between functions defined on arbitrary geometries, and includes the FNO as a special case; and (ii) analysis of the NNOs shows that, provided this architecture includes computation of a spatial average (corresponding to retaining only a single Fourier mode in the special case of the FNO) it benefits from universal approximation. It is demonstrated that this theoretical result unifies the analysis of a wide range of neural operator architectures. Furthermore, it sheds new light on the role of nonlocality, and its interaction with nonlinearity, thereby paving the way for a more systematic exploration of nonlocality, both through the development of new operator learning architectures and the analysis of existing and new architectures.

Forecasting subcritical cylinder wakes with Fourier Neural Operators

We apply Fourier neural operators (FNOs), a state-of-the-art operator learning technique, to forecast the temporal evolution of experimentally measured velocity fields. FNOs are a recently developed machine learning method capable of approximating solution operators to systems of partial differential equations through data alone. The learned FNO solution operator can be evaluated in milliseconds, potentially enabling faster-than-real-time modeling for predictive flow control in physical systems. Here we use FNOs to predict how physical fluid flows evolve in time, training with particle image velocimetry measurements depicting cylinder wakes in the subcritical vortex shedding regime. We train separate FNOs at Reynolds numbers ranging from Re = 240 to Re = 3060 and study how increasingly turbulent flow phenomena impact prediction accuracy. We focus here on a short prediction horizon of ten non-dimensionalized time-steps, as would be relevant for problems of predictive flow control. We find that FNOs are capable of accurately predicting the evolution of experimental velocity fields throughout the range of Reynolds numbers tested (L2 norm error < 0.1) despite being provided with limited and imperfect flow observations. Given these results, we conclude that this method holds significant potential for real-time predictive flow control of physical systems.

Incremental Fourier Neural Operator

Recently, neural networks have proven their impressive ability to solve partial differential equations (PDEs). Among them, Fourier neural operator (FNO) has shown success in learning solution operators for highly non-linear problems such as turbulence flow. FNO is discretization-invariant, where it can be trained on low-resolution data and generalizes to problems with high-resolution. This property is related to the low-pass filters in FNO, where only a limited number of frequency modes are selected to propagate information. However, it is still a challenge to select an appropriate number of frequency modes and training resolution for different PDEs. Too few frequency modes and low-resolution data hurt generalization, while too many frequency modes and high-resolution data are computationally expensive and lead to over-fitting. To this end, we propose Incremental Fourier Neural Operator (IFNO), which augments both the frequency modes and data resolution incrementally during training. We show that IFNO achieves better generalization (around 15% reduction on testing L2 loss) while reducing the computational cost by 35%, compared to the standard FNO. In addition, we observe that IFNO follows the behavior of implicit regularization in FNO, which explains its excellent generalization ability.

Fourier Continuation for Exact Derivative Computation in Physics-Informed Neural Operators

The physics-informed neural operator (PINO) is a machine learning architecture that has shown promising empirical results for learning partial differential equations. PINO uses the Fourier neural operator (FNO) architecture to overcome the optimization challenges often faced by physics-informed neural networks. Since the convolution operator in PINO uses the Fourier series representation, its gradient can be computed exactly on the Fourier space. While Fourier series cannot represent nonperiodic functions, PINO and FNO still have the expressivity to learn nonperiodic problems with Fourier extension via padding. However, computing the Fourier extension in the physics-informed optimization requires solving an ill-conditioned system, resulting in inaccurate derivatives which prevent effective optimization. In this work, we present an architecture that leverages Fourier continuation (FC) to apply the exact gradient method to PINO for nonperiodic problems. This paper investigates three different ways that FC can be incorporated into PINO by testing their performance on a 1D blowup problem. Experiments show that FC-PINO outperforms padded PINO, improving equation loss by several orders of magnitude, and it can accurately capture the third order derivatives of nonsmooth solution functions.

Machine Learning Accelerated PDE Backstepping Observers

State estimation is important for a variety of tasks, from forecasting to substituting for unmeasured states in feedback controllers. Performing real-time state estimation for PDEs using provably and rapidly converging observers, such as those based on PDE backstepping, is computationally expensive and in many cases prohibitive. We propose a framework for accelerating PDE observer computations using learning-based approaches that are much faster while maintaining accuracy. In particular, we employ the recently-developed Fourier Neural Operator (FNO) to learn the functional mapping from the initial observer state and boundary measurements to the state estimate. By employing backstepping observer gains for previously-designed observers with particular convergence rate guarantees, we provide numerical experiments that evaluate the increased computational efficiency gained with FNO. We consider the state estimation for three benchmark PDE examples motivated by applications: first, for a reaction-diffusion (parabolic) PDE whose state is estimated with an exponential rate of convergence; second, for a parabolic PDE with exact prescribed-time estimation; and, third, for a pair of coupled first-order hyperbolic PDEs that modeling traffic flow density and velocity. The ML-accelerated observers trained on simulation data sets for these PDEs achieves up to three orders of magnitude improvement in computational speed compared to classical methods. This demonstrates the attractiveness of the ML-accelerated observers for real-time state estimation and control.

Accelerating Carbon Capture and Storage Modeling using Fourier Neural Operators

Carbon capture and storage (CCS) is an important strategy for reducing carbon dioxide emissions and mitigating climate change. We consider the storage aspect of CCS, which involves injecting carbon dioxide into underground reservoirs. This requires accurate and high-resolution predictions of carbon dioxide plume migration and reservoir pressure buildup. However, such modeling is challenging at scale due to the high computational costs of existing numerical methods. We introduce a novel machine learning approach for four-dimensional spatial-temporal modeling, which speeds up predictions nearly 700,000 times compared to existing methods. It provides highly accurate predictions under diverse reservoir conditions, geological heterogeneity, and injection schemes. Our framework, Nested Fourier Neural Operator (FNO), learns the solution operator for the family of partial differential equations governing the carbon dioxide-water multiphase flow. It uses a hierarchy of FNO models to produce outputs at different refinement levels. Thus, our approach enables unprecedented real-time high-resolution modeling for carbon dioxide storage.

Improving Transferability of Adversarial Examples on Face Recognition with Beneficial Perturbation Feature Augmentation

Face recognition (FR) models can be easily fooled by adversarial examples, which are crafted by adding imperceptible perturbations on benign face images. To improve the transferability of adversarial examples on FR models, we propose a novel attack method called Beneficial Perturbation Feature Augmentation Attack (BPFA), which reduces the overfitting of the adversarial examples to surrogate FR models by the adversarial strategy. Specifically, in the backpropagation step, BPFA records the gradients on pre-selected features and uses the gradient on the input image to craft adversarial perturbation to be added on the input image. In the next forward propagation step, BPFA leverages the recorded gradients to add perturbations(i.e., beneficial perturbations) that can be pitted against the adversarial perturbation added on the input image on their corresponding features. The above two steps are repeated until the last backpropagation step before the maximum number of iterations is reached. The optimization process of the adversarial perturbation added on the input image and the optimization process of the beneficial perturbations added on the features correspond to a minimax two-player game. Extensive experiments demonstrate that BPFA outperforms the state-of-the-art gradient-based adversarial attacks on FR.

An Adversarial Active Sampling-based Data Augmentation Framework for Manufacturable Chip Design

Lithography modeling is a crucial problem in chip design to ensure a chip design mask is manufacturable. It requires rigorous simulations of optical and chemical models that are computationally expensive. Recent developments in machine learning have provided alternative solutions in replacing the time-consuming lithography simulations with deep neural networks. However, the considerable accuracy drop still impedes its industrial adoption. Most importantly, the quality and quantity of the training dataset directly affect the model performance. To tackle this problem, we propose a litho-aware data augmentation (LADA) framework to resolve the dilemma of limited data and improve the machine learning model performance. First, we pretrain the neural networks for lithography modeling and a gradient-friendly StyleGAN2 generator. We then perform adversarial active sampling to generate informative and synthetic in-distribution mask designs. These synthetic mask images will augment the original limited training dataset used to finetune the lithography model for improved performance. Experimental results demonstrate that LADA can successfully exploits the neural network capacity by narrowing down the performance gap between the training and testing data instances.

Fourier Neural Operator with Learned Deformations for PDEs on General Geometries

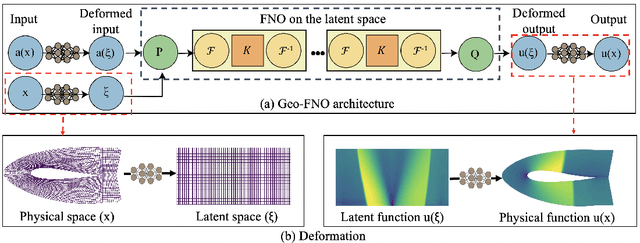
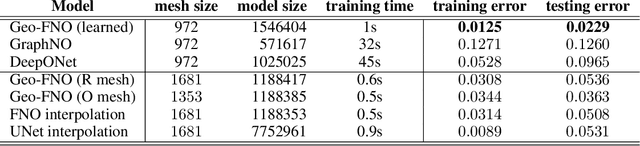
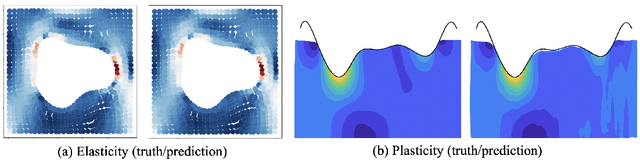
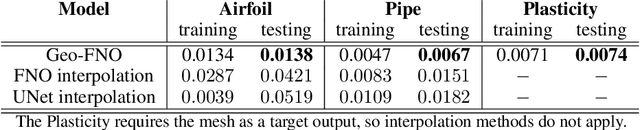
Deep learning surrogate models have shown promise in solving partial differential equations (PDEs). Among them, the Fourier neural operator (FNO) achieves good accuracy, and is significantly faster compared to numerical solvers, on a variety of PDEs, such as fluid flows. However, the FNO uses the Fast Fourier transform (FFT), which is limited to rectangular domains with uniform grids. In this work, we propose a new framework, viz., geo-FNO, to solve PDEs on arbitrary geometries. Geo-FNO learns to deform the input (physical) domain, which may be irregular, into a latent space with a uniform grid. The FNO model with the FFT is applied in the latent space. The resulting geo-FNO model has both the computation efficiency of FFT and the flexibility of handling arbitrary geometries. Our geo-FNO is also flexible in terms of its input formats, viz., point clouds, meshes, and design parameters are all valid inputs. We consider a variety of PDEs such as the Elasticity, Plasticity, Euler's, and Navier-Stokes equations, and both forward modeling and inverse design problems. Geo-FNO is $10^5$ times faster than the standard numerical solvers and twice more accurate compared to direct interpolation on existing ML-based PDE solvers such as the standard FNO.

Large Scale Mask Optimization Via Convolutional Fourier Neural Operator and Litho-Guided Self Training

Machine learning techniques have been extensively studied for mask optimization problems, aiming at better mask printability, shorter turnaround time, better mask manufacturability, and so on. However, most of these researches are focusing on the initial solution generation of small design regions. To further realize the potential of machine learning techniques on mask optimization tasks, we present a Convolutional Fourier Neural Operator (CFNO) that can efficiently learn layout tile dependencies and hence promise stitch-less large-scale mask optimization with the limited intervention of legacy tools. We discover the possibility of litho-guided self-training (LGST) through a trained machine learning model when solving non-convex optimization problems, which allows iterative model and dataset update and brings significant model performance improvement. Experimental results show that, for the first time, our machine learning-based framework outperforms state-of-the-art academic numerical mask optimizers with an order of magnitude speedup.