Nonlinear spiked covariance matrices and signal propagation in deep neural networks

Many recent works have studied the eigenvalue spectrum of the Conjugate Kernel (CK) defined by the nonlinear feature map of a feedforward neural network. However, existing results only establish weak convergence of the empirical eigenvalue distribution, and fall short of providing precise quantitative characterizations of the ''spike'' eigenvalues and eigenvectors that often capture the low-dimensional signal structure of the learning problem. In this work, we characterize these signal eigenvalues and eigenvectors for a nonlinear version of the spiked covariance model, including the CK as a special case. Using this general result, we give a quantitative description of how spiked eigenstructure in the input data propagates through the hidden layers of a neural network with random weights. As a second application, we study a simple regime of representation learning where the weight matrix develops a rank-one signal component over training and characterize the alignment of the target function with the spike eigenvector of the CK on test data.

Optimal Automated Market Makers: Differentiable Economics and Strong Duality

The role of a market maker is to simultaneously offer to buy and sell quantities of goods, often a financial asset such as a share, at specified prices. An automated market maker (AMM) is a mechanism that offers to trade according to some predetermined schedule; the best choice of this schedule depends on the market maker's goals. The literature on the design of AMMs has mainly focused on prediction markets with the goal of information elicitation. More recent work motivated by DeFi has focused instead on the goal of profit maximization, but considering only a single type of good (traded with a numeraire), including under adverse selection (Milionis et al. 2022). Optimal market making in the presence of multiple goods, including the possibility of complex bundling behavior, is not well understood. In this paper, we show that finding an optimal market maker is dual to an optimal transport problem, with specific geometric constraints on the transport plan in the dual. We show that optimal mechanisms for multiple goods and under adverse selection can take advantage of bundling, both improved prices for bundled purchases and sales as well as sometimes accepting payment "in kind." We present conjectures of optimal mechanisms in additional settings which show further complex behavior. From a methodological perspective, we make essential use of the tools of differentiable economics to generate conjectures of optimal mechanisms, and give a proof-of-concept for the use of such tools in guiding theoretical investigations.

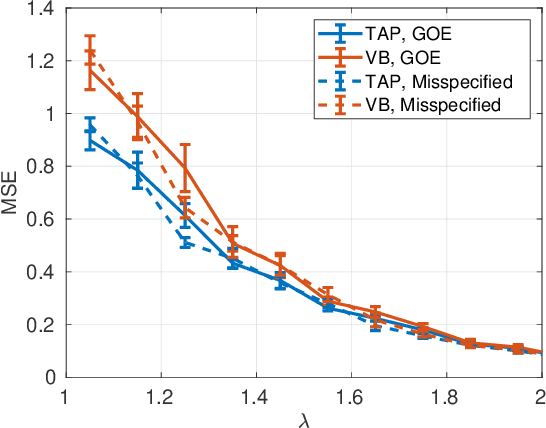
Mean-field variational inference with the TAP free energy: Geometric and statistical properties in linear models

We study mean-field variational inference in a Bayesian linear model when the sample size n is comparable to the dimension p. In high dimensions, the common approach of minimizing a Kullback-Leibler divergence from the posterior distribution, or maximizing an evidence lower bound, may deviate from the true posterior mean and underestimate posterior uncertainty. We study instead minimization of the TAP free energy, showing in a high-dimensional asymptotic framework that it has a local minimizer which provides a consistent estimate of the posterior marginals and may be used for correctly calibrated posterior inference. Geometrically, we show that the landscape of the TAP free energy is strongly convex in an extensive neighborhood of this local minimizer, which under certain general conditions can be found by an Approximate Message Passing (AMP) algorithm. We then exhibit an efficient algorithm that linearly converges to the minimizer within this local neighborhood. In settings where it is conjectured that no efficient algorithm can find this local neighborhood, we prove analogous geometric properties for a local minimizer of the TAP free energy reachable by AMP, and show that posterior inference based on this minimizer remains correctly calibrated.

Transfer Learning for Bayesian Optimization on Heterogeneous Search Spaces

Bayesian optimization (BO) is a popular black-box function optimization method, which makes sequential decisions based on a Bayesian model, typically a Gaussian process (GP), of the function. To ensure the quality of the model, transfer learning approaches have been developed to automatically design GP priors by learning from observations on "training" functions. These training functions are typically required to have the same domain as the "test" function (black-box function to be optimized). In this paper, we introduce MPHD, a model pre-training method on heterogeneous domains, which uses a neural net mapping from domain-specific contexts to specifications of hierarchical GPs. MPHD can be seamlessly integrated with BO to transfer knowledge across heterogeneous search spaces. Our theoretical and empirical results demonstrate the validity of MPHD and its superior performance on challenging black-box function optimization tasks.

HyperBO+: Pre-training a universal prior for Bayesian optimization with hierarchical Gaussian processes

Bayesian optimization (BO), while proved highly effective for many black-box function optimization tasks, requires practitioners to carefully select priors that well model their functions of interest. Rather than specifying by hand, researchers have investigated transfer learning based methods to automatically learn the priors, e.g. multi-task BO (Swersky et al., 2013), few-shot BO (Wistuba and Grabocka, 2021) and HyperBO (Wang et al., 2022). However, those prior learning methods typically assume that the input domains are the same for all tasks, weakening their ability to use observations on functions with different domains or generalize the learned priors to BO on different search spaces. In this work, we present HyperBO+: a pre-training approach for hierarchical Gaussian processes that enables the same prior to work universally for Bayesian optimization on functions with different domains. We propose a two-step pre-training method and analyze its appealing asymptotic properties and benefits to BO both theoretically and empirically. On real-world hyperparameter tuning tasks that involve multiple search spaces, we demonstrate that HyperBO+ is able to generalize to unseen search spaces and achieves lower regrets than competitive baselines.

Local convexity of the TAP free energy and AMP convergence for Z2-synchronization

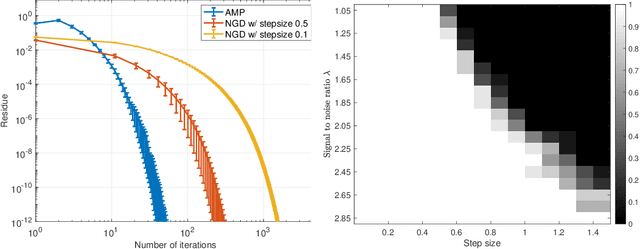
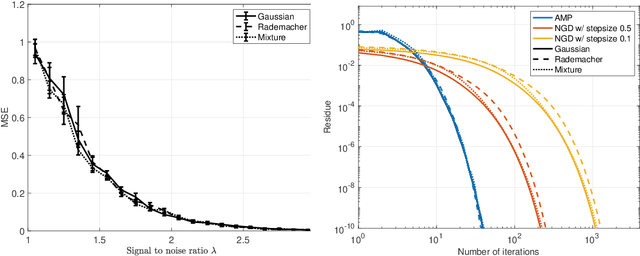
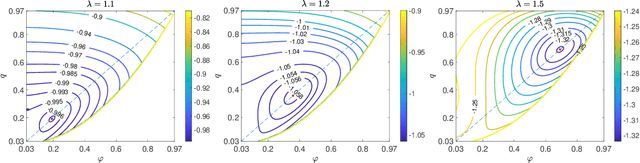
We study mean-field variational Bayesian inference using the TAP approach, for Z2-synchronization as a prototypical example of a high-dimensional Bayesian model. We show that for any signal strength $\lambda > 1$ (the weak-recovery threshold), there exists a unique local minimizer of the TAP free energy functional near the mean of the Bayes posterior law. Furthermore, the TAP free energy in a local neighborhood of this minimizer is strongly convex. Consequently, a natural-gradient/mirror-descent algorithm achieves linear convergence to this minimizer from a local initialization, which may be obtained by a finite number of iterates of Approximate Message Passing (AMP). This provides a rigorous foundation for variational inference in high dimensions via minimization of the TAP free energy. We also analyze the finite-sample convergence of AMP, showing that AMP is asymptotically stable at the TAP minimizer for any $\lambda > 1$, and is linearly convergent to this minimizer from a spectral initialization for sufficiently large $\lambda$. Such a guarantee is stronger than results obtainable by state evolution analyses, which only describe a fixed number of AMP iterations in the infinite-sample limit. Our proofs combine the Kac-Rice formula and Sudakov-Fernique Gaussian comparison inequality to analyze the complexity of critical points that satisfy strong convexity and stability conditions within their local neighborhoods.

Empirical Bayes PCA in high dimensions

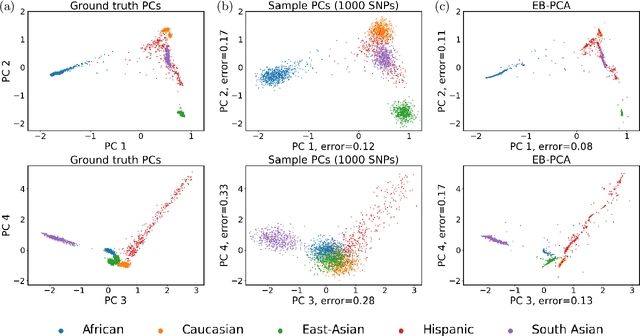
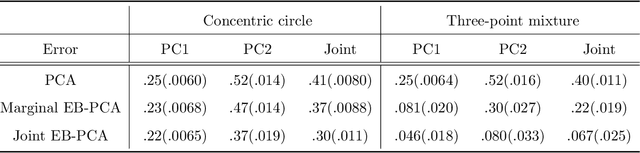
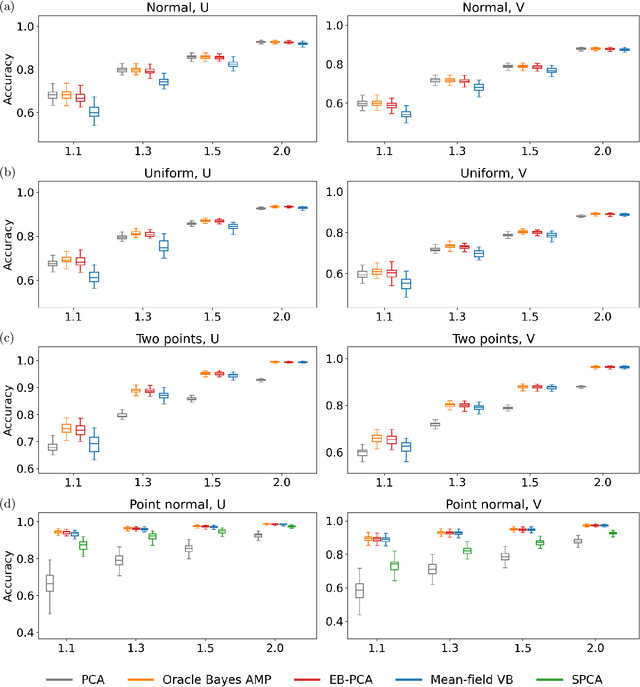
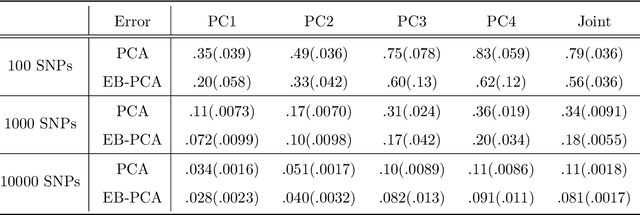
When the dimension of data is comparable to or larger than the number of available data samples, Principal Components Analysis (PCA) is known to exhibit problematic phenomena of high-dimensional noise. In this work, we propose an Empirical Bayes PCA method that reduces this noise by estimating a structural prior for the joint distributions of the principal components. This EB-PCA method is based upon the classical Kiefer-Wolfowitz nonparametric MLE for empirical Bayes estimation, distributional results derived from random matrix theory for the sample PCs, and iterative refinement using an Approximate Message Passing (AMP) algorithm. In theoretical "spiked" models, EB-PCA achieves Bayes-optimal estimation accuracy in the same settings as the oracle Bayes AMP procedure that knows the true priors. Empirically, EB-PCA can substantially improve over PCA when there is strong prior structure, both in simulation and on several quantitative benchmarks constructed using data from the 1000 Genomes Project and the International HapMap Project. A final illustration is presented for an analysis of gene expression data obtained by single-cell RNA-seq.

Spectra of the Conjugate Kernel and Neural Tangent Kernel for linear-width neural networks

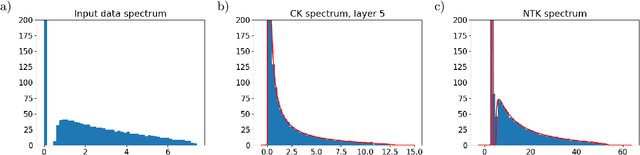
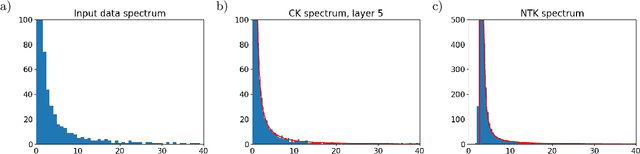
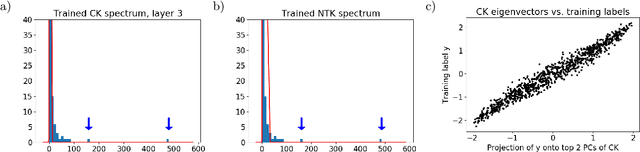
We study the eigenvalue distributions of the Conjugate Kernel and Neural Tangent Kernel associated to multi-layer feedforward neural networks. In an asymptotic regime where network width is increasing linearly in sample size, under random initialization of the weights, and for input samples satisfying a notion of approximate pairwise orthogonality, we show that the eigenvalue distributions of the CK and NTK converge to deterministic limits. The limit for the CK is described by iterating the Marcenko-Pastur map across the hidden layers. The limit for the NTK is equivalent to that of a linear combination of the CK matrices across layers, and may be described by recursive fixed-point equations that extend this Marcenko-Pastur map. We demonstrate the agreement of these asymptotic predictions with the observed spectra for both synthetic and CIFAR-10 training data, and we perform a small simulation to investigate the evolutions of these spectra over training.

Tree-Projected Gradient Descent for Estimating Gradient-Sparse Parameters on Graphs

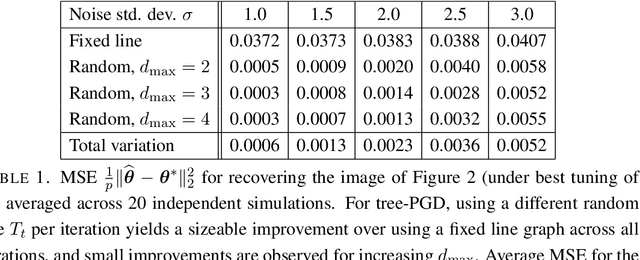
We study estimation of a gradient-sparse parameter vector $\boldsymbol{\theta}^* \in \mathbb{R}^p$, having strong gradient-sparsity $s^*:=\|\nabla_G \boldsymbol{\theta}^*\|_0$ on an underlying graph $G$. Given observations $Z_1,\ldots,Z_n$ and a smooth, convex loss function $\mathcal{L}$ for which $\boldsymbol{\theta}^*$ minimizes the population risk $\mathbb{E}[\mathcal{L}(\boldsymbol{\theta};Z_1,\ldots,Z_n)]$, we propose to estimate $\boldsymbol{\theta}^*$ by a projected gradient descent algorithm that iteratively and approximately projects gradient steps onto spaces of vectors having small gradient-sparsity over low-degree spanning trees of $G$. We show that, under suitable restricted strong convexity and smoothness assumptions for the loss, the resulting estimator achieves the squared-error risk $\frac{s^*}{n} \log (1+\frac{p}{s^*})$ up to a multiplicative constant that is independent of $G$. In contrast, previous polynomial-time algorithms have only been shown to achieve this guarantee in more specialized settings, or under additional assumptions for $G$ and/or the sparsity pattern of $\nabla_G \boldsymbol{\theta}^*$. As applications of our general framework, we apply our results to the examples of linear models and generalized linear models with random design.

Spectral Graph Matching and Regularized Quadratic Relaxations II: Erdős-Rényi Graphs and Universality

We analyze a new spectral graph matching algorithm, GRAph Matching by Pairwise eigen-Alignments (GRAMPA), for recovering the latent vertex correspondence between two unlabeled, edge-correlated weighted graphs. Extending the exact recovery guarantees established in the companion paper for Gaussian weights, in this work, we prove the universality of these guarantees for a general correlated Wigner model. In particular, for two Erd\H{o}s-R\'enyi graphs with edge correlation coefficient $1-\sigma^2$ and average degree at least $\operatorname{polylog}(n)$, we show that GRAMPA exactly recovers the latent vertex correspondence with high probability when $\sigma \lesssim 1/\operatorname{polylog}(n)$. Moreover, we establish a similar guarantee for a variant of GRAMPA, corresponding to a tighter quadratic programming relaxation of the quadratic assignment problem. Our analysis exploits a resolvent representation of the GRAMPA similarity matrix and local laws for the resolvents of sparse Wigner matrices.