GSM-Agent: Understanding Agentic Reasoning Using Controllable Environments

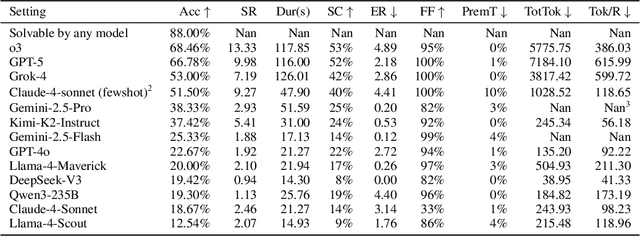
As LLMs are increasingly deployed as agents, agentic reasoning - the ability to combine tool use, especially search, and reasoning - becomes a critical skill. However, it is hard to disentangle agentic reasoning when evaluated in complex environments and tasks. Current agent benchmarks often mix agentic reasoning with challenging math reasoning, expert-level knowledge, and other advanced capabilities. To fill this gap, we build a novel benchmark, GSM-Agent, where an LLM agent is required to solve grade-school-level reasoning problems, but is only presented with the question in the prompt without the premises that contain the necessary information to solve the task, and needs to proactively collect that information using tools. Although the original tasks are grade-school math problems, we observe that even frontier models like GPT-5 only achieve 67% accuracy. To understand and analyze the agentic reasoning patterns, we propose the concept of agentic reasoning graph: cluster the environment's document embeddings into nodes, and map each tool call to its nearest node to build a reasoning path. Surprisingly, we identify that the ability to revisit a previously visited node, widely taken as a crucial pattern in static reasoning, is often missing for agentic reasoning for many models. Based on the insight, we propose a tool-augmented test-time scaling method to improve LLM's agentic reasoning performance by adding tools to encourage models to revisit. We expect our benchmark and the agentic reasoning framework to aid future studies of understanding and pushing the boundaries of agentic reasoning.

Generalization or Hallucination? Understanding Out-of-Context Reasoning in Transformers

Large language models (LLMs) can acquire new knowledge through fine-tuning, but this process exhibits a puzzling duality: models can generalize remarkably from new facts, yet are also prone to hallucinating incorrect information. However, the reasons for this phenomenon remain poorly understood. In this work, we argue that both behaviors stem from a single mechanism known as out-of-context reasoning (OCR): the ability to deduce implications by associating concepts, even those without a causal link. Our experiments across five prominent LLMs confirm that OCR indeed drives both generalization and hallucination, depending on whether the associated concepts are causally related. To build a rigorous theoretical understanding of this phenomenon, we then formalize OCR as a synthetic factual recall task. We empirically show that a one-layer single-head attention-only transformer with factorized output and value matrices can learn to solve this task, while a model with combined weights cannot, highlighting the crucial role of matrix factorization. Our theoretical analysis shows that the OCR capability can be attributed to the implicit bias of gradient descent, which favors solutions that minimize the nuclear norm of the combined output-value matrix. This mathematical structure explains why the model learns to associate facts and implications with high sample efficiency, regardless of whether the correlation is causal or merely spurious. Ultimately, our work provides a theoretical foundation for understanding the OCR phenomenon, offering a new lens for analyzing and mitigating undesirable behaviors from knowledge injection.

SPEED-RL: Faster Training of Reasoning Models via Online Curriculum Learning

Training large language models with reinforcement learning (RL) against verifiable rewards significantly enhances their reasoning abilities, yet remains computationally expensive due to inefficient uniform prompt sampling. We introduce Selective Prompting with Efficient Estimation of Difficulty (SPEED), an adaptive online RL curriculum that selectively chooses training examples of intermediate difficulty to maximize learning efficiency. Theoretically, we establish that intermediate-difficulty prompts improve the gradient estimator's signal-to-noise ratio, accelerating convergence. Empirically, our efficient implementation leads to 2x to 6x faster training without degrading accuracy, requires no manual tuning, and integrates seamlessly into standard RL algorithms.

OVERT: A Benchmark for Over-Refusal Evaluation on Text-to-Image Models

Text-to-Image (T2I) models have achieved remarkable success in generating visual content from text inputs. Although multiple safety alignment strategies have been proposed to prevent harmful outputs, they often lead to overly cautious behavior -- rejecting even benign prompts -- a phenomenon known as $\textit{over-refusal}$ that reduces the practical utility of T2I models. Despite over-refusal having been observed in practice, there is no large-scale benchmark that systematically evaluates this phenomenon for T2I models. In this paper, we present an automatic workflow to construct synthetic evaluation data, resulting in OVERT ($\textbf{OVE}$r-$\textbf{R}$efusal evaluation on $\textbf{T}$ext-to-image models), the first large-scale benchmark for assessing over-refusal behaviors in T2I models. OVERT includes 4,600 seemingly harmful but benign prompts across nine safety-related categories, along with 1,785 genuinely harmful prompts (OVERT-unsafe) to evaluate the safety-utility trade-off. Using OVERT, we evaluate several leading T2I models and find that over-refusal is a widespread issue across various categories (Figure 1), underscoring the need for further research to enhance the safety alignment of T2I models without compromising their functionality. As a preliminary attempt to reduce over-refusal, we explore prompt rewriting; however, we find it often compromises faithfulness to the meaning of the original prompts. Finally, we demonstrate the flexibility of our generation framework in accommodating diverse safety requirements by generating customized evaluation data adapting to user-defined policies.

Improving LLM Safety Alignment with Dual-Objective Optimization

Existing training-time safety alignment techniques for large language models (LLMs) remain vulnerable to jailbreak attacks. Direct preference optimization (DPO), a widely deployed alignment method, exhibits limitations in both experimental and theoretical contexts as its loss function proves suboptimal for refusal learning. Through gradient-based analysis, we identify these shortcomings and propose an improved safety alignment that disentangles DPO objectives into two components: (1) robust refusal training, which encourages refusal even when partial unsafe generations are produced, and (2) targeted unlearning of harmful knowledge. This approach significantly increases LLM robustness against a wide range of jailbreak attacks, including prefilling, suffix, and multi-turn attacks across both in-distribution and out-of-distribution scenarios. Furthermore, we introduce a method to emphasize critical refusal tokens by incorporating a reward-based token-level weighting mechanism for refusal learning, which further improves the robustness against adversarial exploits. Our research also suggests that robustness to jailbreak attacks is correlated with token distribution shifts in the training process and internal representations of refusal and harmful tokens, offering valuable directions for future research in LLM safety alignment. The code is available at https://github.com/wicai24/DOOR-Alignment

An Overview of Large Language Models for Statisticians

Large Language Models (LLMs) have emerged as transformative tools in artificial intelligence (AI), exhibiting remarkable capabilities across diverse tasks such as text generation, reasoning, and decision-making. While their success has primarily been driven by advances in computational power and deep learning architectures, emerging problems -- in areas such as uncertainty quantification, decision-making, causal inference, and distribution shift -- require a deeper engagement with the field of statistics. This paper explores potential areas where statisticians can make important contributions to the development of LLMs, particularly those that aim to engender trustworthiness and transparency for human users. Thus, we focus on issues such as uncertainty quantification, interpretability, fairness, privacy, watermarking and model adaptation. We also consider possible roles for LLMs in statistical analysis. By bridging AI and statistics, we aim to foster a deeper collaboration that advances both the theoretical foundations and practical applications of LLMs, ultimately shaping their role in addressing complex societal challenges.

Implicit Bias of Gradient Descent for Non-Homogeneous Deep Networks

We establish the asymptotic implicit bias of gradient descent (GD) for generic non-homogeneous deep networks under exponential loss. Specifically, we characterize three key properties of GD iterates starting from a sufficiently small empirical risk, where the threshold is determined by a measure of the network's non-homogeneity. First, we show that a normalized margin induced by the GD iterates increases nearly monotonically. Second, we prove that while the norm of the GD iterates diverges to infinity, the iterates themselves converge in direction. Finally, we establish that this directional limit satisfies the Karush-Kuhn-Tucker (KKT) conditions of a margin maximization problem. Prior works on implicit bias have focused exclusively on homogeneous networks; in contrast, our results apply to a broad class of non-homogeneous networks satisfying a mild near-homogeneity condition. In particular, our results apply to networks with residual connections and non-homogeneous activation functions, thereby resolving an open problem posed by Ji and Telgarsky (2020).

How Do LLMs Perform Two-Hop Reasoning in Context?

"Socrates is human. All humans are mortal. Therefore, Socrates is mortal." This classical example demonstrates two-hop reasoning, where a conclusion logically follows from two connected premises. While transformer-based Large Language Models (LLMs) can make two-hop reasoning, they tend to collapse to random guessing when faced with distracting premises. To understand the underlying mechanism, we train a three-layer transformer on synthetic two-hop reasoning tasks. The training dynamics show two stages: a slow learning phase, where the 3-layer transformer performs random guessing like LLMs, followed by an abrupt phase transitions, where the 3-layer transformer suddenly reaches $100%$ accuracy. Through reverse engineering, we explain the inner mechanisms for how models learn to randomly guess between distractions initially, and how they learn to ignore distractions eventually. We further propose a three-parameter model that supports the causal claims for the mechanisms to the training dynamics of the transformer. Finally, experiments on LLMs suggest that the discovered mechanisms generalize across scales. Our methodologies provide new perspectives for scientific understandings of LLMs and our findings provide new insights into how reasoning emerges during training.

A Statistical Theory of Contrastive Pre-training and Multimodal Generative AI

Multi-modal generative AI systems, such as those combining vision and language, rely on contrastive pre-training to learn representations across different modalities. While their practical benefits are widely acknowledged, a rigorous theoretical understanding of the contrastive pre-training framework remains limited. This paper develops a theoretical framework to explain the success of contrastive pre-training in downstream tasks, such as zero-shot classification, conditional diffusion models, and vision-language models. We introduce the concept of approximate sufficient statistics, a generalization of the classical sufficient statistics, and show that near-minimizers of the contrastive pre-training loss are approximately sufficient, making them adaptable to diverse downstream tasks. We further propose the Joint Generative Hierarchical Model for the joint distribution of images and text, showing that transformers can efficiently approximate relevant functions within this model via belief propagation. Building on this framework, we derive sample complexity guarantees for multi-modal learning based on contrastive pre-trained representations. Numerical simulations validate these theoretical findings, demonstrating the strong generalization performance of contrastively pre-trained transformers in various multi-modal tasks.

Active-Dormant Attention Heads: Mechanistically Demystifying Extreme-Token Phenomena in LLMs

Practitioners have consistently observed three puzzling phenomena in transformer-based large language models (LLMs): attention sinks, value-state drains, and residual-state peaks, collectively referred to as extreme-token phenomena. These phenomena are characterized by certain so-called "sink tokens" receiving disproportionately high attention weights, exhibiting significantly smaller value states, and having much larger residual-state norms than those of other tokens. These extreme tokens give rise to various challenges in LLM inference, quantization, and interpretability. We elucidate the mechanisms behind extreme-token phenomena. First, we show that these phenomena arise in very simple architectures -- transformers with one to three layers -- trained on a toy model, the Bigram-Backcopy (BB) task. In this setting, we identify an active-dormant mechanism, where attention heads become sinks for specific input domains while remaining non-sinks for others. Our theoretical analysis of the training dynamics reveals that these phenomena are driven by a mutual reinforcement mechanism. Building on these insights, we propose strategies to mitigate extreme-token phenomena during pretraining, including replacing softmax with ReLU and Adam with SGD. Next, we extend our analysis to pretrained LLMs, including Llama and OLMo, showing that many attention heads exhibit a similar active-dormant mechanism as in the BB task, and that the mutual reinforcement mechanism also governs the emergence of extreme-token phenomena during LLM pretraining. Our results reveal that many of the static and dynamic properties of extreme-token phenomena predicted by the BB task align with observations in pretrained LLMs.