Leveraging the Hints: Adaptive Bidding in Repeated First-Price Auctions

With the advent and increasing consolidation of e-commerce, digital advertising has very recently replaced traditional advertising as the main marketing force in the economy. In the past four years, a particularly important development in the digital advertising industry is the shift from second-price auctions to first-price auctions for online display ads. This shift immediately motivated the intellectually challenging question of how to bid in first-price auctions, because unlike in second-price auctions, bidding one's private value truthfully is no longer optimal. Following a series of recent works in this area, we consider a differentiated setup: we do not make any assumption about other bidders' maximum bid (i.e. it can be adversarial over time), and instead assume that we have access to a hint that serves as a prediction of other bidders' maximum bid, where the prediction is learned through some blackbox machine learning model. We consider two types of hints: one where a single point-prediction is available, and the other where a hint interval (representing a type of confidence region into which others' maximum bid falls) is available. We establish minimax optimal regret bounds for both cases and highlight the quantitatively different behavior between the two settings. We also provide improved regret bounds when the others' maximum bid exhibits the further structure of sparsity. Finally, we complement the theoretical results with demonstrations using real bidding data.

Distributionally Robust Offline Reinforcement Learning with Linear Function Approximation

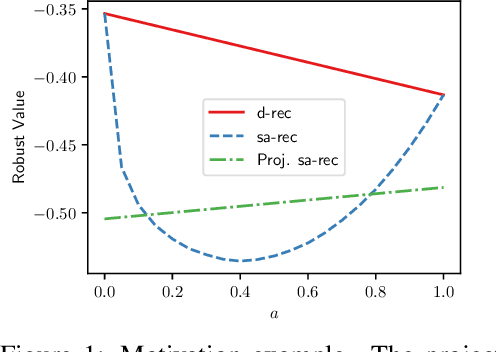
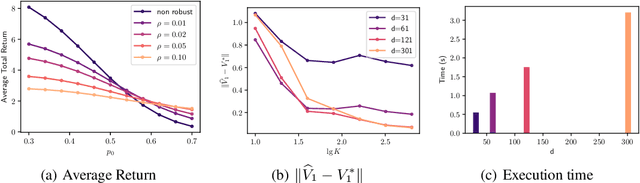
Among the reasons hindering reinforcement learning (RL) applications to real-world problems, two factors are critical: limited data and the mismatch between the testing environment (real environment in which the policy is deployed) and the training environment (e.g., a simulator). This paper attempts to address these issues simultaneously with distributionally robust offline RL, where we learn a distributionally robust policy using historical data obtained from the source environment by optimizing against a worst-case perturbation thereof. In particular, we move beyond tabular settings and consider linear function approximation. More specifically, we consider two settings, one where the dataset is well-explored and the other where the dataset has sufficient coverage. We propose two algorithms -- one for each of the two settings -- that achieve error bounds $\tilde{O}(d^{1/2}/N^{1/2})$ and $\tilde{O}(d^{3/2}/N^{1/2})$ respectively, where $d$ is the dimension in the linear function approximation and $N$ is the number of trajectories in the dataset. To the best of our knowledge, they provide the first non-asymptotic results of the sample complexity in this setting. Diverse experiments are conducted to demonstrate our theoretical findings, showing the superiority of our algorithm against the non-robust one.

Optimal Diagonal Preconditioning: Theory and Practice

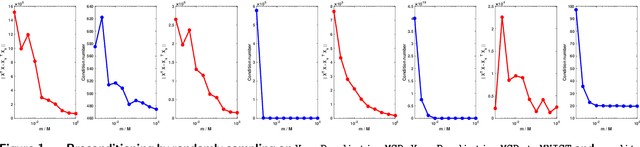
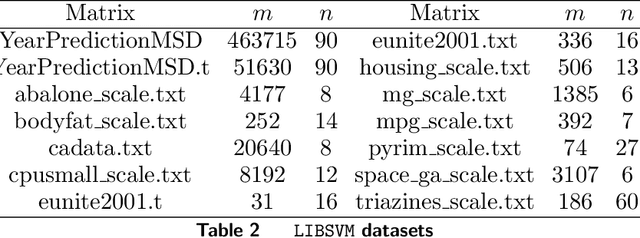
Preconditioning has been a staple technique in optimization and machine learning. It often reduces the condition number of the matrix it is applied to, thereby speeding up convergence of optimization algorithms. Although there are many popular preconditioning techniques in practice, most lack theoretical guarantees for reductions in condition number. In this paper, we study the problem of optimal diagonal preconditioning to achieve maximal reduction in the condition number of any full-rank matrix by scaling its rows or columns separately or simultaneously. We first reformulate the problem as a quasi-convex problem and provide a baseline bisection algorithm that is easy to implement in practice, where each iteration consists of an SDP feasibility problem. Then we propose a polynomial time potential reduction algorithm with $O(\log(\frac{1}{\epsilon}))$ iteration complexity, where each iteration consists of a Newton update based on the Nesterov-Todd direction. Our algorithm is based on a formulation of the problem which is a generalized version of the Von Neumann optimal growth problem. Next, we specialize to one-sided optimal diagonal preconditioning problems, and demonstrate that they can be formulated as standard dual SDP problems, to which we apply efficient customized solvers and study the empirical performance of our optimal diagonal preconditioners. Our extensive experiments on large matrices demonstrate the practical appeal of optimal diagonal preconditioners at reducing condition numbers compared to heuristics-based preconditioners.

Learning to Order for Inventory Systems with Lost Sales and Uncertain Supplies

We consider a stochastic lost-sales inventory control system with a lead time $L$ over a planning horizon $T$. Supply is uncertain, and is a function of the order quantity (due to random yield/capacity, etc). We aim to minimize the $T$-period cost, a problem that is known to be computationally intractable even under known distributions of demand and supply. In this paper, we assume that both the demand and supply distributions are unknown and develop a computationally efficient online learning algorithm. We show that our algorithm achieves a regret (i.e. the performance gap between the cost of our algorithm and that of an optimal policy over $T$ periods) of $O(L+\sqrt{T})$ when $L\geq\log(T)$. We do so by 1) showing our algorithm cost is higher by at most $O(L+\sqrt{T})$ for any $L\geq 0$ compared to an optimal constant-order policy under complete information (a well-known and widely-used algorithm) and 2) leveraging its known performance guarantee from the existing literature. To the best of our knowledge, a finite-sample $O(\sqrt{T})$ (and polynomial in $L$) regret bound when benchmarked against an optimal policy is not known before in the online inventory control literature. A key challenge in this learning problem is that both demand and supply data can be censored; hence only truncated values are observable. We circumvent this challenge by showing that the data generated under an order quantity $q^2$ allows us to simulate the performance of not only $q^2$ but also $q^1$ for all $q^1<q^2$, a key observation to obtain sufficient information even under data censoring. By establishing a high probability coupling argument, we are able to evaluate and compare the performance of different order policies at their steady state within a finite time horizon. Since the problem lacks convexity, we develop an active elimination method that adaptively rules out suboptimal solutions.

Doubly Robust Distributionally Robust Off-Policy Evaluation and Learning

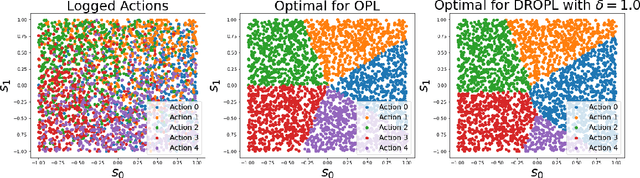
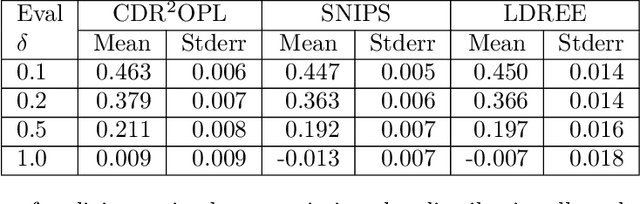
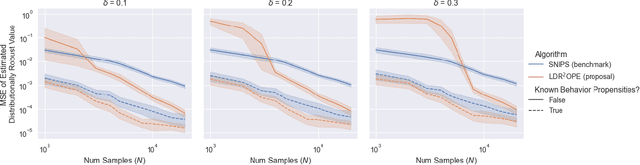
Off-policy evaluation and learning (OPE/L) use offline observational data to make better decisions, which is crucial in applications where experimentation is necessarily limited. OPE/L is nonetheless sensitive to discrepancies between the data-generating environment and that where policies are deployed. Recent work proposed distributionally robust OPE/L (DROPE/L) to remedy this, but the proposal relies on inverse-propensity weighting, whose regret rates may deteriorate if propensities are estimated and whose variance is suboptimal even if not. For vanilla OPE/L, this is solved by doubly robust (DR) methods, but they do not naturally extend to the more complex DROPE/L, which involves a worst-case expectation. In this paper, we propose the first DR algorithms for DROPE/L with KL-divergence uncertainty sets. For evaluation, we propose Localized Doubly Robust DROPE (LDR$^2$OPE) and prove its semiparametric efficiency under weak product rates conditions. Notably, thanks to a localization technique, LDR$^2$OPE only requires fitting a small number of regressions, just like DR methods for vanilla OPE. For learning, we propose Continuum Doubly Robust DROPL (CDR$^2$OPL) and show that, under a product rate condition involving a continuum of regressions, it enjoys a fast regret rate of $\mathcal{O}(N^{-1/2})$ even when unknown propensities are nonparametrically estimated. We further extend our results to general $f$-divergence uncertainty sets. We illustrate the advantage of our algorithms in simulations.

Optimal No-Regret Learning in Strongly Monotone Games with Bandit Feedback

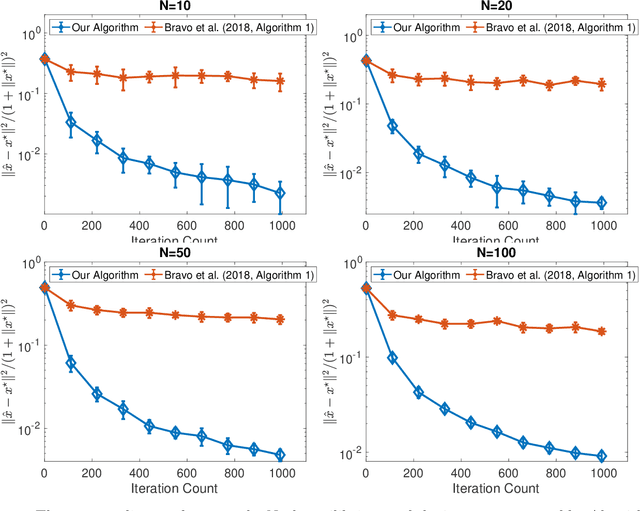
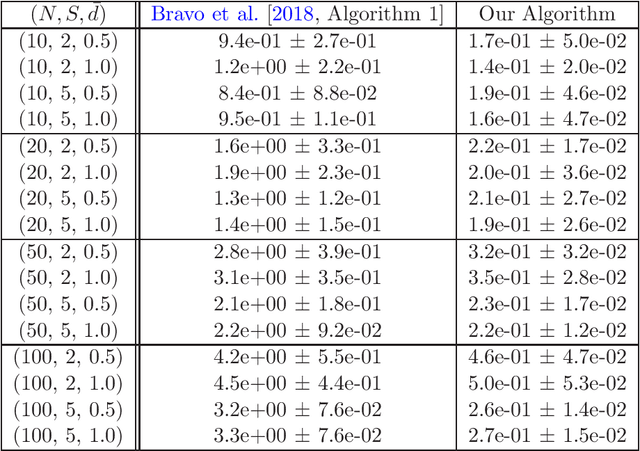
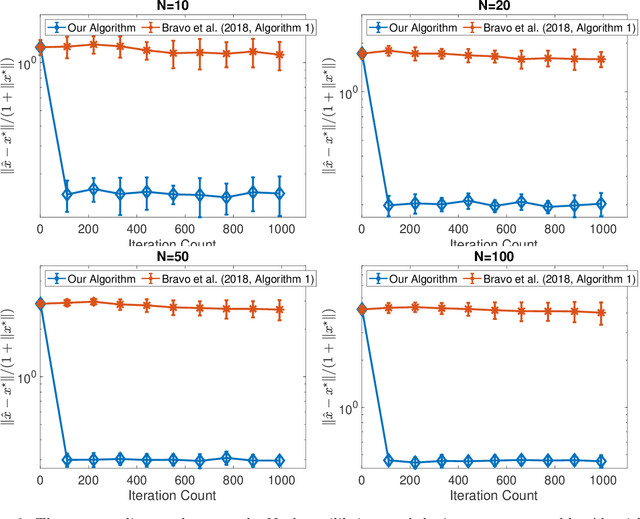
We consider online no-regret learning in unknown games with bandit feedback, where each agent only observes its reward at each time -- determined by all players' current joint action -- rather than its gradient. We focus on the class of smooth and strongly monotone games and study optimal no-regret learning therein. Leveraging self-concordant barrier functions, we first construct an online bandit convex optimization algorithm and show that it achieves the single-agent optimal regret of $\tilde{\Theta}(\sqrt{T})$ under smooth and strongly-concave payoff functions. We then show that if each agent applies this no-regret learning algorithm in strongly monotone games, the joint action converges in \textit{last iterate} to the unique Nash equilibrium at a rate of $\tilde{\Theta}(1/\sqrt{T})$. Prior to our work, the best-know convergence rate in the same class of games is $O(1/T^{1/3})$ (achieved by a different algorithm), thus leaving open the problem of optimal no-regret learning algorithms (since the known lower bound is $\Omega(1/\sqrt{T})$). Our results thus settle this open problem and contribute to the broad landscape of bandit game-theoretical learning by identifying the first doubly optimal bandit learning algorithm, in that it achieves (up to log factors) both optimal regret in the single-agent learning and optimal last-iterate convergence rate in the multi-agent learning. We also present results on several simulation studies -- Cournot competition, Kelly auctions, and distributed regularized logistic regression -- to demonstrate the efficacy of our algorithm.

Computational Benefits of Intermediate Rewards for Hierarchical Planning

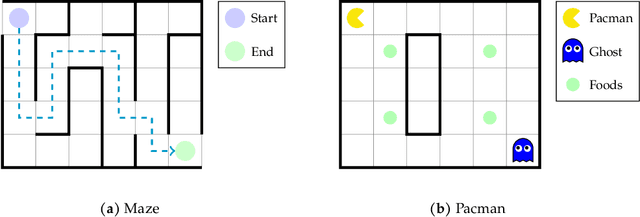
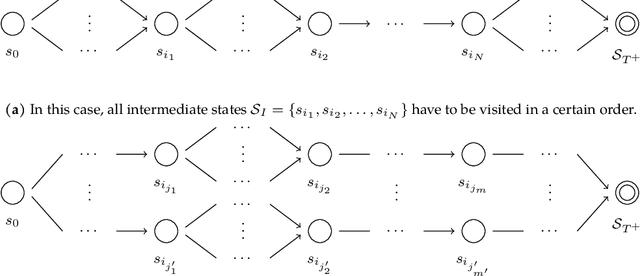
Many hierarchical reinforcement learning (RL) applications have empirically verified that incorporating prior knowledge in reward design improves convergence speed and practical performance. We attempt to quantify the computational benefits of hierarchical RL from a planning perspective under assumptions about the intermediate state and intermediate rewards frequently (but often implicitly) adopted in practice. Our approach reveals a trade-off between computational complexity and the pursuit of the shortest path in hierarchical planning: using intermediate rewards significantly reduces the computational complexity in finding a successful policy but does not guarantee to find the shortest path, whereas using sparse terminal rewards finds the shortest path at a significantly higher computational cost. We also corroborate our theoretical results with extensive experiments on the MiniGrid environments using Q-learning and other popular deep RL algorithms.

Distributed stochastic optimization with large delays

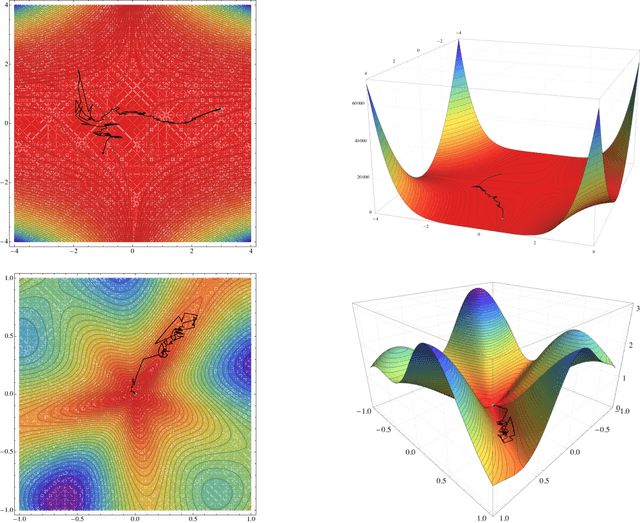
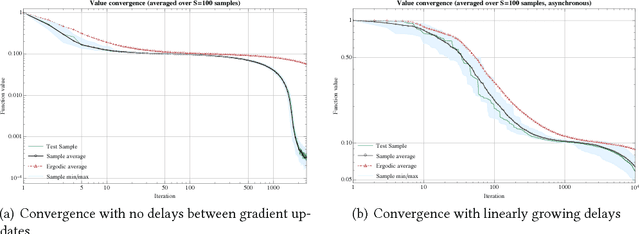
One of the most widely used methods for solving large-scale stochastic optimization problems is distributed asynchronous stochastic gradient descent (DASGD), a family of algorithms that result from parallelizing stochastic gradient descent on distributed computing architectures (possibly) asychronously. However, a key obstacle in the efficient implementation of DASGD is the issue of delays: when a computing node contributes a gradient update, the global model parameter may have already been updated by other nodes several times over, thereby rendering this gradient information stale. These delays can quickly add up if the computational throughput of a node is saturated, so the convergence of DASGD may be compromised in the presence of large delays. Our first contribution is that, by carefully tuning the algorithm's step-size, convergence to the critical set is still achieved in mean square, even if the delays grow unbounded at a polynomial rate. We also establish finer results in a broad class of structured optimization problems (called variationally coherent), where we show that DASGD converges to a global optimum with probability $1$ under the same delay assumptions. Together, these results contribute to the broad landscape of large-scale non-convex stochastic optimization by offering state-of-the-art theoretical guarantees and providing insights for algorithm design.

Policy Learning with Adaptively Collected Data

Learning optimal policies from historical data enables the gains from personalization to be realized in a wide variety of applications. The growing policy learning literature focuses on a setting where the treatment assignment policy does not adapt to the data. However, adaptive data collection is becoming more common in practice, from two primary sources: 1) data collected from adaptive experiments that are designed to improve inferential efficiency; 2) data collected from production systems that are adaptively evolving an operational policy to improve performance over time (e.g. contextual bandits). In this paper, we aim to address the challenge of learning the optimal policy with adaptively collected data and provide one of the first theoretical inquiries into this problem. We propose an algorithm based on generalized augmented inverse propensity weighted estimators and establish its finite-sample regret bound. We complement this regret upper bound with a lower bound that characterizes the fundamental difficulty of policy learning with adaptive data. Finally, we demonstrate our algorithm's effectiveness using both synthetic data and public benchmark datasets.

Simple Agent, Complex Environment: Efficient Reinforcement Learning with Agent State

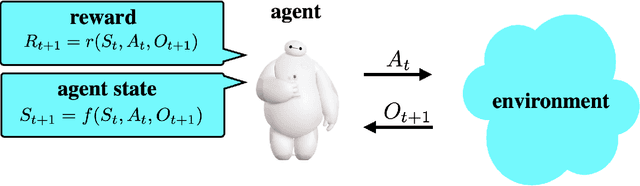
We design a simple reinforcement learning agent that, with a specification only of agent state dynamics and a reward function, can operate with some degree of competence in any environment. The agent maintains only visitation counts and value estimates for each agent-state-action pair. The value function is updated incrementally in response to temporal differences and optimistic boosts that encourage exploration. The agent executes actions that are greedy with respect to this value function. We establish a regret bound demonstrating convergence to near-optimal per-period performance, where the time taken to achieve near-optimality is polynomial in the number of agent states and actions, as well as the reward mixing time of the best policy within the reference policy class, which is comprised of those that depend on history only through agent state. Notably, there is no further dependence on the number of environment states or mixing times associated with other policies or statistics of history. Our result sheds light on the potential benefits of (deep) representation learning, which has demonstrated the capability to extract compact and relevant features from high-dimensional interaction histories.