Optimal Diagonal Preconditioning: Theory and Practice
Paper and Code
Sep 02, 2022
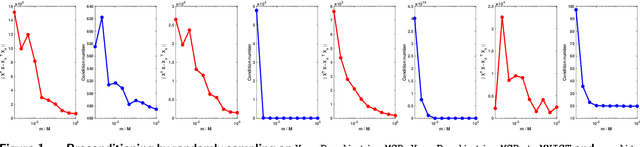
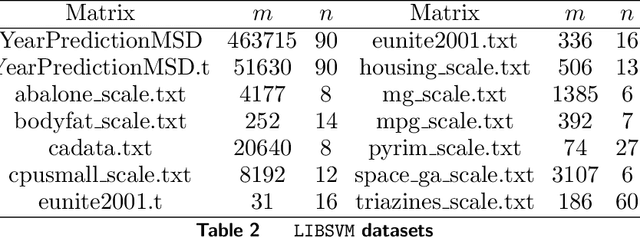

Preconditioning has been a staple technique in optimization and machine learning. It often reduces the condition number of the matrix it is applied to, thereby speeding up convergence of optimization algorithms. Although there are many popular preconditioning techniques in practice, most lack theoretical guarantees for reductions in condition number. In this paper, we study the problem of optimal diagonal preconditioning to achieve maximal reduction in the condition number of any full-rank matrix by scaling its rows or columns separately or simultaneously. We first reformulate the problem as a quasi-convex problem and provide a baseline bisection algorithm that is easy to implement in practice, where each iteration consists of an SDP feasibility problem. Then we propose a polynomial time potential reduction algorithm with $O(\log(\frac{1}{\epsilon}))$ iteration complexity, where each iteration consists of a Newton update based on the Nesterov-Todd direction. Our algorithm is based on a formulation of the problem which is a generalized version of the Von Neumann optimal growth problem. Next, we specialize to one-sided optimal diagonal preconditioning problems, and demonstrate that they can be formulated as standard dual SDP problems, to which we apply efficient customized solvers and study the empirical performance of our optimal diagonal preconditioners. Our extensive experiments on large matrices demonstrate the practical appeal of optimal diagonal preconditioners at reducing condition numbers compared to heuristics-based preconditioners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge