Learning to Control Unknown Strongly Monotone Games

Consider $N$ players each with a $d$-dimensional action set. Each of the players' utility functions includes their reward function and a linear term for each dimension, with coefficients that are controlled by the manager. We assume that the game is strongly monotone, so if each player runs gradient descent, the dynamics converge to a unique Nash equilibrium (NE). The NE is typically inefficient in terms of global performance. The resulting global performance of the system can be improved by imposing $K$-dimensional linear constraints on the NE. We therefore want the manager to pick the controlled coefficients that impose the desired constraint on the NE. However, this requires knowing the players' reward functions and their action sets. Obtaining this game structure information is infeasible in a large-scale network and violates the users' privacy. To overcome this, we propose a simple algorithm that learns to shift the NE of the game to meet the linear constraints by adjusting the controlled coefficients online. Our algorithm only requires the linear constraints violation as feedback and does not need to know the reward functions or the action sets. We prove that our algorithm, which is based on two time-scale stochastic approximation, guarantees convergence with probability 1 to the set of NE that meet target linear constraints. We then provide a mean square convergence rate of $O(t^{-1/4})$ for our algorithm. This is the first such bound for two time-scale stochastic approximation where the slower time-scale is a fixed point iteration with a non-expansive mapping. We demonstrate how our scheme can be applied to optimizing a global quadratic cost at NE and load balancing in resource allocation games. We provide simulations of our algorithm for these scenarios.

Payoff-based learning with matrix multiplicative weights in quantum games

In this paper, we study the problem of learning in quantum games - and other classes of semidefinite games - with scalar, payoff-based feedback. For concreteness, we focus on the widely used matrix multiplicative weights (MMW) algorithm and, instead of requiring players to have full knowledge of the game (and/or each other's chosen states), we introduce a suite of minimal-information matrix multiplicative weights (3MW) methods tailored to different information frameworks. The main difficulty to attaining convergence in this setting is that, in contrast to classical finite games, quantum games have an infinite continuum of pure states (the quantum equivalent of pure strategies), so standard importance-weighting techniques for estimating payoff vectors cannot be employed. Instead, we borrow ideas from bandit convex optimization and we design a zeroth-order gradient sampler adapted to the semidefinite geometry of the problem at hand. As a first result, we show that the 3MW method with deterministic payoff feedback retains the $\mathcal{O}(1/\sqrt{T})$ convergence rate of the vanilla, full information MMW algorithm in quantum min-max games, even though the players only observe a single scalar. Subsequently, we relax the algorithm's information requirements even further and we provide a 3MW method that only requires players to observe a random realization of their payoff observable, and converges to equilibrium at an $\mathcal{O}(T^{-1/4})$ rate. Finally, going beyond zero-sum games, we show that a regularized variant of the proposed 3MW method guarantees local convergence with high probability to all equilibria that satisfy a certain first-order stability condition.

Equilibrium Bandits: Learning Optimal Equilibria of Unknown Dynamics

Consider a decision-maker that can pick one out of $K$ actions to control an unknown system, for $T$ turns. The actions are interpreted as different configurations or policies. Holding the same action fixed, the system asymptotically converges to a unique equilibrium, as a function of this action. The dynamics of the system are unknown to the decision-maker, which can only observe a noisy reward at the end of every turn. The decision-maker wants to maximize its accumulated reward over the $T$ turns. Learning what equilibria are better results in higher rewards, but waiting for the system to converge to equilibrium costs valuable time. Existing bandit algorithms, either stochastic or adversarial, achieve linear (trivial) regret for this problem. We present a novel algorithm, termed Upper Equilibrium Concentration Bound (UECB), that knows to switch an action quickly if it is not worth it to wait until the equilibrium is reached. This is enabled by employing convergence bounds to determine how far the system is from equilibrium. We prove that UECB achieves a regret of $\mathcal{O}(\log(T)+\tau_c\log(\tau_c)+\tau_c\log\log(T))$ for this equilibrium bandit problem where $\tau_c$ is the worst case approximate convergence time to equilibrium. We then show that both epidemic control and game control are special cases of equilibrium bandits, where $\tau_c\log \tau_c$ typically dominates the regret. We then test UECB numerically for both of these applications.

Learning in quantum games

In this paper, we introduce a class of learning dynamics for general quantum games, that we call "follow the quantum regularized leader" (FTQL), in reference to the classical "follow the regularized leader" (FTRL) template for learning in finite games. We show that the induced quantum state dynamics decompose into (i) a classical, commutative component which governs the dynamics of the system's eigenvalues in a way analogous to the evolution of mixed strategies under FTRL; and (ii) a non-commutative component for the system's eigenvectors which has no classical counterpart. Despite the complications that this non-classical component entails, we find that the FTQL dynamics incur no more than constant regret in all quantum games. Moreover, adjusting classical notions of stability to account for the nonlinear geometry of the state space of quantum games, we show that only pure quantum equilibria can be stable and attracting under FTQL while, as a partial converse, pure equilibria that satisfy a certain "variational stability" condition are always attracting. Finally, we show that the FTQL dynamics are Poincar\'e recurrent in quantum min-max games, extending in this way a very recent result for the quantum replicator dynamics.

Distributed stochastic optimization with large delays

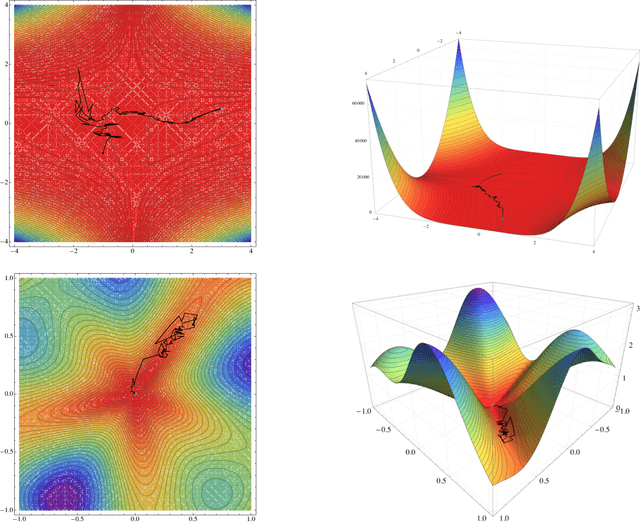
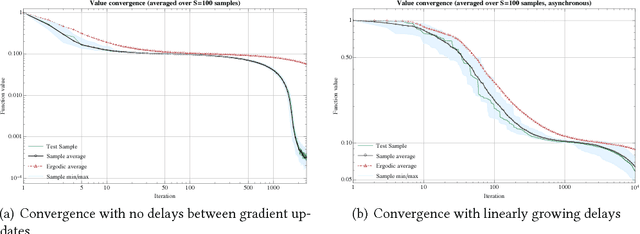
One of the most widely used methods for solving large-scale stochastic optimization problems is distributed asynchronous stochastic gradient descent (DASGD), a family of algorithms that result from parallelizing stochastic gradient descent on distributed computing architectures (possibly) asychronously. However, a key obstacle in the efficient implementation of DASGD is the issue of delays: when a computing node contributes a gradient update, the global model parameter may have already been updated by other nodes several times over, thereby rendering this gradient information stale. These delays can quickly add up if the computational throughput of a node is saturated, so the convergence of DASGD may be compromised in the presence of large delays. Our first contribution is that, by carefully tuning the algorithm's step-size, convergence to the critical set is still achieved in mean square, even if the delays grow unbounded at a polynomial rate. We also establish finer results in a broad class of structured optimization problems (called variationally coherent), where we show that DASGD converges to a global optimum with probability $1$ under the same delay assumptions. Together, these results contribute to the broad landscape of large-scale non-convex stochastic optimization by offering state-of-the-art theoretical guarantees and providing insights for algorithm design.

No Discounted-Regret Learning in Adversarial Bandits with Delays

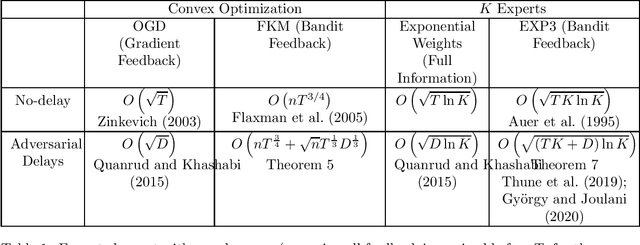
Consider a player that in each round $t$ out of $T$ rounds chooses an action and observes the incurred cost after a delay of $d_{t}$ rounds. The cost functions and the delay sequence are chosen by an adversary. We show that even if the players' algorithms lose their "no regret" property due to too large delays, the expected discounted ergodic distribution of play converges to the set of coarse correlated equilibrium (CCE) if the algorithms have "no discounted-regret". For a zero-sum game, we show that no discounted-regret is sufficient for the discounted ergodic average of play to converge to the set of Nash equilibria. We prove that the FKM algorithm with $n$ dimensions achieves a regret of $O\left(nT^{\frac{3}{4}}+\sqrt{n}T^{\frac{1}{3}}D^{\frac{1}{3}}\right)$ and the EXP3 algorithm with $K$ arms achieves a regret of $O\left(\sqrt{\ln K\left(KT+D\right)}\right)$ even when $D=\sum_{t=1}^{T}d_{t}$ and $T$ are unknown. These bounds use a novel doubling trick that provably retains the regret bound for when $D$ and $T$ are known. Using these bounds, we show that EXP3 and FKM have no discounted-regret even for $d_{t}=O\left(t\log t\right)$. Therefore, the CCE of a finite or convex unknown game can be approximated even when only delayed bandit feedback is available via simulation.

My Fair Bandit: Distributed Learning of Max-Min Fairness with Multi-player Bandits

Consider N cooperative but non-communicating players where each plays one out of M arms for T turns. Players have different utilities for each arm, representable as an NxM matrix. These utilities are unknown to the players. In each turn players select an arm and receive a noisy observation of their utility for it. However, if any other players selected the same arm that turn, all colliding players will all receive zero utility due to the conflict. No other communication or coordination between the players is possible. Our goal is to design a distributed algorithm that learns the matching between players and arms that achieves max-min fairness while minimizing the regret. We present an algorithm and prove that it is regret optimal up to a $\log\log T$ factor. This is the first max-min fairness multi-player bandit algorithm with (near) order optimal regret.

On the convergence of mirror descent beyond stochastic convex programming

In this paper, we examine the convergence of mirror descent in a class of stochastic optimization problems that are not necessarily convex (or even quasi-convex), and which we call variationally coherent. Since the standard technique of "ergodic averaging" offers no tangible benefits beyond convex programming, we focus directly on the algorithm's last generated sample (its "last iterate"), and we show that it converges with probabiility $1$ if the underlying problem is coherent. We further consider a localized version of variational coherence which ensures local convergence of stochastic mirror descent (SMD) with high probability. These results contribute to the landscape of non-convex stochastic optimization by showing that (quasi-)convexity is not essential for convergence to a global minimum: rather, variational coherence, a much weaker requirement, suffices. Finally, building on the above, we reveal an interesting insight regarding the convergence speed of SMD: in problems with sharp minima (such as generic linear programs or concave minimization problems), SMD reaches a minimum point in a finite number of steps (a.s.), even in the presence of persistent gradient noise. This result is to be contrasted with existing black-box convergence rate estimates that are only asymptotic.