Contextual Linear Optimization with Bandit Feedback

Contextual linear optimization (CLO) uses predictive observations to reduce uncertainty in random cost coefficients and thereby improve average-cost performance. An example is a stochastic shortest path with random edge costs (e.g., traffic) and predictive features (e.g., lagged traffic, weather). Existing work on CLO assumes the data has fully observed cost coefficient vectors, but in many applications, we can only see the realized cost of a historical decision, that is, just one projection of the random cost coefficient vector, to which we refer as bandit feedback. We study a class of algorithms for CLO with bandit feedback, which we term induced empirical risk minimization (IERM), where we fit a predictive model to directly optimize the downstream performance of the policy it induces. We show a fast-rate regret bound for IERM that allows for misspecified model classes and flexible choices of the optimization estimate, and we develop computationally tractable surrogate losses. A byproduct of our theory of independent interest is fast-rate regret bound for IERM with full feedback and misspecified policy class. We compare the performance of different modeling choices numerically using a stochastic shortest path example and provide practical insights from the empirical results.

Source Condition Double Robust Inference on Functionals of Inverse Problems

We consider estimation of parameters defined as linear functionals of solutions to linear inverse problems. Any such parameter admits a doubly robust representation that depends on the solution to a dual linear inverse problem, where the dual solution can be thought as a generalization of the inverse propensity function. We provide the first source condition double robust inference method that ensures asymptotic normality around the parameter of interest as long as either the primal or the dual inverse problem is sufficiently well-posed, without knowledge of which inverse problem is the more well-posed one. Our result is enabled by novel guarantees for iterated Tikhonov regularized adversarial estimators for linear inverse problems, over general hypothesis spaces, which are developments of independent interest.

Learning under Selective Labels with Data from Heterogeneous Decision-makers: An Instrumental Variable Approach

We study the problem of learning with selectively labeled data, which arises when outcomes are only partially labeled due to historical decision-making. The labeled data distribution may substantially differ from the full population, especially when the historical decisions and the target outcome can be simultaneously affected by some unobserved factors. Consequently, learning with only the labeled data may lead to severely biased results when deployed to the full population. Our paper tackles this challenge by exploiting the fact that in many applications the historical decisions were made by a set of heterogeneous decision-makers. In particular, we analyze this setup in a principled instrumental variable (IV) framework. We establish conditions for the full-population risk of any given prediction rule to be point-identified from the observed data and provide sharp risk bounds when the point identification fails. We further propose a weighted learning approach that learns prediction rules robust to the label selection bias in both identification settings. Finally, we apply our proposed approach to a semi-synthetic financial dataset and demonstrate its superior performance in the presence of selection bias.

Online Joint Assortment-Inventory Optimization under MNL Choices

We study an online joint assortment-inventory optimization problem, in which we assume that the choice behavior of each customer follows the Multinomial Logit (MNL) choice model, and the attraction parameters are unknown a priori. The retailer makes periodic assortment and inventory decisions to dynamically learn from the realized demands about the attraction parameters while maximizing the expected total profit over time. In this paper, we propose a novel algorithm that can effectively balance the exploration and exploitation in the online decision-making of assortment and inventory. Our algorithm builds on a new estimator for the MNL attraction parameters, a novel approach to incentivize exploration by adaptively tuning certain known and unknown parameters, and an optimization oracle to static single-cycle assortment-inventory planning problems with given parameters. We establish a regret upper bound for our algorithm and a lower bound for the online joint assortment-inventory optimization problem, suggesting that our algorithm achieves nearly optimal regret rate, provided that the static optimization oracle is exact. Then we incorporate more practical approximate static optimization oracles into our algorithm, and bound from above the impact of static optimization errors on the regret of our algorithm. At last, we perform numerical studies to demonstrate the effectiveness of our proposed algorithm.

Minimax Instrumental Variable Regression and $L_2$ Convergence Guarantees without Identification or Closedness

In this paper, we study nonparametric estimation of instrumental variable (IV) regressions. Recently, many flexible machine learning methods have been developed for instrumental variable estimation. However, these methods have at least one of the following limitations: (1) restricting the IV regression to be uniquely identified; (2) only obtaining estimation error rates in terms of pseudometrics (\emph{e.g.,} projected norm) rather than valid metrics (\emph{e.g.,} $L_2$ norm); or (3) imposing the so-called closedness condition that requires a certain conditional expectation operator to be sufficiently smooth. In this paper, we present the first method and analysis that can avoid all three limitations, while still permitting general function approximation. Specifically, we propose a new penalized minimax estimator that can converge to a fixed IV solution even when there are multiple solutions, and we derive a strong $L_2$ error rate for our estimator under lax conditions. Notably, this guarantee only needs a widely-used source condition and realizability assumptions, but not the so-called closedness condition. We argue that the source condition and the closedness condition are inherently conflicting, so relaxing the latter significantly improves upon the existing literature that requires both conditions. Our estimator can achieve this improvement because it builds on a novel formulation of the IV estimation problem as a constrained optimization problem.

Debiased Inference on Identified Linear Functionals of Underidentified Nuisances via Penalized Minimax Estimation

We study generic inference on identified linear functionals of nonunique nuisances defined as solutions to underidentified conditional moment restrictions. This problem appears in a variety of applications, including nonparametric instrumental variable models, proximal causal inference under unmeasured confounding, and missing-not-at-random data with shadow variables. Although the linear functionals of interest, such as average treatment effect, are identifiable under suitable conditions, nonuniqueness of nuisances pose serious challenges to statistical inference, since in this setting common nuisance estimators can be unstable and lack fixed limits. In this paper, we propose penalized minimax estimators for the nuisance functions and show they enable valid inference in this challenging setting. The proposed nuisance estimators can accommodate flexible function classes, and importantly, they can converge to fixed limits determined by the penalization, regardless of whether the nuisances are unique or not. We use the penalized nuisance estimators to form a debiased estimator for the linear functional of interest and prove its asymptotic normality under generic high-level conditions, which provide for asymptotically valid confidence intervals.

Doubly Robust Distributionally Robust Off-Policy Evaluation and Learning

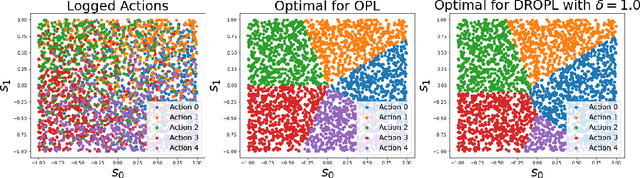
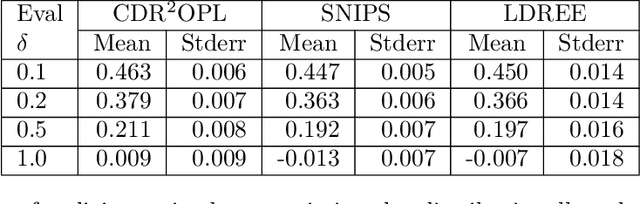
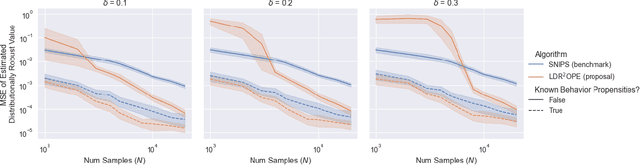
Off-policy evaluation and learning (OPE/L) use offline observational data to make better decisions, which is crucial in applications where experimentation is necessarily limited. OPE/L is nonetheless sensitive to discrepancies between the data-generating environment and that where policies are deployed. Recent work proposed distributionally robust OPE/L (DROPE/L) to remedy this, but the proposal relies on inverse-propensity weighting, whose regret rates may deteriorate if propensities are estimated and whose variance is suboptimal even if not. For vanilla OPE/L, this is solved by doubly robust (DR) methods, but they do not naturally extend to the more complex DROPE/L, which involves a worst-case expectation. In this paper, we propose the first DR algorithms for DROPE/L with KL-divergence uncertainty sets. For evaluation, we propose Localized Doubly Robust DROPE (LDR$^2$OPE) and prove its semiparametric efficiency under weak product rates conditions. Notably, thanks to a localization technique, LDR$^2$OPE only requires fitting a small number of regressions, just like DR methods for vanilla OPE. For learning, we propose Continuum Doubly Robust DROPL (CDR$^2$OPL) and show that, under a product rate condition involving a continuum of regressions, it enjoys a fast regret rate of $\mathcal{O}(N^{-1/2})$ even when unknown propensities are nonparametrically estimated. We further extend our results to general $f$-divergence uncertainty sets. We illustrate the advantage of our algorithms in simulations.

Long-term Causal Inference Under Persistent Confounding via Data Combination

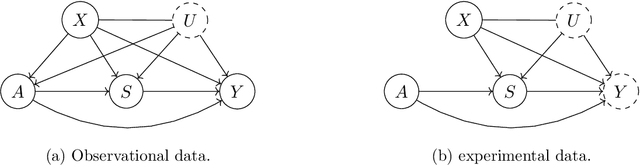
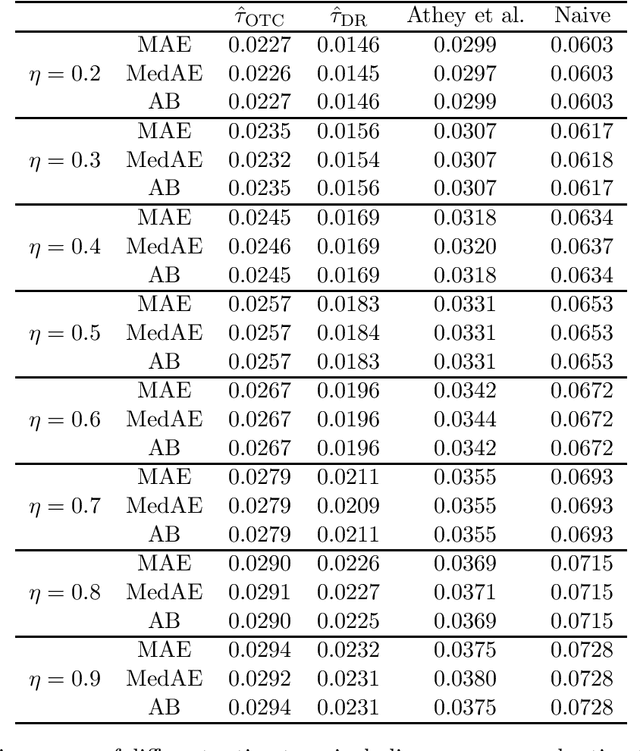
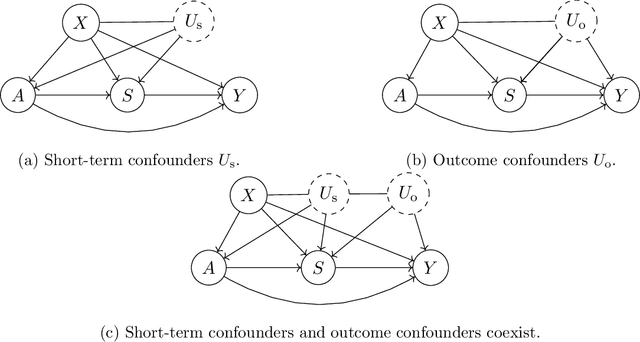
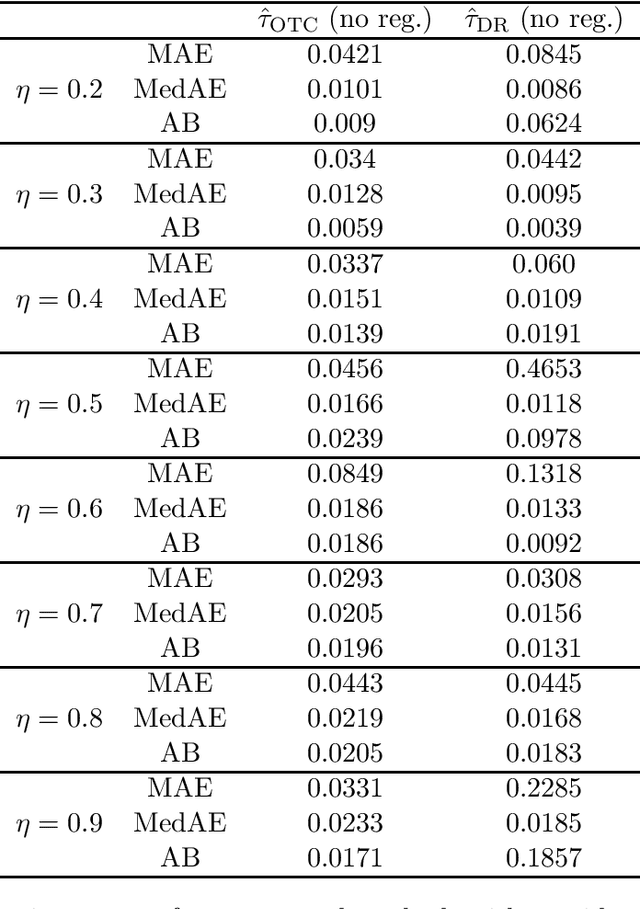
We study the identification and estimation of long-term treatment effects when both experimental and observational data are available. Since the long-term outcome is observed only after a long delay, it is not measured in the experimental data, but only recorded in the observational data. However, both types of data include observations of some short-term outcomes. In this paper, we uniquely tackle the challenge of persistent unmeasured confounders, i.e., some unmeasured confounders that can simultaneously affect the treatment, short-term outcomes and the long-term outcome, noting that they invalidate identification strategies in previous literature. To address this challenge, we exploit the sequential structure of multiple short-term outcomes, and develop three novel identification strategies for the average long-term treatment effect. We further propose three corresponding estimators and prove their asymptotic consistency and asymptotic normality. We finally apply our methods to estimate the effect of a job training program on long-term employment using semi-synthetic data. We numerically show that our proposals outperform existing methods that fail to handle persistent confounders.

Causal Inference Under Unmeasured Confounding With Negative Controls: A Minimax Learning Approach

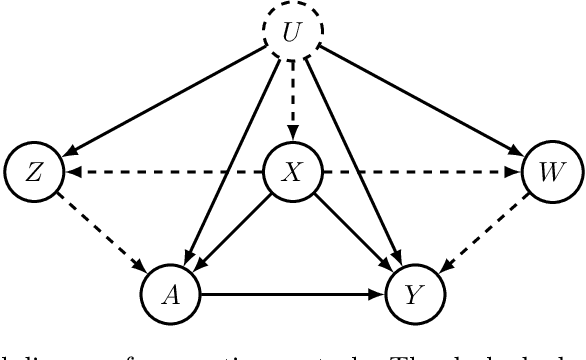
We study the estimation of causal parameters when not all confounders are observed and instead negative controls are available. Recent work has shown how these can enable identification and efficient estimation via two so-called bridge functions. In this paper, we tackle the primary challenge to causal inference using negative controls: the identification and estimation of these bridge functions. Previous work has relied on uniqueness and completeness assumptions on these functions that may be implausible in practice and also focused on their parametric estimation. Instead, we provide a new identification strategy that avoids both uniqueness and completeness. And, we provide a new estimators for these functions based on minimax learning formulations. These estimators accommodate general function classes such as reproducing Hilbert spaces and neural networks. We study finite-sample convergence results both for estimating bridge function themselves and for the final estimation of the causal parameter. We do this under a variety of combinations of assumptions that include realizability and closedness conditions on the hypothesis and critic classes employed in the minimax estimator. Depending on how much we are willing to assume, we obtain different convergence rates. In some cases, we show the estimate for the causal parameter may converge even when our bridge function estimators do not converge to any valid bridge function. And, in other cases, we show we can obtain semiparametric efficiency.

Fast Rates for Contextual Linear Optimization

Incorporating side observations of predictive features can help reduce uncertainty in operational decision making, but it also requires we tackle a potentially complex predictive relationship. Although one may use a variety of off-the-shelf machine learning methods to learn a predictive model and then plug it into our decision-making problem, a variety of recent work has instead advocated integrating estimation and optimization by taking into consideration downstream decision performance. Surprisingly, in the case of contextual linear optimization, we show that the naive plug-in approach actually achieves regret convergence rates that are significantly faster than the best-possible by methods that directly optimize down-stream decision performance. We show this by leveraging the fact that specific problem instances do not have arbitrarily bad near-degeneracy. While there are other pros and cons to consider as we discuss, our results highlight a very nuanced landscape for the enterprise to integrate estimation and optimization.