Gradient Methods with Online Scaling Part I. Theoretical Foundations

This paper establishes the theoretical foundations of the online scaled gradient methods (OSGM), a framework that utilizes online learning to adapt stepsizes and provably accelerate first-order methods. OSGM quantifies the effectiveness of a stepsize by a feedback function motivated from a convergence measure and uses the feedback to adjust the stepsize through an online learning algorithm. Consequently, instantiations of OSGM achieve convergence rates that are asymptotically no worse than the optimal stepsize. OSGM yields desirable convergence guarantees on smooth convex problems, including 1) trajectory-dependent global convergence on smooth convex objectives; 2) an improved complexity result on smooth strongly convex problems, and 3) local superlinear convergence. Notably, OSGM constitutes a new family of first-order methods with non-asymptotic superlinear convergence, joining the celebrated quasi-Newton methods. Finally, OSGM explains the empirical success of the popular hypergradient-descent heuristic in optimization for machine learning.

Adaptive Resolving Methods for Reinforcement Learning with Function Approximations

Reinforcement learning (RL) problems are fundamental in online decision-making and have been instrumental in finding an optimal policy for Markov decision processes (MDPs). Function approximations are usually deployed to handle large or infinite state-action space. In our work, we consider the RL problems with function approximation and we develop a new algorithm to solve it efficiently. Our algorithm is based on the linear programming (LP) reformulation and it resolves the LP at each iteration improved with new data arrival. Such a resolving scheme enables our algorithm to achieve an instance-dependent sample complexity guarantee, more precisely, when we have $N$ data, the output of our algorithm enjoys an instance-dependent $\tilde{O}(1/N)$ suboptimality gap. In comparison to the $O(1/\sqrt{N})$ worst-case guarantee established in the previous literature, our instance-dependent guarantee is tighter when the underlying instance is favorable, and the numerical experiments also reveal the efficient empirical performances of our algorithms.

Solver-Informed RL: Grounding Large Language Models for Authentic Optimization Modeling

Optimization modeling is fundamental to decision-making across diverse domains.Despite progress in automating optimization formulation from natural language descriptions, Large Language Models (LLMs) often struggle to generate formally correct and usable models due to hallucinations, posing a challenge for reliable automation. Inspired by the success of Reinforcement Learning (RL) in enhancing Large Reasoning Models, we present Solver-Informed Reinforcement Learning (SIRL).This novel framework leverages external optimization solvers as verifiable reward mechanisms to significantly improve the authenticity of LLMs for optimization modeling.Acting as precise verifiers, these solvers automatically assess the executable code and the instance-level mathematical model represented by the associated LP file, yielding precise and comprehensive feedback signals -- including syntax, feasibility, and solution quality that directly inform the RL process. This automated verification process, powered by classic optimization solvers, also underpins our instance-enhanced self-consistency method to synthesize high-quality training data. Extensive experiments on diverse public benchmarks demonstrate that SIRL achieves state-of-the-art performance, substantially outperforming existing methods in generating accurate and executable optimization models.

Beyond $\mathcal{O}(\sqrt{T})$ Regret: Decoupling Learning and Decision-making in Online Linear Programming

Online linear programming plays an important role in both revenue management and resource allocation, and recent research has focused on developing efficient first-order online learning algorithms. Despite the empirical success of first-order methods, they typically achieve a regret no better than $\mathcal{O} ( \sqrt{T} )$, which is suboptimal compared to the $\mathcal{O} (\log T)$ bound guaranteed by the state-of-the-art linear programming (LP)-based online algorithms. This paper establishes a general framework that improves upon the $\mathcal{O} ( \sqrt{T} )$ result when the LP dual problem exhibits certain error bound conditions. For the first time, we show that first-order learning algorithms achieve $o( \sqrt{T} )$ regret in the continuous support setting and $\mathcal{O} (\log T)$ regret in the finite support setting beyond the non-degeneracy assumption. Our results significantly improve the state-of-the-art regret results and provide new insights for sequential decision-making.

Wait-Less Offline Tuning and Re-solving for Online Decision Making

Online linear programming (OLP) has found broad applications in revenue management and resource allocation. State-of-the-art OLP algorithms achieve low regret by repeatedly solving linear programming (LP) subproblems that incorporate updated resource information. However, LP-based methods are computationally expensive and often inefficient for large-scale applications. In contrast, recent first-order OLP algorithms are more computationally efficient but typically suffer from worse regret guarantees. To address these shortcomings, we propose a new algorithm that combines the strengths of LP-based and first-order OLP methods. The algorithm re-solves the LP subproblems periodically at a predefined frequency $f$ and uses the latest dual prices to guide online decision-making. In addition, a first-order method runs in parallel during each interval between LP re-solves, smoothing resource consumption. Our algorithm achieves $\mathscr{O}(\log (T/f) + \sqrt{f})$ regret, delivering a "wait-less" online decision-making process that balances the computational efficiency of first-order methods and the superior regret guarantee of LP-based methods.

Gradient Methods with Online Scaling

We introduce a framework to accelerate the convergence of gradient-based methods with online learning. The framework learns to scale the gradient at each iteration through an online learning algorithm and provably accelerates gradient-based methods asymptotically. In contrast with previous literature, where convergence is established based on worst-case analysis, our framework provides a strong convergence guarantee with respect to the optimal scaling matrix for the iteration trajectory. For smooth strongly convex optimization, our results provide an $O(\kappa^\star \log(1/\varepsilon)$) complexity result, where $\kappa^\star$ is the condition number achievable by the optimal preconditioner, improving on the previous $O(\sqrt{n}\kappa^\star \log(1/\varepsilon))$ result. In particular, a variant of our method achieves superlinear convergence on convex quadratics. For smooth convex optimization, we show for the first time that the widely-used hypergradient descent heuristic improves on the convergence of gradient descent.

A Robust Anchor-based Method for Multi-Camera Pedestrian Localization

This paper addresses the problem of vision-based pedestrian localization, which estimates a pedestrian's location using images and camera parameters. In practice, however, calibrated camera parameters often deviate from the ground truth, leading to inaccuracies in localization. To address this issue, we propose an anchor-based method that leverages fixed-position anchors to reduce the impact of camera parameter errors. We provide a theoretical analysis that demonstrates the robustness of our approach. Experiments conducted on simulated, real-world, and public datasets show that our method significantly improves localization accuracy and remains resilient to noise in camera parameters, compared to methods without anchors.

Online Linear Programming with Batching

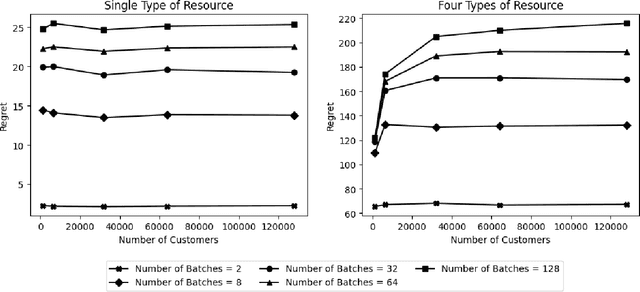
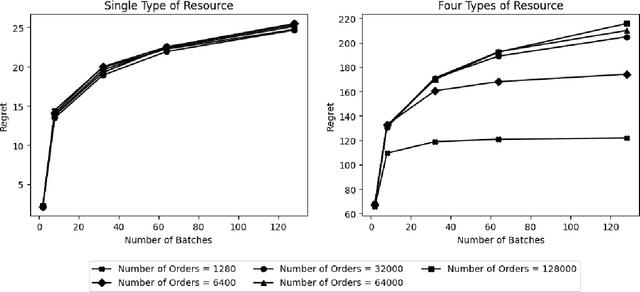
We study Online Linear Programming (OLP) with batching. The planning horizon is cut into $K$ batches, and the decisions on customers arriving within a batch can be delayed to the end of their associated batch. Compared with OLP without batching, the ability to delay decisions brings better operational performance, as measured by regret. Two research questions of interest are: (1) What is a lower bound of the regret as a function of $K$? (2) What algorithms can achieve the regret lower bound? These questions have been analyzed in the literature when the distribution of the reward and the resource consumption of the customers have finite support. By contrast, this paper analyzes these questions when the conditional distribution of the reward given the resource consumption is continuous, and we show the answers are different under this setting. When there is only a single type of resource and the decision maker knows the total number of customers, we propose an algorithm with a $O(\log K)$ regret upper bound and provide a $\Omega(\log K)$ regret lower bound. We also propose algorithms with $O(\log K)$ regret upper bound for the setting in which there are multiple types of resource and the setting in which customers arrive following a Poisson process. All these regret upper and lower bounds are independent of the length of the planning horizon, and all the proposed algorithms delay decisions on customers arriving in only the first and the last batch. We also take customer impatience into consideration and establish a way of selecting an appropriate batch size.

Adam-mini: Use Fewer Learning Rates To Gain More

We propose Adam-mini, an optimizer that achieves on-par or better performance than AdamW with 45% to 50% less memory footprint. Adam-mini reduces memory by cutting down the learning rate resources in Adam (i.e., $1/\sqrt{v}$). We find that $\geq$ 90% of these learning rates in $v$ could be harmlessly removed if we (1) carefully partition the parameters into blocks following our proposed principle on Hessian structure; (2) assign a single but good learning rate to each parameter block. We further find that, for each of these parameter blocks, there exists a single high-quality learning rate that can outperform Adam, provided that sufficient resources are available to search it out. We then provide one cost-effective way to find good learning rates and propose Adam-mini. Empirically, we verify that Adam-mini performs on par or better than AdamW on various language models sized from 125M to 7B for pre-training, supervised fine-tuning, and RLHF. The reduced memory footprint of Adam-mini also alleviates communication overheads among GPUs and CPUs, thereby increasing throughput. For instance, Adam-mini achieves 49.6% higher throughput than AdamW when pre-training Llama2-7B on $2\times$ A800-80GB GPUs, which saves 33% wall-clock time for pre-training.

Diffusion Model for Data-Driven Black-Box Optimization

Generative AI has redefined artificial intelligence, enabling the creation of innovative content and customized solutions that drive business practices into a new era of efficiency and creativity. In this paper, we focus on diffusion models, a powerful generative AI technology, and investigate their potential for black-box optimization over complex structured variables. Consider the practical scenario where one wants to optimize some structured design in a high-dimensional space, based on massive unlabeled data (representing design variables) and a small labeled dataset. We study two practical types of labels: 1) noisy measurements of a real-valued reward function and 2) human preference based on pairwise comparisons. The goal is to generate new designs that are near-optimal and preserve the designed latent structures. Our proposed method reformulates the design optimization problem into a conditional sampling problem, which allows us to leverage the power of diffusion models for modeling complex distributions. In particular, we propose a reward-directed conditional diffusion model, to be trained on the mixed data, for sampling a near-optimal solution conditioned on high predicted rewards. Theoretically, we establish sub-optimality error bounds for the generated designs. The sub-optimality gap nearly matches the optimal guarantee in off-policy bandits, demonstrating the efficiency of reward-directed diffusion models for black-box optimization. Moreover, when the data admits a low-dimensional latent subspace structure, our model efficiently generates high-fidelity designs that closely respect the latent structure. We provide empirical experiments validating our model in decision-making and content-creation tasks.