OR-R1: Automating Modeling and Solving of Operations Research Optimization Problem via Test-Time Reinforcement Learning

Optimization modeling and solving are fundamental to the application of Operations Research (OR) in real-world decision making, yet the process of translating natural language problem descriptions into formal models and solver code remains highly expertise intensive. While recent advances in large language models (LLMs) have opened new opportunities for automation, the generalization ability and data efficiency of existing LLM-based methods are still limited, asmost require vast amounts of annotated or synthetic data, resulting in high costs and scalability barriers. In this work, we present OR-R1, a data-efficient training framework for automated optimization modeling and solving. OR-R1 first employs supervised fine-tuning (SFT) to help the model acquire the essential reasoning patterns for problem formulation and code generation from limited labeled data. In addition, it improves the capability and consistency through Test-Time Group Relative Policy Optimization (TGRPO). This two-stage design enables OR-R1 to leverage both scarce labeled and abundant unlabeled data for effective learning. Experiments show that OR-R1 achieves state-of-the-art performance with an average solving accuracy of $67.7\%$, using only $1/10$ the synthetic data required by prior methods such as ORLM, exceeding ORLM's solving accuracy by up to $4.2\%$. Remarkably, OR-R1 outperforms ORLM by over $2.4\%$ with just $100$ synthetic samples. Furthermore, TGRPO contributes an additional $3.1\%-6.4\%$ improvement in accuracy, significantly narrowing the gap between single-attempt (Pass@1) and multi-attempt (Pass@8) performance from $13\%$ to $7\%$. Extensive evaluations across diverse real-world benchmarks demonstrate that OR-R1 provides a robust, scalable, and cost-effective solution for automated OR optimization problem modeling and solving, lowering the expertise and data barriers for industrial OR applications.

Make Optimization Once and for All with Fine-grained Guidance

Learning to Optimize (L2O) enhances optimization efficiency with integrated neural networks. L2O paradigms achieve great outcomes, e.g., refitting optimizer, generating unseen solutions iteratively or directly. However, conventional L2O methods require intricate design and rely on specific optimization processes, limiting scalability and generalization. Our analyses explore general framework for learning optimization, called Diff-L2O, focusing on augmenting sampled solutions from a wider view rather than local updates in real optimization process only. Meanwhile, we give the related generalization bound, showing that the sample diversity of Diff-L2O brings better performance. This bound can be simply applied to other fields, discussing diversity, mean-variance, and different tasks. Diff-L2O's strong compatibility is empirically verified with only minute-level training, comparing with other hour-levels.

Parameter-Adaptive Dynamic Pricing

Dynamic pricing is crucial in sectors like e-commerce and transportation, balancing exploration of demand patterns and exploitation of pricing strategies. Existing methods often require precise knowledge of the demand function, e.g., the H{\"o}lder smoothness level and Lipschitz constant, limiting practical utility. This paper introduces an adaptive approach to address these challenges without prior parameter knowledge. By partitioning the demand function's domain and employing a linear bandit structure, we develop an algorithm that manages regret efficiently, enhancing flexibility and practicality. Our Parameter-Adaptive Dynamic Pricing (PADP) algorithm outperforms existing methods, offering improved regret bounds and extensions for contextual information. Numerical experiments validate our approach, demonstrating its superiority in handling unknown demand parameters.

Minimax Optimality in Contextual Dynamic Pricing with General Valuation Models

Dynamic pricing, the practice of adjusting prices based on contextual factors, has gained significant attention due to its impact on revenue maximization. In this paper, we address the contextual dynamic pricing problem, which involves pricing decisions based on observable product features and customer characteristics. We propose a novel algorithm that achieves improved regret bounds while minimizing assumptions about the problem. Our algorithm discretizes the unknown noise distribution and combines the upper confidence bounds with a layered data partitioning technique to effectively regulate regret in each episode. These techniques effectively control the regret associated with pricing decisions, leading to the minimax optimality. Specifically, our algorithm achieves a regret upper bound of $\tilde{\mathcal{O}}(\rho_{\mathcal{V}}^{\frac{1}{3}}(\delta) T^{\frac{2}{3}})$, where $\rho_{\mathcal{V}}(\delta)$ represents the estimation error of the valuation function. Importantly, this bound matches the lower bound up to logarithmic terms, demonstrating the minimax optimality of our approach. Furthermore, our method extends beyond linear valuation models commonly used in dynamic pricing by considering general function spaces. We simplify the estimation process by reducing it to general offline regression oracles, making implementation more straightforward.

RL in Markov Games with Independent Function Approximation: Improved Sample Complexity Bound under the Local Access Model

Efficiently learning equilibria with large state and action spaces in general-sum Markov games while overcoming the curse of multi-agency is a challenging problem. Recent works have attempted to solve this problem by employing independent linear function classes to approximate the marginal $Q$-value for each agent. However, existing sample complexity bounds under such a framework have a suboptimal dependency on the desired accuracy $\varepsilon$ or the action space. In this work, we introduce a new algorithm, Lin-Confident-FTRL, for learning coarse correlated equilibria (CCE) with local access to the simulator, i.e., one can interact with the underlying environment on the visited states. Up to a logarithmic dependence on the size of the state space, Lin-Confident-FTRL learns $\epsilon$-CCE with a provable optimal accuracy bound $O(\epsilon^{-2})$ and gets rids of the linear dependency on the action space, while scaling polynomially with relevant problem parameters (such as the number of agents and time horizon). Moreover, our analysis of Linear-Confident-FTRL generalizes the virtual policy iteration technique in the single-agent local planning literature, which yields a new computationally efficient algorithm with a tighter sample complexity bound when assuming random access to the simulator.

Stochastic Graph Bandit Learning with Side-Observations

In this paper, we investigate the stochastic contextual bandit with general function space and graph feedback. We propose an algorithm that addresses this problem by adapting to both the underlying graph structures and reward gaps. To the best of our knowledge, our algorithm is the first to provide a gap-dependent upper bound in this stochastic setting, bridging the research gap left by the work in [35]. In comparison to [31,33,35], our method offers improved regret upper bounds and does not require knowledge of graphical quantities. We conduct numerical experiments to demonstrate the computational efficiency and effectiveness of our approach in terms of regret upper bounds. These findings highlight the significance of our algorithm in advancing the field of stochastic contextual bandits with graph feedback, opening up avenues for practical applications in various domains.

Provably Efficient Learning in Partially Observable Contextual Bandit

In this paper, we investigate transfer learning in partially observable contextual bandits, where agents have limited knowledge from other agents and partial information about hidden confounders. We first convert the problem to identifying or partially identifying causal effects between actions and rewards through optimization problems. To solve these optimization problems, we discretize the original functional constraints of unknown distributions into linear constraints, and sample compatible causal models via sequentially solving linear programmings to obtain causal bounds with the consideration of estimation error. Our sampling algorithms provide desirable convergence results for suitable sampling distributions. We then show how causal bounds can be applied to improving classical bandit algorithms and affect the regrets with respect to the size of action sets and function spaces. Notably, in the task with function approximation which allows us to handle general context distributions, our method improves the order dependence on function space size compared with previous literatures. We formally prove that our causally enhanced algorithms outperform classical bandit algorithms and achieve orders of magnitude faster convergence rates. Finally, we perform simulations that demonstrate the efficiency of our strategy compared to the current state-of-the-art methods. This research has the potential to enhance the performance of contextual bandit agents in real-world applications where data is scarce and costly to obtain.

Debiasing Recommendation by Learning Identifiable Latent Confounders

Recommendation systems aim to predict users' feedback on items not exposed to them. Confounding bias arises due to the presence of unmeasured variables (e.g., the socio-economic status of a user) that can affect both a user's exposure and feedback. Existing methods either (1) make untenable assumptions about these unmeasured variables or (2) directly infer latent confounders from users' exposure. However, they cannot guarantee the identification of counterfactual feedback, which can lead to biased predictions. In this work, we propose a novel method, i.e., identifiable deconfounder (iDCF), which leverages a set of proxy variables (e.g., observed user features) to resolve the aforementioned non-identification issue. The proposed iDCF is a general deconfounded recommendation framework that applies proximal causal inference to infer the unmeasured confounders and identify the counterfactual feedback with theoretical guarantees. Extensive experiments on various real-world and synthetic datasets verify the proposed method's effectiveness and robustness.

Single-Trajectory Distributionally Robust Reinforcement Learning

As a framework for sequential decision-making, Reinforcement Learning (RL) has been regarded as an essential component leading to Artificial General Intelligence (AGI). However, RL is often criticized for having the same training environment as the test one, which also hinders its application in the real world. To mitigate this problem, Distributionally Robust RL (DRRL) is proposed to improve the worst performance in a set of environments that may contain the unknown test environment. Due to the nonlinearity of the robustness goal, most of the previous work resort to the model-based approach, learning with either an empirical distribution learned from the data or a simulator that can be sampled infinitely, which limits their applications in simple dynamics environments. In contrast, we attempt to design a DRRL algorithm that can be trained along a single trajectory, i.e., no repeated sampling from a state. Based on the standard Q-learning, we propose distributionally robust Q-learning with the single trajectory (DRQ) and its average-reward variant named differential DRQ. We provide asymptotic convergence guarantees and experiments for both settings, demonstrating their superiority in the perturbed environments against the non-robust ones.

Distributionally Robust Offline Reinforcement Learning with Linear Function Approximation

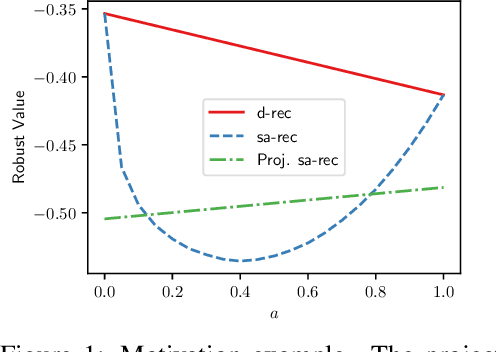
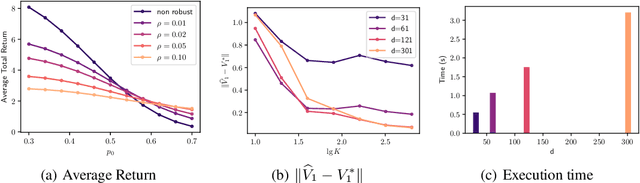
Among the reasons hindering reinforcement learning (RL) applications to real-world problems, two factors are critical: limited data and the mismatch between the testing environment (real environment in which the policy is deployed) and the training environment (e.g., a simulator). This paper attempts to address these issues simultaneously with distributionally robust offline RL, where we learn a distributionally robust policy using historical data obtained from the source environment by optimizing against a worst-case perturbation thereof. In particular, we move beyond tabular settings and consider linear function approximation. More specifically, we consider two settings, one where the dataset is well-explored and the other where the dataset has sufficient coverage. We propose two algorithms -- one for each of the two settings -- that achieve error bounds $\tilde{O}(d^{1/2}/N^{1/2})$ and $\tilde{O}(d^{3/2}/N^{1/2})$ respectively, where $d$ is the dimension in the linear function approximation and $N$ is the number of trajectories in the dataset. To the best of our knowledge, they provide the first non-asymptotic results of the sample complexity in this setting. Diverse experiments are conducted to demonstrate our theoretical findings, showing the superiority of our algorithm against the non-robust one.