Learning to Help in Multi-Class Settings

Deploying complex machine learning models on resource-constrained devices is challenging due to limited computational power, memory, and model retrainability. To address these limitations, a hybrid system can be established by augmenting the local model with a server-side model, where samples are selectively deferred by a rejector and then sent to the server for processing. The hybrid system enables efficient use of computational resources while minimizing the overhead associated with server usage. The recently proposed Learning to Help (L2H) model trains a server model given a fixed local (client) model, differing from the Learning to Defer (L2D) framework, which trains the client for a fixed (expert) server. In both L2D and L2H, the training includes learning a rejector at the client to determine when to query the server. In this work, we extend the L2H model from binary to multi-class classification problems and demonstrate its applicability in a number of different scenarios of practical interest in which access to the server may be limited by cost, availability, or policy. We derive a stage-switching surrogate loss function that is differentiable, convex, and consistent with the Bayes rule corresponding to the 0-1 loss for the L2H model. Experiments show that our proposed methods offer an efficient and practical solution for multi-class classification in resource-constrained environments.

Differentially Private Distribution Estimation Using Functional Approximation

The cumulative distribution function (CDF) is fundamental due to its ability to reveal information about random variables, making it essential in studies that require privacy-preserving methods to protect sensitive data. This paper introduces a novel privacy-preserving CDF method inspired by the functional analysis and functional mechanism. Our approach projects the empirical CDF into a predefined space, approximating it using specific functions, and protects the coefficients to achieve a differentially private empirical CDF. Compared to existing methods like histogram queries and adaptive quantiles, our method is preferable in decentralized settings and scenarios where CDFs must be updated with newly collected data.

Understanding Generative AI Content with Embedding Models

The construction of high-quality numerical features is critical to any quantitative data analysis. Feature engineering has been historically addressed by carefully hand-crafting data representations based on domain expertise. This work views the internal representations of modern deep neural networks (DNNs), called embeddings, as an automated form of traditional feature engineering. For trained DNNs, we show that these embeddings can reveal interpretable, high-level concepts in unstructured sample data. We use these embeddings in natural language and computer vision tasks to uncover both inherent heterogeneity in the underlying data and human-understandable explanations for it. In particular, we find empirical evidence that there is inherent separability between real data and that generated from AI models.

Measuring model variability using robust non-parametric testing

Training a deep neural network often involves stochastic optimization, meaning each run will produce a different model. The seed used to initialize random elements of the optimization procedure heavily influences the quality of a trained model, which may be obscure from many commonly reported summary statistics, like accuracy. However, random seed is often not included in hyper-parameter optimization, perhaps because the relationship between seed and model quality is hard to describe. This work attempts to describe the relationship between deep net models trained with different random seeds and the behavior of the expected model. We adopt robust hypothesis testing to propose a novel summary statistic for network similarity, referred to as the $\alpha$-trimming level. We use the $\alpha$-trimming level to show that the empirical cumulative distribution function of an ensemble model created from a collection of trained models with different random seeds approximates the average of these functions as the number of models in the collection grows large. This insight provides guidance for how many random seeds should be sampled to ensure that an ensemble of these trained models is a reliable representative. We also show that the $\alpha$-trimming level is more expressive than different performance metrics like validation accuracy, churn, or expected calibration error when taken alone and may help with random seed selection in a more principled fashion. We demonstrate the value of the proposed statistic in real experiments and illustrate the advantage of fine-tuning over random seed with an experiment in transfer learning.

Robust Nonparametric Hypothesis Testing to Understand Variability in Training Neural Networks

Training a deep neural network (DNN) often involves stochastic optimization, which means each run will produce a different model. Several works suggest this variability is negligible when models have the same performance, which in the case of classification is test accuracy. However, models with similar test accuracy may not be computing the same function. We propose a new measure of closeness between classification models based on the output of the network before thresholding. Our measure is based on a robust hypothesis-testing framework and can be adapted to other quantities derived from trained models.

Structured Low-Rank Tensors for Generalized Linear Models

Recent works have shown that imposing tensor structures on the coefficient tensor in regression problems can lead to more reliable parameter estimation and lower sample complexity compared to vector-based methods. This work investigates a new low-rank tensor model, called Low Separation Rank (LSR), in Generalized Linear Model (GLM) problems. The LSR model -- which generalizes the well-known Tucker and CANDECOMP/PARAFAC (CP) models, and is a special case of the Block Tensor Decomposition (BTD) model -- is imposed onto the coefficient tensor in the GLM model. This work proposes a block coordinate descent algorithm for parameter estimation in LSR-structured tensor GLMs. Most importantly, it derives a minimax lower bound on the error threshold on estimating the coefficient tensor in LSR tensor GLM problems. The minimax bound is proportional to the intrinsic degrees of freedom in the LSR tensor GLM problem, suggesting that its sample complexity may be significantly lower than that of vectorized GLMs. This result can also be specialised to lower bound the estimation error in CP and Tucker-structured GLMs. The derived bounds are comparable to tight bounds in the literature for Tucker linear regression, and the tightness of the minimax lower bound is further assessed numerically. Finally, numerical experiments on synthetic datasets demonstrate the efficacy of the proposed LSR tensor model for three regression types (linear, logistic and Poisson). Experiments on a collection of medical imaging datasets demonstrate the usefulness of the LSR model over other tensor models (Tucker and CP) on real, imbalanced data with limited available samples.

TorchNTK: A Library for Calculation of Neural Tangent Kernels of PyTorch Models

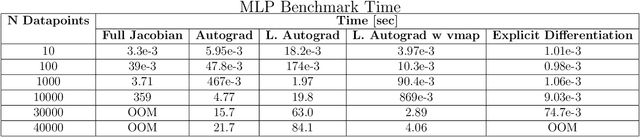
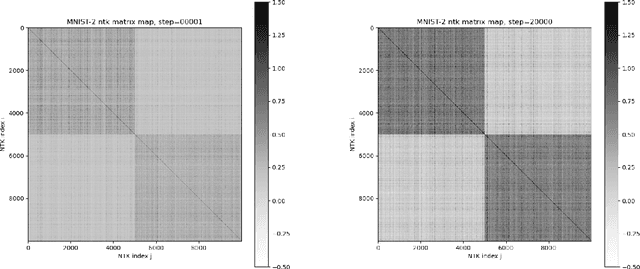
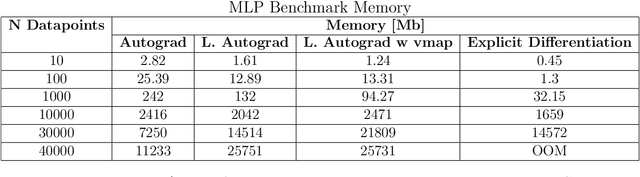
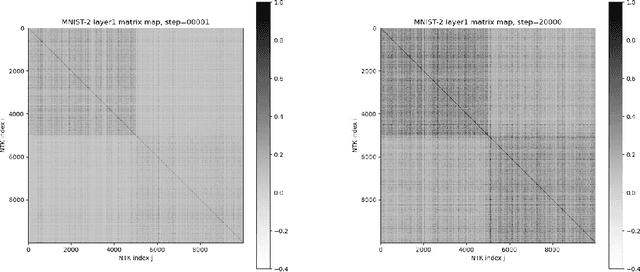
We introduce torchNTK, a python library to calculate the empirical neural tangent kernel (NTK) of neural network models in the PyTorch framework. We provide an efficient method to calculate the NTK of multilayer perceptrons. We compare the explicit differentiation implementation against autodifferentiation implementations, which have the benefit of extending the utility of the library to any architecture supported by PyTorch, such as convolutional networks. A feature of the library is that we expose the user to layerwise NTK components, and show that in some regimes a layerwise calculation is more memory efficient. We conduct preliminary experiments to demonstrate use cases for the software and probe the NTK.

Low-Rank Phase Retrieval with Structured Tensor Models

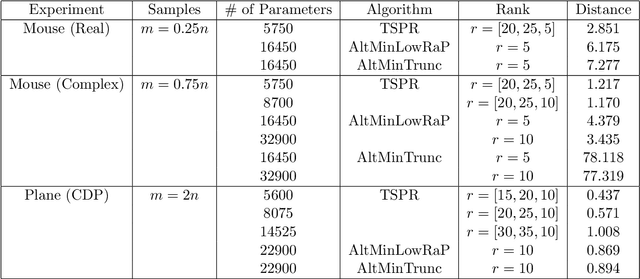
We study the low-rank phase retrieval problem, where the objective is to recover a sequence of signals (typically images) given the magnitude of linear measurements of those signals. Existing solutions involve recovering a matrix constructed by vectorizing and stacking each image. These algorithms model this matrix to be low-rank and leverage the low-rank property to decrease the sample complexity required for accurate recovery. However, when the number of available measurements is more limited, these low-rank matrix models can often fail. We propose an algorithm called Tucker-Structured Phase Retrieval (TSPR) that models the sequence of images as a tensor rather than a matrix that we factorize using the Tucker decomposition. This factorization reduces the number of parameters that need to be estimated, allowing for a more accurate reconstruction in the under-sampled regime. Interestingly, we observe that this structure also has improved performance in the over-determined setting when the Tucker ranks are chosen appropriately. We demonstrate the effectiveness of our approach on real video datasets under several different measurement models.

Network Traffic Shaping for Enhancing Privacy in IoT Systems

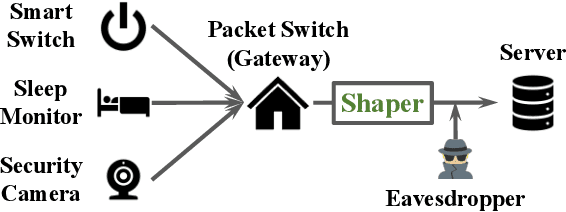
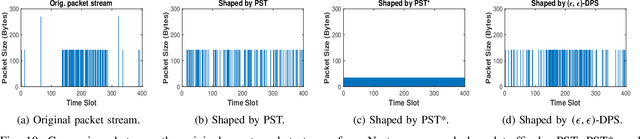
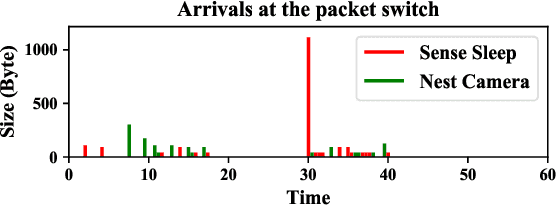
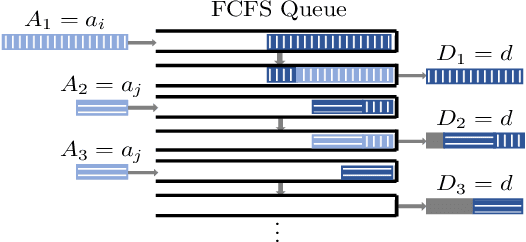
Motivated by privacy issues caused by inference attacks on user activities in the packet sizes and timing information of Internet of Things (IoT) network traffic, we establish a rigorous event-level differential privacy (DP) model on infinite packet streams. We propose a memoryless traffic shaping mechanism satisfying a first-come-first-served queuing discipline that outputs traffic dependent on the input using a DP mechanism. We show that in special cases the proposed mechanism recovers existing shapers which standardize the output independently from the input. To find the optimal shapers for given levels of privacy and transmission efficiency, we formulate the constrained problem of minimizing the expected delay per packet and propose using the expected queue size across time as a proxy. We further show that the constrained minimization is a convex program. We demonstrate the effect of shapers on both synthetic data and packet traces from actual IoT devices. The experimental results reveal inherent privacy-overhead tradeoffs: more shaping overhead provides better privacy protection. Under the same privacy level, there naturally exists a tradeoff between dummy traffic and delay. When dealing with heavier or less bursty input traffic, all shapers become more overhead-efficient. We also show that increased traffic from a larger number of IoT devices makes guaranteeing event-level privacy easier. The DP shaper offers tunable privacy that is invariant with the change in the input traffic distribution and has an advantage in handling burstiness over traffic-independent shapers. This approach well accommodates heterogeneous network conditions and enables users to adapt to their privacy/overhead demands.

A Minimax Lower Bound for Low-Rank Matrix-Variate Logistic Regression

This paper considers the problem of matrix-variate logistic regression. The fundamental error threshold on estimating coefficient matrices in the logistic regression problem is found by deriving a lower bound on the minimax risk. The focus of this paper is on derivation of a minimax risk lower bound for low-rank coefficient matrices. The bound depends explicitly on the dimensions and distribution of the covariates, the rank and energy of the coefficient matrix, and the number of samples. The resulting bound is proportional to the intrinsic degrees of freedom in the problem, which suggests the sample complexity of the low-rank matrix logistic regression problem can be lower than that for vectorized logistic regression. \color{red}\color{black} The proof techniques utilized in this work also set the stage for development of minimax lower bounds for tensor-variate logistic regression problems.