EditBoard: Towards A Comprehensive Evaluation Benchmark for Text-based Video Editing Models

The rapid development of diffusion models has significantly advanced AI-generated content (AIGC), particularly in Text-to-Image (T2I) and Text-to-Video (T2V) generation. Text-based video editing, leveraging these generative capabilities, has emerged as a promising field, enabling precise modifications to videos based on text prompts. Despite the proliferation of innovative video editing models, there is a conspicuous lack of comprehensive evaluation benchmarks that holistically assess these models' performance across various dimensions. Existing evaluations are limited and inconsistent, typically summarizing overall performance with a single score, which obscures models' effectiveness on individual editing tasks. To address this gap, we propose EditBoard, the first comprehensive evaluation benchmark for text-based video editing models. EditBoard encompasses nine automatic metrics across four dimensions, evaluating models on four task categories and introducing three new metrics to assess fidelity. This task-oriented benchmark facilitates objective evaluation by detailing model performance and providing insights into each model's strengths and weaknesses. By open-sourcing EditBoard, we aim to standardize evaluation and advance the development of robust video editing models.

MoFO: Momentum-Filtered Optimizer for Mitigating Forgetting in LLM Fine-Tuning

Recently, large language models (LLMs) have demonstrated remarkable capabilities in a wide range of tasks. Typically, an LLM is pre-trained on large corpora and subsequently fine-tuned on task-specific datasets. However, during fine-tuning, LLMs may forget the knowledge acquired in the pre-training stage, leading to a decline in general capabilities. To address this issue, we propose a new fine-tuning algorithm termed Momentum-Filtered Optimizer (MoFO). The key idea of MoFO is to iteratively select and update the model parameters with the largest momentum magnitudes. Compared to full-parameter training, MoFO achieves similar fine-tuning performance while keeping parameters closer to the pre-trained model, thereby mitigating knowledge forgetting. Unlike most existing methods for forgetting mitigation, MoFO combines the following two advantages. First, MoFO does not require access to pre-training data. This makes MoFO particularly suitable for fine-tuning scenarios where pre-training data is unavailable, such as fine-tuning checkpoint-only open-source LLMs. Second, MoFO does not alter the original loss function. This could avoid impairing the model performance on the fine-tuning tasks. We validate MoFO through rigorous convergence analysis and extensive experiments, demonstrating its superiority over existing methods in mitigating forgetting and enhancing fine-tuning performance.

PDHG-Unrolled Learning-to-Optimize Method for Large-Scale Linear Programming

Solving large-scale linear programming (LP) problems is an important task in various areas such as communication networks, power systems, finance and logistics. Recently, two distinct approaches have emerged to expedite LP solving: (i) First-order methods (FOMs); (ii) Learning to optimize (L2O). In this work, we propose an FOM-unrolled neural network (NN) called PDHG-Net, and propose a two-stage L2O method to solve large-scale LP problems. The new architecture PDHG-Net is designed by unrolling the recently emerged PDHG method into a neural network, combined with channel-expansion techniques borrowed from graph neural networks. We prove that the proposed PDHG-Net can recover PDHG algorithm, thus can approximate optimal solutions of LP instances with a polynomial number of neurons. We propose a two-stage inference approach: first use PDHG-Net to generate an approximate solution, and then apply PDHG algorithm to further improve the solution. Experiments show that our approach can significantly accelerate LP solving, achieving up to a 3$\times$ speedup compared to FOMs for large-scale LP problems.

Ultraviolet Scattering Communication Using Subcarrier Intensity Modulation over Atmospheric Turbulence Channels

A closed-form non-line-of-sight (NLOS) turbulenceinduced fluctuation model is derived for ultraviolet scattering communication (USC), which models the received irradiance fluctuation by Meijer G function. Based on this model, we investigate the error rates of the USC system in NLOS case using different modulation techniques. Closed-form error rate results are derived by integration of Meijer G function. Inspired by the decomposition of different turbulence parameters, we use a series expansion of hypergeometric function and obtain the error rate expressions by the sum of four infinite series. The numerical results show that our error rate results are accurate in NLOS case. We also study the relationship between the turbulence influence and NLOS transceiver configurations. The numerical results show that when two-LOS link formulates the same distance, the turbulence influence is the strongest for long ranges and the weakest for short ranges.

An Unbiased Symmetric Matrix Estimator for Topology Inference under Partial Observability

Network topology inference is a fundamental problem in many applications of network science, such as locating the source of fake news, brain connectivity networks detection, etc. Many real-world situations suffer from a critical problem that only a limited part of observations are available. This letter considers the problem of network topology inference under the framework of partial observability. Based on the vector autoregressive model, we propose a novel unbiased estimator for the symmetric network topology with the Gaussian noise and the Laplacian combination rule. Theoretically, we prove that it converges to the network combination matrix in probability. Furthermore, by utilizing the Gaussian mixture model algorithm, an effective algorithm called network inference Gauss algorithm is developed to infer the network structure. Finally, compared with the state-of-the-art methods, numerical experiments demonstrate the proposed algorithm enjoys better performance in the case of small sample sizes.

Attention Cube Network for Image Restoration

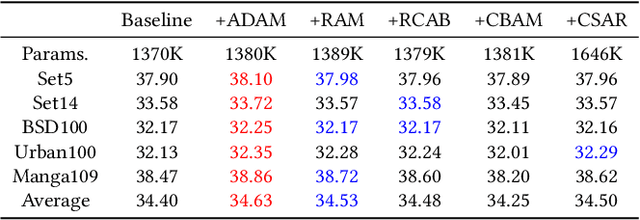
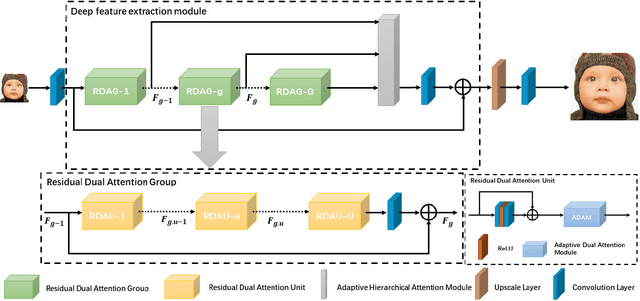
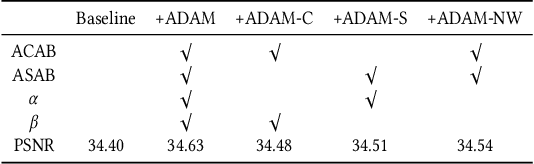
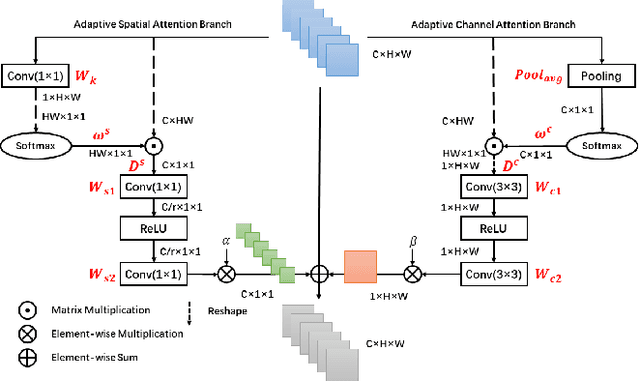
Recently, deep convolutional neural network (CNN) have been widely used in image restoration and obtained great success. However, most of existing methods are limited to local receptive field and equal treatment of different types of information. Besides, existing methods always use a multi-supervised method to aggregate different feature maps, which can not effectively aggregate hierarchical feature information. To address these issues, we propose an attention cube network (A-CubeNet) for image restoration for more powerful feature expression and feature correlation learning. Specifically, we design a novel attention mechanism from three dimensions, namely spatial dimension, channel-wise dimension and hierarchical dimension. The adaptive spatial attention branch (ASAB) and the adaptive channel attention branch (ACAB) constitute the adaptive dual attention module (ADAM), which can capture the long-range spatial and channel-wise contextual information to expand the receptive field and distinguish different types of information for more effective feature representations. Furthermore, the adaptive hierarchical attention module (AHAM) can capture the long-range hierarchical contextual information to flexibly aggregate different feature maps by weights depending on the global context. The ADAM and AHAM cooperate to form an "attention in attention" structure, which means AHAM's inputs are enhanced by ASAB and ACAB. Experiments demonstrate the superiority of our method over state-of-the-art image restoration methods in both quantitative comparison and visual analysis.