An Accelerated Mixed Weighted-Unweighted MMSE Approach for MU-MIMO Beamforming

Precoding design based on weighted sum-rate (WSR) maximization is a fundamental problem in downlink multi-user multiple-input multiple-output (MU-MIMO) systems. While the weighted minimum mean-square error (WMMSE) algorithm is a standard solution, its high computational complexity--cubic in the number of base station antennas due to matrix inversions--hinders its application in latency-sensitive scenarios. To address this limitation, we propose a highly parallel algorithm based on a block coordinate descent framework. Our key innovation lies in updating the precoding matrix via block coordinate gradient descent, which avoids matrix inversions and relies solely on matrix multiplications, making it exceptionally amenable to GPU acceleration. We prove that the proposed algorithm converges to a stationary point of the WSR maximization problem. Furthermore, we introduce a two-stage warm-start strategy grounded in the sum mean-square error (MSE) minimization problem to accelerate convergence. We refer to our method as the Accelerated Mixed weighted-unweighted sum-MSE minimization (A-MMMSE) algorithm. Simulation results demonstrate that A-MMMSE matches the WSR performance of both conventional WMMSE and its enhanced variant, reduced-WMMSE, while achieving a substantial reduction in computational time across diverse system configurations.

When GNNs meet symmetry in ILPs: an orbit-based feature augmentation approach

A common characteristic in integer linear programs (ILPs) is symmetry, allowing variables to be permuted without altering the underlying problem structure. Recently, GNNs have emerged as a promising approach for solving ILPs. However, a significant challenge arises when applying GNNs to ILPs with symmetry: classic GNN architectures struggle to differentiate between symmetric variables, which limits their predictive accuracy. In this work, we investigate the properties of permutation equivariance and invariance in GNNs, particularly in relation to the inherent symmetry of ILP formulations. We reveal that the interaction between these two factors contributes to the difficulty of distinguishing between symmetric variables. To address this challenge, we explore the potential of feature augmentation and propose several guiding principles for constructing augmented features. Building on these principles, we develop an orbit-based augmentation scheme that first groups symmetric variables and then samples augmented features for each group from a discrete uniform distribution. Empirical results demonstrate that our proposed approach significantly enhances both training efficiency and predictive performance.

An Efficient Unsupervised Framework for Convex Quadratic Programs via Deep Unrolling

Quadratic programs (QPs) arise in various domains such as machine learning, finance, and control. Recently, learning-enhanced primal-dual hybrid gradient (PDHG) methods have shown great potential in addressing large-scale linear programs; however, this approach has not been extended to QPs. In this work, we focus on unrolling "PDQP", a PDHG algorithm specialized for convex QPs. Specifically, we propose a neural network model called "PDQP-net" to learn optimal QP solutions. Theoretically, we demonstrate that a PDQP-net of polynomial size can align with the PDQP algorithm, returning optimal primal-dual solution pairs. We propose an unsupervised method that incorporates KKT conditions into the loss function. Unlike the standard learning-to-optimize framework that requires optimization solutions generated by solvers, our unsupervised method adjusts the network weights directly from the evaluation of the primal-dual gap. This method has two benefits over supervised learning: first, it helps generate better primal-dual gap since the primal-dual gap is in the objective function; second, it does not require solvers. We show that PDQP-net trained in this unsupervised manner can effectively approximate optimal QP solutions. Extensive numerical experiments confirm our findings, indicating that using PDQP-net predictions to warm-start PDQP can achieve up to 45% acceleration on QP instances. Moreover, it achieves 14% to 31% acceleration on out-of-distribution instances.

PDHG-Unrolled Learning-to-Optimize Method for Large-Scale Linear Programming

Solving large-scale linear programming (LP) problems is an important task in various areas such as communication networks, power systems, finance and logistics. Recently, two distinct approaches have emerged to expedite LP solving: (i) First-order methods (FOMs); (ii) Learning to optimize (L2O). In this work, we propose an FOM-unrolled neural network (NN) called PDHG-Net, and propose a two-stage L2O method to solve large-scale LP problems. The new architecture PDHG-Net is designed by unrolling the recently emerged PDHG method into a neural network, combined with channel-expansion techniques borrowed from graph neural networks. We prove that the proposed PDHG-Net can recover PDHG algorithm, thus can approximate optimal solutions of LP instances with a polynomial number of neurons. We propose a two-stage inference approach: first use PDHG-Net to generate an approximate solution, and then apply PDHG algorithm to further improve the solution. Experiments show that our approach can significantly accelerate LP solving, achieving up to a 3$\times$ speedup compared to FOMs for large-scale LP problems.

The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights

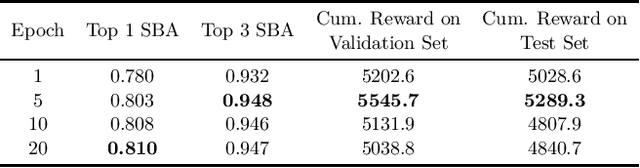
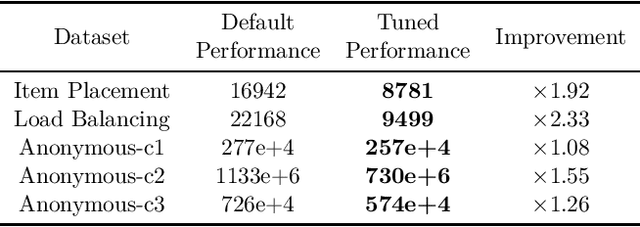
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.