First-order Policy Optimization for Robust Markov Decision Process

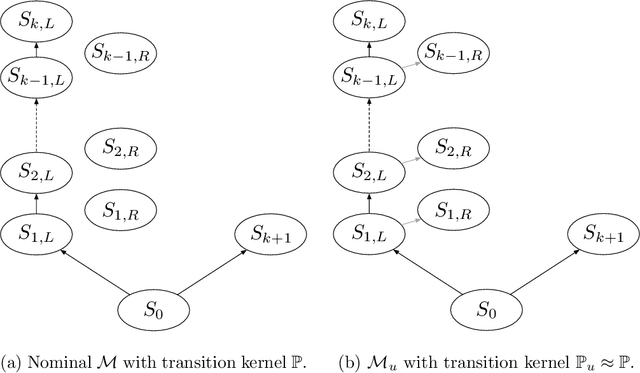
We consider the problem of solving robust Markov decision process (MDP), which involves a set of discounted, finite state, finite action space MDPs with uncertain transition kernels. The goal of planning is to find a robust policy that optimizes the worst-case values against the transition uncertainties, and thus encompasses the standard MDP planning as a special case. For $(\mathbf{s},\mathbf{a})$-rectangular uncertainty sets, we develop a policy-based first-order method, namely the robust policy mirror descent (RPMD), and establish an $\mathcal{O}(\log(1/\epsilon))$ and $\mathcal{O}(1/\epsilon)$ iteration complexity for finding an $\epsilon$-optimal policy, with two increasing-stepsize schemes. The prior convergence of RPMD is applicable to any Bregman divergence, provided the policy space has bounded radius measured by the divergence when centering at the initial policy. Moreover, when the Bregman divergence corresponds to the squared euclidean distance, we establish an $\mathcal{O}(\max \{1/\epsilon, 1/(\eta \epsilon^2)\})$ complexity of RPMD with any constant stepsize $\eta$. For a general class of Bregman divergences, a similar complexity is also established for RPMD with constant stepsizes, provided the uncertainty set satisfies the relative strong convexity. We further develop a stochastic variant, named SRPMD, when the first-order information is only available through online interactions with the nominal environment. For general Bregman divergences, we establish an $\mathcal{O}(1/\epsilon^2)$ and $\mathcal{O}(1/\epsilon^3)$ sample complexity with two increasing-stepsize schemes. For the euclidean Bregman divergence, we establish an $\mathcal{O}(1/\epsilon^3)$ sample complexity with constant stepsizes. To the best of our knowledge, all the aforementioned results appear to be new for policy-based first-order methods applied to the robust MDP problem.

Deep Forest with Hashing Screening and Window Screening

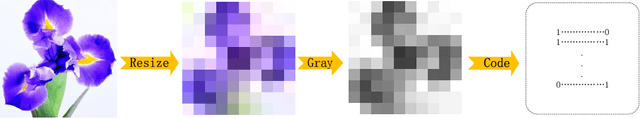
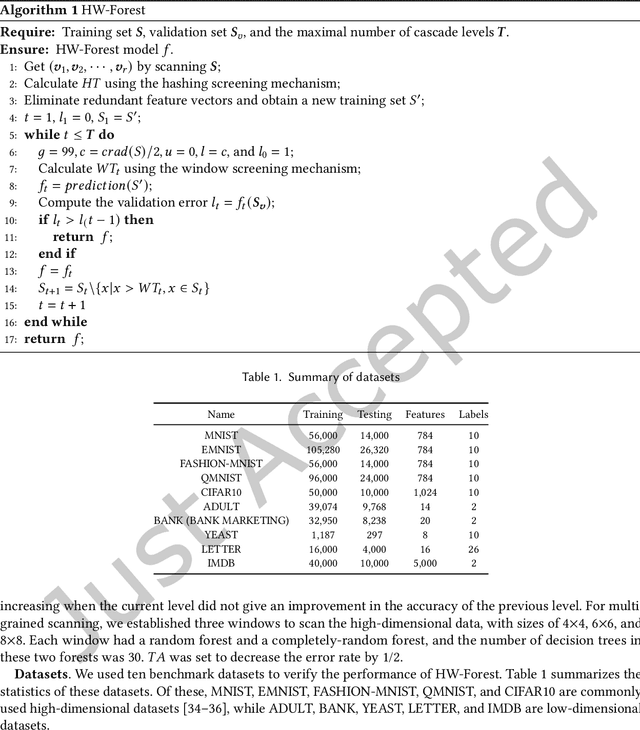
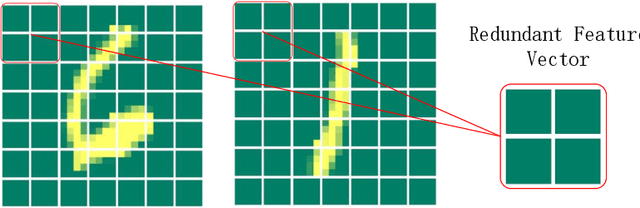
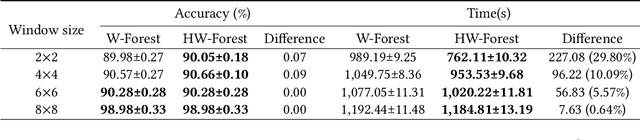
As a novel deep learning model, gcForest has been widely used in various applications. However, the current multi-grained scanning of gcForest produces many redundant feature vectors, and this increases the time cost of the model. To screen out redundant feature vectors, we introduce a hashing screening mechanism for multi-grained scanning and propose a model called HW-Forest which adopts two strategies, hashing screening and window screening. HW-Forest employs perceptual hashing algorithm to calculate the similarity between feature vectors in hashing screening strategy, which is used to remove the redundant feature vectors produced by multi-grained scanning and can significantly decrease the time cost and memory consumption. Furthermore, we adopt a self-adaptive instance screening strategy to improve the performance of our approach, called window screening, which can achieve higher accuracy without hyperparameter tuning on different datasets. Our experimental results show that HW-Forest has higher accuracy than other models, and the time cost is also reduced.

Robust Time Series Dissimilarity Measure for Outlier Detection and Periodicity Detection

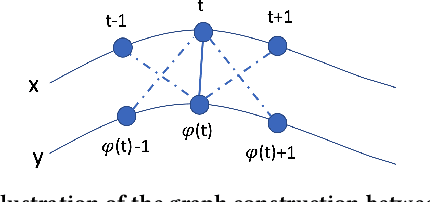
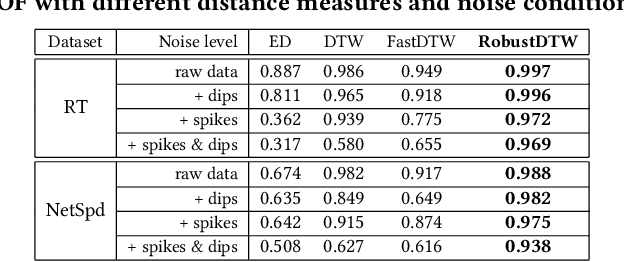
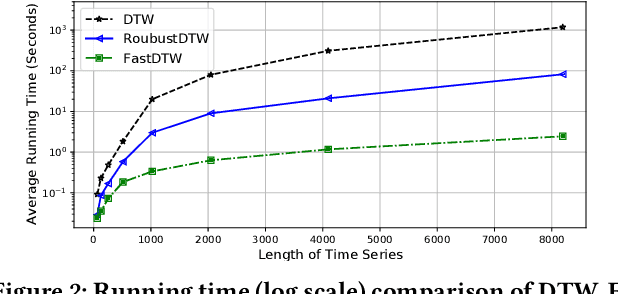
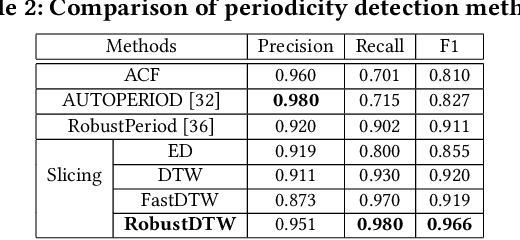
Dynamic time warping (DTW) is an effective dissimilarity measure in many time series applications. Despite its popularity, it is prone to noises and outliers, which leads to singularity problem and bias in the measurement. The time complexity of DTW is quadratic to the length of time series, making it inapplicable in real-time applications. In this paper, we propose a novel time series dissimilarity measure named RobustDTW to reduce the effects of noises and outliers. Specifically, the RobustDTW estimates the trend and optimizes the time warp in an alternating manner by utilizing our designed temporal graph trend filtering. To improve efficiency, we propose a multi-level framework that estimates the trend and the warp function at a lower resolution, and then repeatedly refines them at a higher resolution. Based on the proposed RobustDTW, we further extend it to periodicity detection and outlier time series detection. Experiments on real-world datasets demonstrate the superior performance of RobustDTW compared to DTW variants in both outlier time series detection and periodicity detection.

Benchmarking Domain Generalization on EEG-based Emotion Recognition

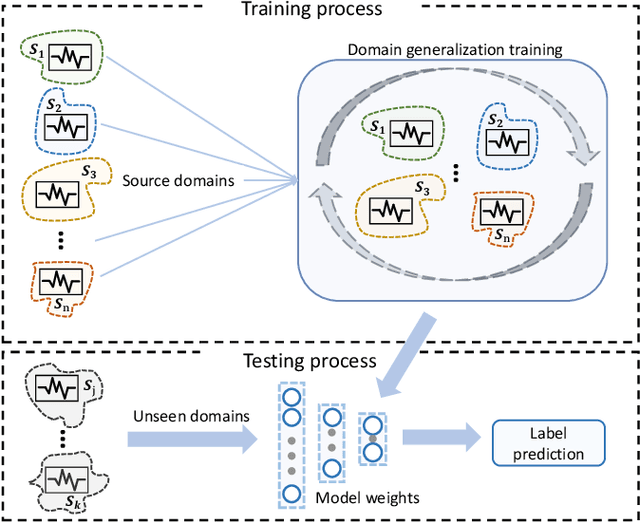
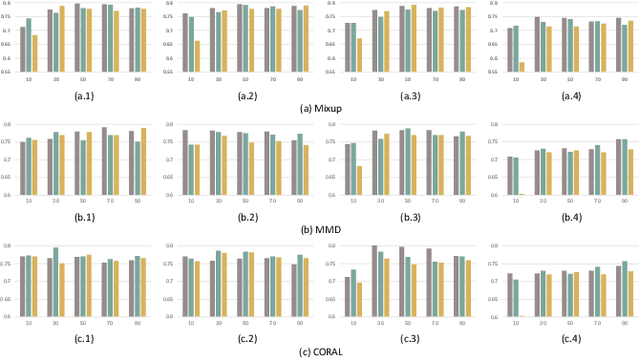
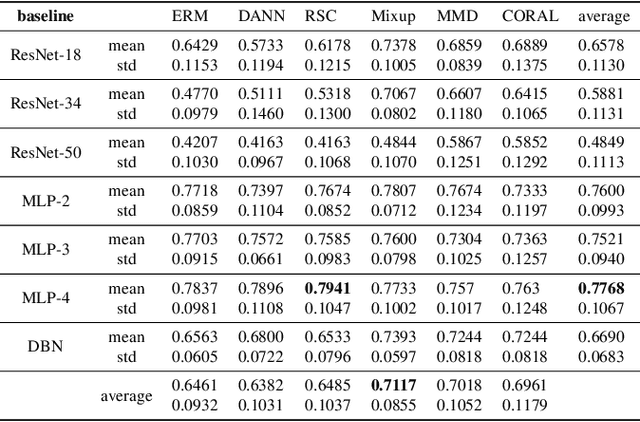
Electroencephalography (EEG) based emotion recognition has demonstrated tremendous improvement in recent years. Specifically, numerous domain adaptation (DA) algorithms have been exploited in the past five years to enhance the generalization of emotion recognition models across subjects. The DA methods assume that calibration data (although unlabeled) exists in the target domain (new user). However, this assumption conflicts with the application scenario that the model should be deployed without the time-consuming calibration experiments. We argue that domain generalization (DG) is more reasonable than DA in these applications. DG learns how to generalize to unseen target domains by leveraging knowledge from multiple source domains, which provides a new possibility to train general models. In this paper, we for the first time benchmark state-of-the-art DG algorithms on EEG-based emotion recognition. Since convolutional neural network (CNN), deep brief network (DBN) and multilayer perceptron (MLP) have been proved to be effective emotion recognition models, we use these three models as solid baselines. Experimental results show that DG achieves an accuracy of up to 79.41\% on the SEED dataset for recognizing three emotions, indicting the potential of DG in zero-training emotion recognition when multiple sources are available.

Robust Single Image Dehazing Based on Consistent and Contrast-Assisted Reconstruction

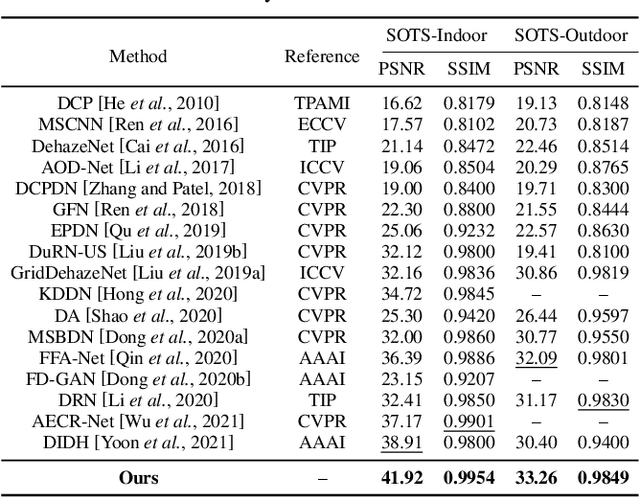
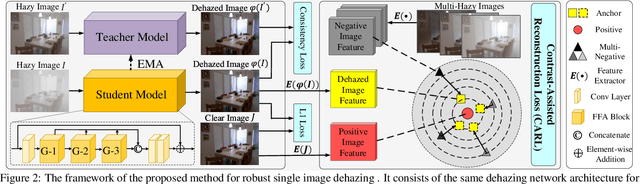
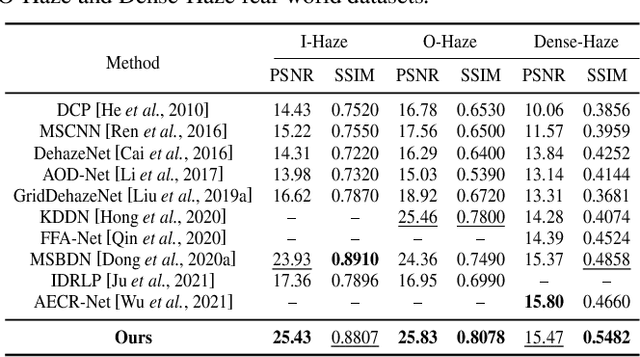
Single image dehazing as a fundamental low-level vision task, is essential for the development of robust intelligent surveillance system. In this paper, we make an early effort to consider dehazing robustness under variational haze density, which is a realistic while under-studied problem in the research filed of singe image dehazing. To properly address this problem, we propose a novel density-variational learning framework to improve the robustness of the image dehzing model assisted by a variety of negative hazy images, to better deal with various complex hazy scenarios. Specifically, the dehazing network is optimized under the consistency-regularized framework with the proposed Contrast-Assisted Reconstruction Loss (CARL). The CARL can fully exploit the negative information to facilitate the traditional positive-orient dehazing objective function, by squeezing the dehazed image to its clean target from different directions. Meanwhile, the consistency regularization keeps consistent outputs given multi-level hazy images, thus improving the model robustness. Extensive experimental results on two synthetic and three real-world datasets demonstrate that our method significantly surpasses the state-of-the-art approaches.

DSRRTracker: Dynamic Search Region Refinement for Attention-based Siamese Multi-Object Tracking

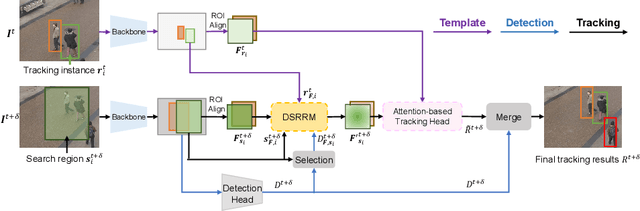
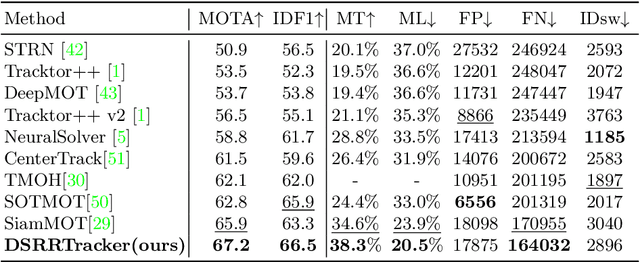
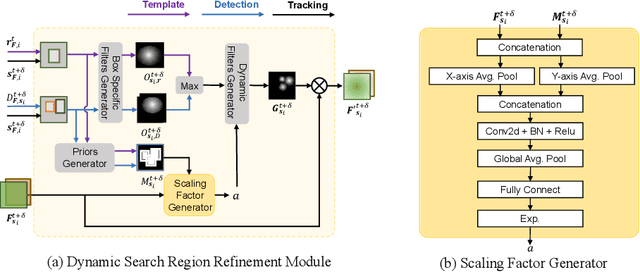
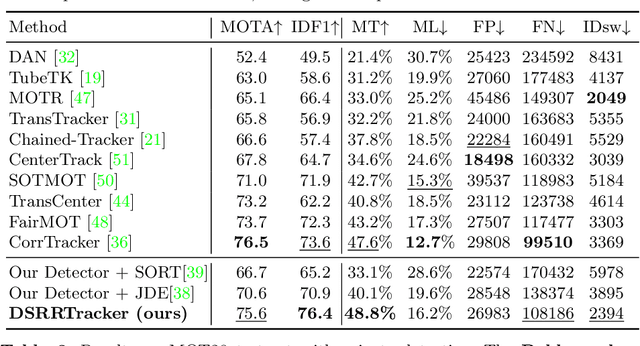
Many multi-object tracking (MOT) methods follow the framework of "tracking by detection", which associates the target objects-of-interest based on the detection results. However, due to the separate models for detection and association, the tracking results are not optimal.Moreover, the speed is limited by some cumbersome association methods to achieve high tracking performance. In this work, we propose an end-to-end MOT method, with a Gaussian filter-inspired dynamic search region refinement module to dynamically filter and refine the search region by considering both the template information from the past frames and the detection results from the current frame with little computational burden, and a lightweight attention-based tracking head to achieve the effective fine-grained instance association. Extensive experiments and ablation study on MOT17 and MOT20 datasets demonstrate that our method can achieve the state-of-the-art performance with reasonable speed.

OPP-Miner: Order-preserving sequential pattern mining

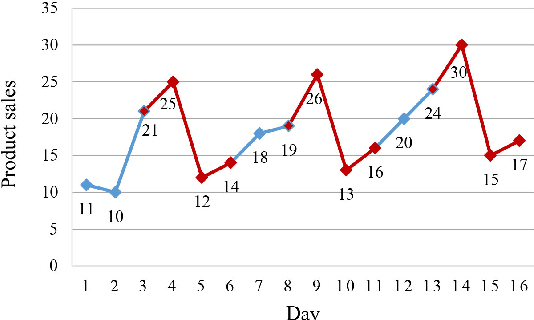
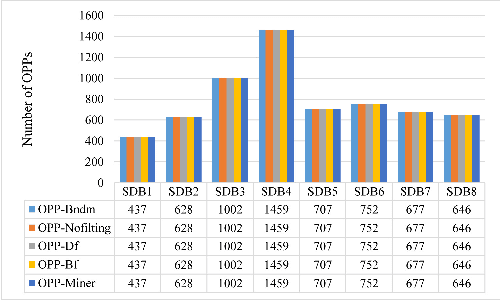
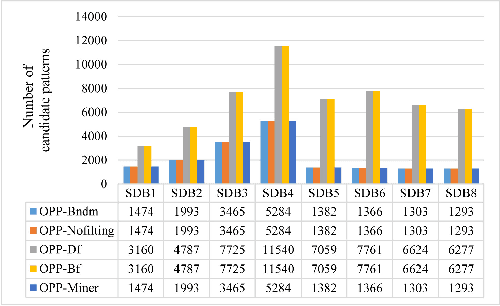
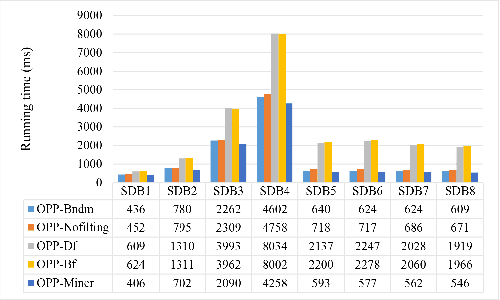
A time series is a collection of measurements in chronological order. Discovering patterns from time series is useful in many domains, such as stock analysis, disease detection, and weather forecast. To discover patterns, existing methods often convert time series data into another form, such as nominal/symbolic format, to reduce dimensionality, which inevitably deviates the data values. Moreover, existing methods mainly neglect the order relationships between time series values. To tackle these issues, inspired by order-preserving matching, this paper proposes an Order-Preserving sequential Pattern (OPP) mining method, which represents patterns based on the order relationships of the time series data. An inherent advantage of such representation is that the trend of a time series can be represented by the relative order of the values underneath the time series data. To obtain frequent trends in time series, we propose the OPP-Miner algorithm to mine patterns with the same trend (sub-sequences with the same relative order). OPP-Miner employs the filtration and verification strategies to calculate the support and uses pattern fusion strategy to generate candidate patterns. To compress the result set, we also study finding the maximal OPPs. Experiments validate that OPP-Miner is not only efficient and scalable but can also discover similar sub-sequences in time series. In addition, case studies show that our algorithms have high utility in analyzing the COVID-19 epidemic by identifying critical trends and improve the clustering performance.

Noise Regularizes Over-parameterized Rank One Matrix Recovery, Provably

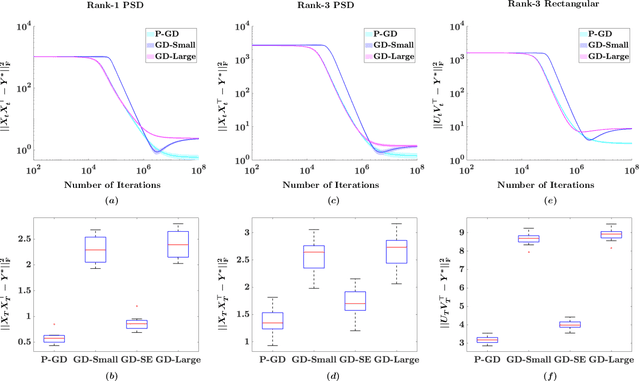
We investigate the role of noise in optimization algorithms for learning over-parameterized models. Specifically, we consider the recovery of a rank one matrix $Y^*\in R^{d\times d}$ from a noisy observation $Y$ using an over-parameterization model. We parameterize the rank one matrix $Y^*$ by $XX^\top$, where $X\in R^{d\times d}$. We then show that under mild conditions, the estimator, obtained by the randomly perturbed gradient descent algorithm using the square loss function, attains a mean square error of $O(\sigma^2/d)$, where $\sigma^2$ is the variance of the observational noise. In contrast, the estimator obtained by gradient descent without random perturbation only attains a mean square error of $O(\sigma^2)$. Our result partially justifies the implicit regularization effect of noise when learning over-parameterized models, and provides new understanding of training over-parameterized neural networks.

Homotopic Policy Mirror Descent: Policy Convergence, Implicit Regularization, and Improved Sample Complexity

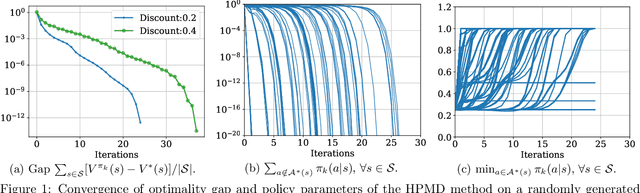
We propose the homotopic policy mirror descent (HPMD) method for solving discounted, infinite horizon MDPs with finite state and action space, and study its policy convergence. We report three properties that seem to be new in the literature of policy gradient methods: (1) HPMD exhibits global linear convergence of the value optimality gap, and local superlinear convergence of the policy to the set of optimal policies with order $\gamma^{-2}$. The superlinear convergence of the policy takes effect after no more than $\mathcal{O}(\log(1/\Delta^*))$ number of iterations, where $\Delta^*$ is defined via a gap quantity associated with the optimal state-action value function; (2) HPMD also exhibits last-iterate convergence of the policy, with the limiting policy corresponding exactly to the optimal policy with the maximal entropy for every state. No regularization is added to the optimization objective and hence the second observation arises solely as an algorithmic property of the homotopic policy gradient method. (3) For the stochastic HPMD method, we further demonstrate a better than $\mathcal{O}(|\mathcal{S}| |\mathcal{A}| / \epsilon^2)$ sample complexity for small optimality gap $\epsilon$, when assuming a generative model for policy evaluation.

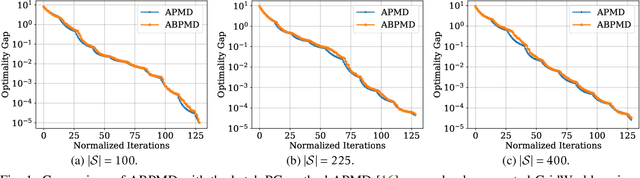
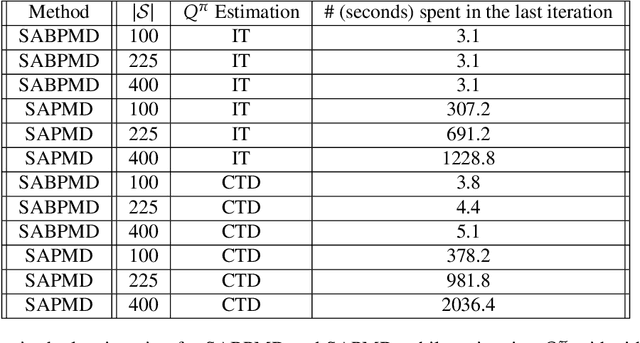
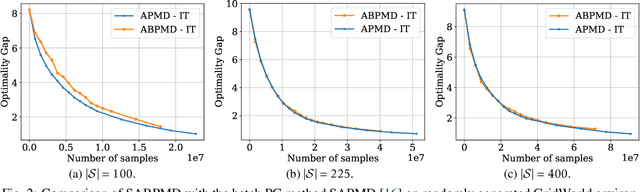
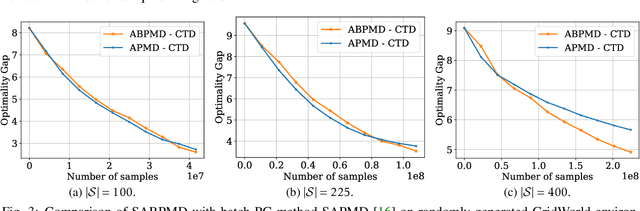
Block Policy Mirror Descent

In this paper, we present a new class of policy gradient (PG) methods, namely the block policy mirror descent (BPMD) methods for solving a class of regularized reinforcement learning (RL) problems with (strongly) convex regularizers. Compared to the traditional PG methods with batch update rule, which visit and update the policy for every state, BPMD methods have cheap per-iteration computation via a partial update rule that performs the policy update on a sampled state. Despite the nonconvex nature of the problem and a partial update rule, BPMD methods achieve fast linear convergence to the global optimality. We further extend BPMD methods to the stochastic setting, by utilizing stochastic first-order information constructed from samples. We establish $\cO(1/\epsilon)$ (resp. $\cO(1/\epsilon^2)$) sample complexity for the strongly convex (resp. non-strongly convex) regularizers, with different procedures for constructing the stochastic first-order information, where $\epsilon$ denotes the target accuracy. To the best of our knowledge, this is the first time that block coordinate descent methods have been developed and analyzed for policy optimization in reinforcement learning.