Policy Gradient Optimzation for Bayesian-Risk MDPs with General Convex Losses

Motivated by many application problems, we consider Markov decision processes (MDPs) with a general loss function and unknown parameters. To mitigate the epistemic uncertainty associated with unknown parameters, we take a Bayesian approach to estimate the parameters from data and impose a coherent risk functional (with respect to the Bayesian posterior distribution) on the loss. Since this formulation usually does not satisfy the interchangeability principle, it does not admit Bellman equations and cannot be solved by approaches based on dynamic programming. Therefore, We propose a policy gradient optimization method, leveraging the dual representation of coherent risk measures and extending the envelope theorem to continuous cases. We then show the stationary analysis of the algorithm with a convergence rate of $O(T^{-1/2}+r^{-1/2})$, where $T$ is the number of policy gradient iterations and $r$ is the sample size of the gradient estimator. We further extend our algorithm to an episodic setting, and establish the global convergence of the extended algorithm and provide bounds on the number of iterations needed to achieve an error bound $O(\epsilon)$ in each episode.

Online Bayesian Risk-Averse Reinforcement Learning

In this paper, we study the Bayesian risk-averse formulation in reinforcement learning (RL). To address the epistemic uncertainty due to a lack of data, we adopt the Bayesian Risk Markov Decision Process (BRMDP) to account for the parameter uncertainty of the unknown underlying model. We derive the asymptotic normality that characterizes the difference between the Bayesian risk value function and the original value function under the true unknown distribution. The results indicate that the Bayesian risk-averse approach tends to pessimistically underestimate the original value function. This discrepancy increases with stronger risk aversion and decreases as more data become available. We then utilize this adaptive property in the setting of online RL as well as online contextual multi-arm bandits (CMAB), a special case of online RL. We provide two procedures using posterior sampling for both the general RL problem and the CMAB problem. We establish a sub-linear regret bound, with the regret defined as the conventional regret for both the RL and CMAB settings. Additionally, we establish a sub-linear regret bound for the CMAB setting with the regret defined as the Bayesian risk regret. Finally, we conduct numerical experiments to demonstrate the effectiveness of the proposed algorithm in addressing epistemic uncertainty and verifying the theoretical properties.

Ranking and Selection with Simultaneous Input Data Collection

In this paper, we propose a general and novel formulation of ranking and selection with the existence of streaming input data. The collection of multiple streams of such data may consume different types of resources, and hence can be conducted simultaneously. To utilize the streaming input data, we aggregate simulation outputs generated under heterogeneous input distributions over time to form a performance estimator. By characterizing the asymptotic behavior of the performance estimators, we formulate two optimization problems to optimally allocate budgets for collecting input data and running simulations. We then develop a multi-stage simultaneous budget allocation procedure and provide its statistical guarantees such as consistency and asymptotic normality. We conduct several numerical studies to demonstrate the competitive performance of the proposed procedure.

Reusing Historical Trajectories in Natural Policy Gradient via Importance Sampling: Convergence and Convergence Rate

Reinforcement learning provides a mathematical framework for learning-based control, whose success largely depends on the amount of data it can utilize. The efficient utilization of historical trajectories obtained from previous policies is essential for expediting policy optimization. Empirical evidence has shown that policy gradient methods based on importance sampling work well. However, existing literature often neglect the interdependence between trajectories from different iterations, and the good empirical performance lacks a rigorous theoretical justification. In this paper, we study a variant of the natural policy gradient method with reusing historical trajectories via importance sampling. We show that the bias of the proposed estimator of the gradient is asymptotically negligible, the resultant algorithm is convergent, and reusing past trajectories helps improve the convergence rate. We further apply the proposed estimator to popular policy optimization algorithms such as trust region policy optimization. Our theoretical results are verified on classical benchmarks.

Bayesian Risk-Averse Q-Learning with Streaming Observations

We consider a robust reinforcement learning problem, where a learning agent learns from a simulated training environment. To account for the model mis-specification between this training environment and the real environment due to lack of data, we adopt a formulation of Bayesian risk MDP (BRMDP) with infinite horizon, which uses Bayesian posterior to estimate the transition model and impose a risk functional to account for the model uncertainty. Observations from the real environment that is out of the agent's control arrive periodically and are utilized by the agent to update the Bayesian posterior to reduce model uncertainty. We theoretically demonstrate that BRMDP balances the trade-off between robustness and conservativeness, and we further develop a multi-stage Bayesian risk-averse Q-learning algorithm to solve BRMDP with streaming observations from real environment. The proposed algorithm learns a risk-averse yet optimal policy that depends on the availability of real-world observations. We provide a theoretical guarantee of strong convergence for the proposed algorithm.

Risk-averse Contextual Multi-armed Bandit Problem with Linear Payoffs

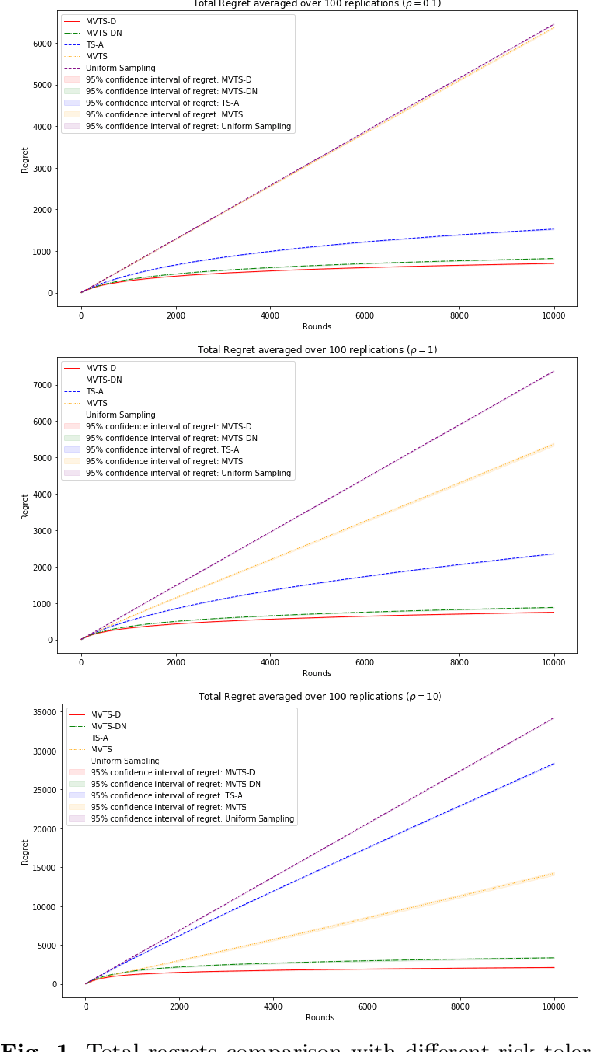
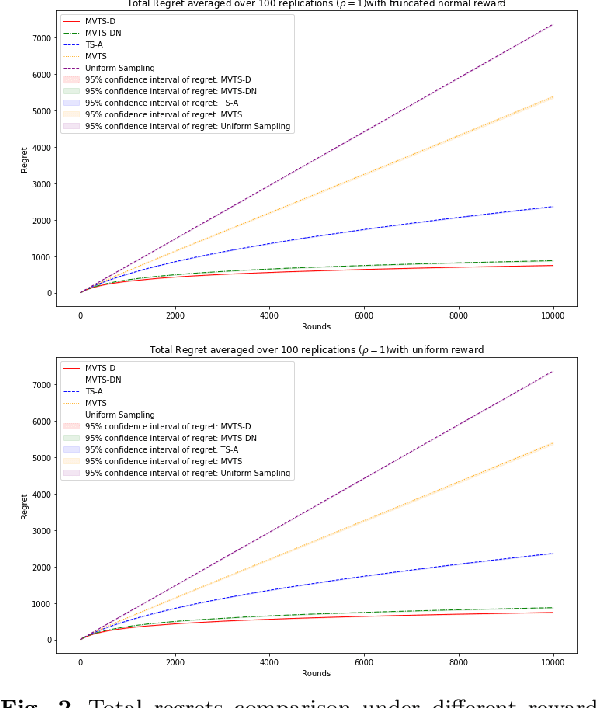
In this paper we consider the contextual multi-armed bandit problem for linear payoffs under a risk-averse criterion. At each round, contexts are revealed for each arm, and the decision maker chooses one arm to pull and receives the corresponding reward. In particular, we consider mean-variance as the risk criterion, and the best arm is the one with the largest mean-variance reward. We apply the Thompson Sampling algorithm for the disjoint model, and provide a comprehensive regret analysis for a variant of the proposed algorithm. For $T$ rounds, $K$ actions, and $d$-dimensional feature vectors, we prove a regret bound of $O((1+\rho+\frac{1}{\rho}) d\ln T \ln \frac{K}{\delta}\sqrt{d K T^{1+2\epsilon} \ln \frac{K}{\delta} \frac{1}{\epsilon}})$ that holds with probability $1-\delta$ under the mean-variance criterion with risk tolerance $\rho$, for any $0<\epsilon<\frac{1}{2}$, $0<\delta<1$. The empirical performance of our proposed algorithms is demonstrated via a portfolio selection problem.

Robust Multi-Objective Bayesian Optimization Under Input Noise

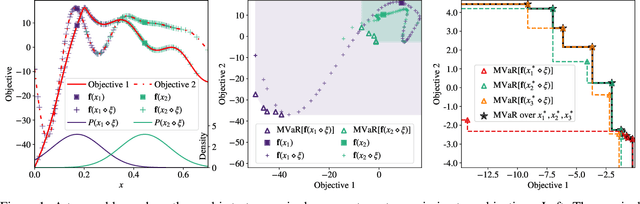
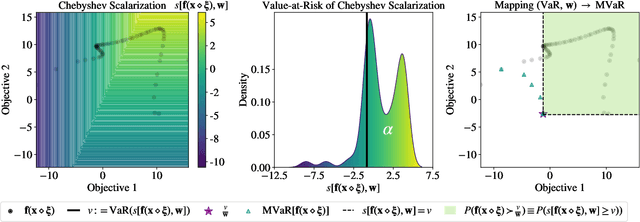
Bayesian optimization (BO) is a sample-efficient approach for tuning design parameters to optimize expensive-to-evaluate, black-box performance metrics. In many manufacturing processes, the design parameters are subject to random input noise, resulting in a product that is often less performant than expected. Although BO methods have been proposed for optimizing a single objective under input noise, no existing method addresses the practical scenario where there are multiple objectives that are sensitive to input perturbations. In this work, we propose the first multi-objective BO method that is robust to input noise. We formalize our goal as optimizing the multivariate value-at-risk (MVaR), a risk measure of the uncertain objectives. Since directly optimizing MVaR is computationally infeasible in many settings, we propose a scalable, theoretically-grounded approach for optimizing MVaR using random scalarizations. Empirically, we find that our approach significantly outperforms alternative methods and efficiently identifies optimal robust designs that will satisfy specifications across multiple metrics with high probability.

Noise Regularizes Over-parameterized Rank One Matrix Recovery, Provably

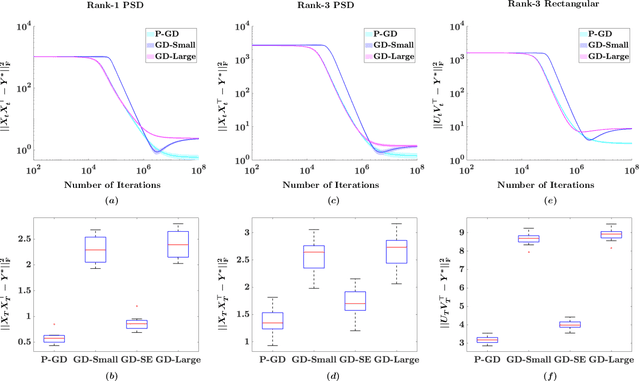
We investigate the role of noise in optimization algorithms for learning over-parameterized models. Specifically, we consider the recovery of a rank one matrix $Y^*\in R^{d\times d}$ from a noisy observation $Y$ using an over-parameterization model. We parameterize the rank one matrix $Y^*$ by $XX^\top$, where $X\in R^{d\times d}$. We then show that under mild conditions, the estimator, obtained by the randomly perturbed gradient descent algorithm using the square loss function, attains a mean square error of $O(\sigma^2/d)$, where $\sigma^2$ is the variance of the observational noise. In contrast, the estimator obtained by gradient descent without random perturbation only attains a mean square error of $O(\sigma^2)$. Our result partially justifies the implicit regularization effect of noise when learning over-parameterized models, and provides new understanding of training over-parameterized neural networks.

Noisy Gradient Descent Converges to Flat Minima for Nonconvex Matrix Factorization

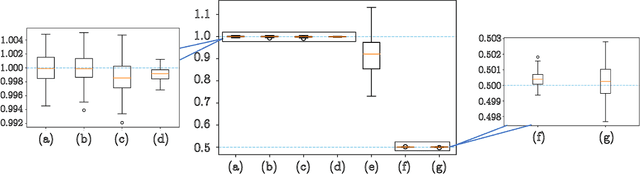
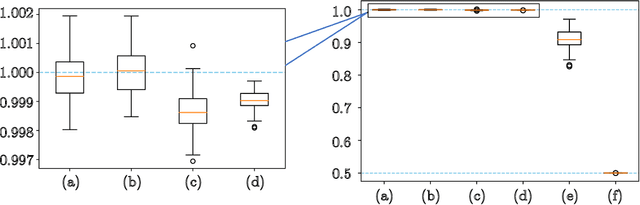
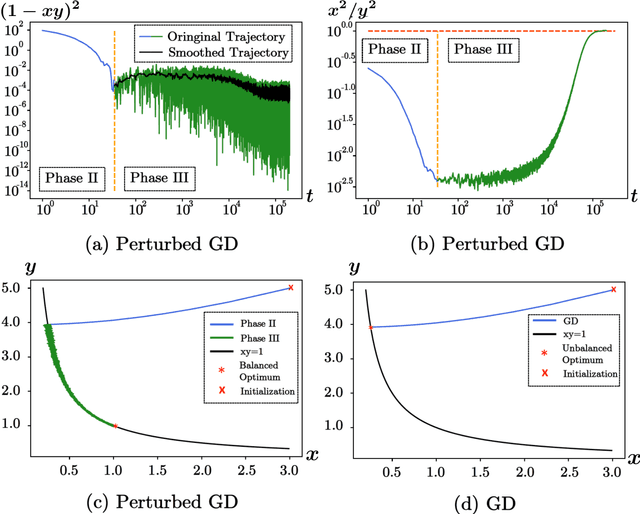
Numerous empirical evidences have corroborated the importance of noise in nonconvex optimization problems. The theory behind such empirical observations, however, is still largely unknown. This paper studies this fundamental problem through investigating the nonconvex rectangular matrix factorization problem, which has infinitely many global minima due to rotation and scaling invariance. Hence, gradient descent (GD) can converge to any optimum, depending on the initialization. In contrast, we show that a perturbed form of GD with an arbitrary initialization converges to a global optimum that is uniquely determined by the injected noise. Our result implies that the noise imposes implicit bias towards certain optima. Numerical experiments are provided to support our theory.

Bayesian Optimization of Risk Measures

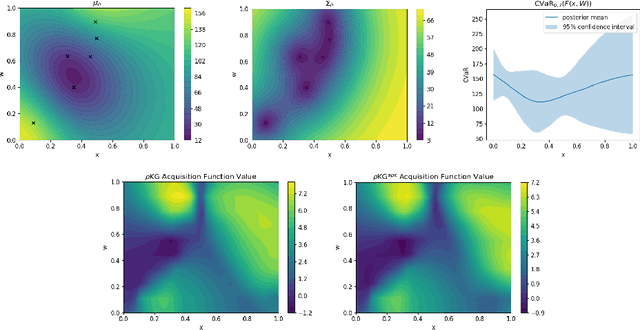
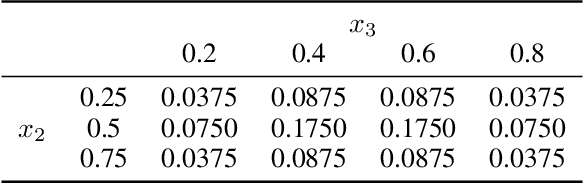
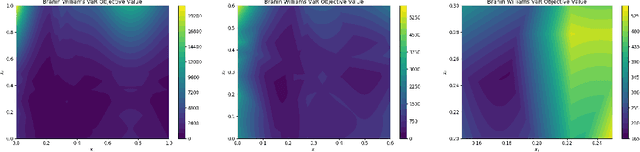
We consider Bayesian optimization of objective functions of the form $\rho[ F(x, W) ]$, where $F$ is a black-box expensive-to-evaluate function and $\rho$ denotes either the VaR or CVaR risk measure, computed with respect to the randomness induced by the environmental random variable $W$. Such problems arise in decision making under uncertainty, such as in portfolio optimization and robust systems design. We propose a family of novel Bayesian optimization algorithms that exploit the structure of the objective function to substantially improve sampling efficiency. Instead of modeling the objective function directly as is typical in Bayesian optimization, these algorithms model $F$ as a Gaussian process, and use the implied posterior on the objective function to decide which points to evaluate. We demonstrate the effectiveness of our approach in a variety of numerical experiments.