CHAINSFORMER: Numerical Reasoning on Knowledge Graphs from a Chain Perspective

Reasoning over Knowledge Graphs (KGs) plays a pivotal role in knowledge graph completion or question answering systems, providing richer and more accurate triples and attributes. As numerical attributes become increasingly essential in characterizing entities and relations in KGs, the ability to reason over these attributes has gained significant importance. Existing graph-based methods such as Graph Neural Networks (GNNs) and Knowledge Graph Embeddings (KGEs), primarily focus on aggregating homogeneous local neighbors and implicitly embedding diverse triples. However, these approaches often fail to fully leverage the potential of logical paths within the graph, limiting their effectiveness in exploiting the reasoning process. To address these limitations, we propose ChainsFormer, a novel chain-based framework designed to support numerical reasoning. Chainsformer not only explicitly constructs logical chains but also expands the reasoning depth to multiple hops. Specially, we introduces Relation-Attribute Chains (RA-Chains), a specialized logic chain, to model sequential reasoning patterns. ChainsFormer captures the step-by-step nature of multi-hop reasoning along RA-Chains by employing sequential in-context learning. To mitigate the impact of noisy chains, we propose a hyperbolic affinity scoring mechanism that selects relevant logic chains in a variable-resolution space. Furthermore, ChainsFormer incorporates an attention-based numerical reasoner to identify critical reasoning paths, enhancing both reasoning accuracy and transparency. Experimental results demonstrate that ChainsFormer significantly outperforms state-of-the-art methods, achieving up to a 20.0% improvement in performance. The implementations are available at https://github.com/zhaodazhuang2333/ChainsFormer.

AceParse: A Comprehensive Dataset with Diverse Structured Texts for Academic Literature Parsing

With the development of data-centric AI, the focus has shifted from model-driven approaches to improving data quality. Academic literature, as one of the crucial types, is predominantly stored in PDF formats and needs to be parsed into texts before further processing. However, parsing diverse structured texts in academic literature remains challenging due to the lack of datasets that cover various text structures. In this paper, we introduce AceParse, the first comprehensive dataset designed to support the parsing of a wide range of structured texts, including formulas, tables, lists, algorithms, and sentences with embedded mathematical expressions. Based on AceParse, we fine-tuned a multimodal model, named AceParser, which accurately parses various structured texts within academic literature. This model outperforms the previous state-of-the-art by 4.1% in terms of F1 score and by 5% in Jaccard Similarity, demonstrating the potential of multimodal models in academic literature parsing. Our dataset is available at https://github.com/JHW5981/AceParse.

AutoFAIR : Automatic Data FAIRification via Machine Reading

The explosive growth of data fuels data-driven research, facilitating progress across diverse domains. The FAIR principles emerge as a guiding standard, aiming to enhance the findability, accessibility, interoperability, and reusability of data. However, current efforts primarily focus on manual data FAIRification, which can only handle targeted data and lack efficiency. To address this issue, we propose AutoFAIR, an architecture designed to enhance data FAIRness automately. Firstly, We align each data and metadata operation with specific FAIR indicators to guide machine-executable actions. Then, We utilize Web Reader to automatically extract metadata based on language models, even in the absence of structured data webpage schemas. Subsequently, FAIR Alignment is employed to make metadata comply with FAIR principles by ontology guidance and semantic matching. Finally, by applying AutoFAIR to various data, especially in the field of mountain hazards, we observe significant improvements in findability, accessibility, interoperability, and reusability of data. The FAIRness scores before and after applying AutoFAIR indicate enhanced data value.

OXYGENERATOR: Reconstructing Global Ocean Deoxygenation Over a Century with Deep Learning

Accurately reconstructing the global ocean deoxygenation over a century is crucial for assessing and protecting marine ecosystem. Existing expert-dominated numerical simulations fail to catch up with the dynamic variation caused by global warming and human activities. Besides, due to the high-cost data collection, the historical observations are severely sparse, leading to big challenge for precise reconstruction. In this work, we propose OxyGenerator, the first deep learning based model, to reconstruct the global ocean deoxygenation from 1920 to 2023. Specifically, to address the heterogeneity across large temporal and spatial scales, we propose zoning-varying graph message-passing to capture the complex oceanographic correlations between missing values and sparse observations. Additionally, to further calibrate the uncertainty, we incorporate inductive bias from dissolved oxygen (DO) variations and chemical effects. Compared with in-situ DO observations, OxyGenerator significantly outperforms CMIP6 numerical simulations, reducing MAPE by 38.77%, demonstrating a promising potential to understand the "breathless ocean" in data-driven manner.

Temporal Generalization Estimation in Evolving Graphs

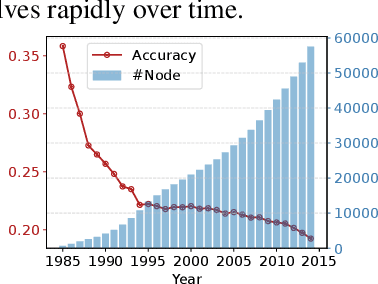
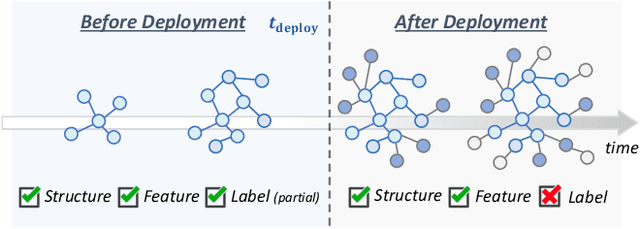
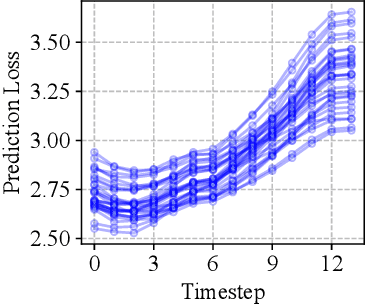
Graph Neural Networks (GNNs) are widely deployed in vast fields, but they often struggle to maintain accurate representations as graphs evolve. We theoretically establish a lower bound, proving that under mild conditions, representation distortion inevitably occurs over time. To estimate the temporal distortion without human annotation after deployment, one naive approach is to pre-train a recurrent model (e.g., RNN) before deployment and use this model afterwards, but the estimation is far from satisfactory. In this paper, we analyze the representation distortion from an information theory perspective, and attribute it primarily to inaccurate feature extraction during evolution. Consequently, we introduce Smart, a straightforward and effective baseline enhanced by an adaptive feature extractor through self-supervised graph reconstruction. In synthetic random graphs, we further refine the former lower bound to show the inevitable distortion over time and empirically observe that Smart achieves good estimation performance. Moreover, we observe that Smart consistently shows outstanding generalization estimation on four real-world evolving graphs. The ablation studies underscore the necessity of graph reconstruction. For example, on OGB-arXiv dataset, the estimation metric MAPE deteriorates from 2.19% to 8.00% without reconstruction.

AceMap: Knowledge Discovery through Academic Graph

The exponential growth of scientific literature requires effective management and extraction of valuable insights. While existing scientific search engines excel at delivering search results based on relational databases, they often neglect the analysis of collaborations between scientific entities and the evolution of ideas, as well as the in-depth analysis of content within scientific publications. The representation of heterogeneous graphs and the effective measurement, analysis, and mining of such graphs pose significant challenges. To address these challenges, we present AceMap, an academic system designed for knowledge discovery through academic graph. We present advanced database construction techniques to build the comprehensive AceMap database with large-scale academic publications that contain rich visual, textual, and numerical information. AceMap also employs innovative visualization, quantification, and analysis methods to explore associations and logical relationships among academic entities. AceMap introduces large-scale academic network visualization techniques centered on nebular graphs, providing a comprehensive view of academic networks from multiple perspectives. In addition, AceMap proposes a unified metric based on structural entropy to quantitatively measure the knowledge content of different academic entities. Moreover, AceMap provides advanced analysis capabilities, including tracing the evolution of academic ideas through citation relationships and concept co-occurrence, and generating concise summaries informed by this evolutionary process. In addition, AceMap uses machine reading methods to generate potential new ideas at the intersection of different fields. Exploring the integration of large language models and knowledge graphs is a promising direction for future research in idea evolution. Please visit \url{https://www.acemap.info} for further exploration.

Graph Out-of-Distribution Generalization with Controllable Data Augmentation

Graph Neural Network (GNN) has demonstrated extraordinary performance in classifying graph properties. However, due to the selection bias of training and testing data (e.g., training on small graphs and testing on large graphs, or training on dense graphs and testing on sparse graphs), distribution deviation is widespread. More importantly, we often observe \emph{hybrid structure distribution shift} of both scale and density, despite of one-sided biased data partition. The spurious correlations over hybrid distribution deviation degrade the performance of previous GNN methods and show large instability among different datasets. To alleviate this problem, we propose \texttt{OOD-GMixup} to jointly manipulate the training distribution with \emph{controllable data augmentation} in metric space. Specifically, we first extract the graph rationales to eliminate the spurious correlations due to irrelevant information. Secondly, we generate virtual samples with perturbation on graph rationale representation domain to obtain potential OOD training samples. Finally, we propose OOD calibration to measure the distribution deviation of virtual samples by leveraging Extreme Value Theory, and further actively control the training distribution by emphasizing the impact of virtual OOD samples. Extensive studies on several real-world datasets on graph classification demonstrate the superiority of our proposed method over state-of-the-art baselines.

Spatio-Temporal Graph Few-Shot Learning with Cross-City Knowledge Transfer

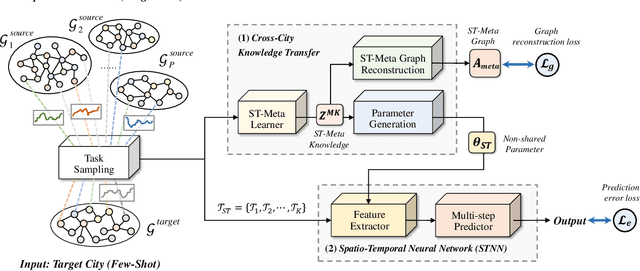
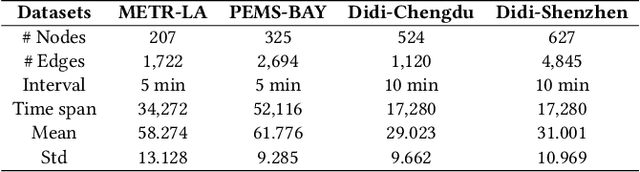
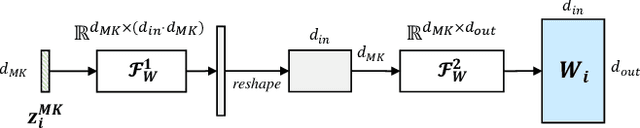
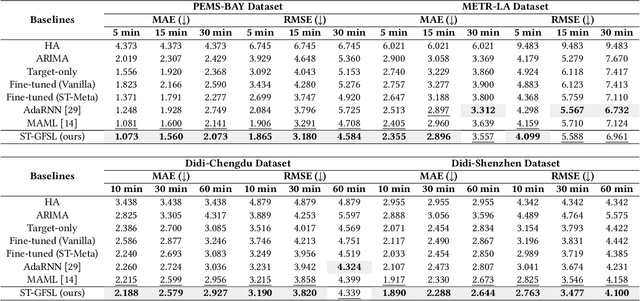
Spatio-temporal graph learning is a key method for urban computing tasks, such as traffic flow, taxi demand and air quality forecasting. Due to the high cost of data collection, some developing cities have few available data, which makes it infeasible to train a well-performed model. To address this challenge, cross-city knowledge transfer has shown its promise, where the model learned from data-sufficient cities is leveraged to benefit the learning process of data-scarce cities. However, the spatio-temporal graphs among different cities show irregular structures and varied features, which limits the feasibility of existing Few-Shot Learning (\emph{FSL}) methods. Therefore, we propose a model-agnostic few-shot learning framework for spatio-temporal graph called ST-GFSL. Specifically, to enhance feature extraction by transfering cross-city knowledge, ST-GFSL proposes to generate non-shared parameters based on node-level meta knowledge. The nodes in target city transfer the knowledge via parameter matching, retrieving from similar spatio-temporal characteristics. Furthermore, we propose to reconstruct the graph structure during meta-learning. The graph reconstruction loss is defined to guide structure-aware learning, avoiding structure deviation among different datasets. We conduct comprehensive experiments on four traffic speed prediction benchmarks and the results demonstrate the effectiveness of ST-GFSL compared with state-of-the-art methods.

Geometer: Graph Few-Shot Class-Incremental Learning via Prototype Representation

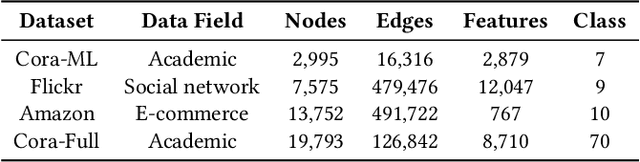
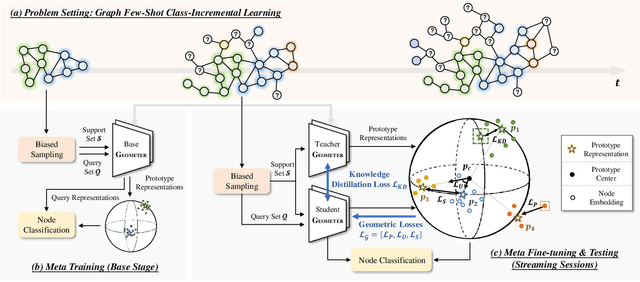
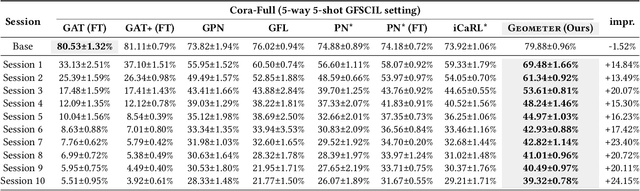
With the tremendous expansion of graphs data, node classification shows its great importance in many real-world applications. Existing graph neural network based methods mainly focus on classifying unlabeled nodes within fixed classes with abundant labeling. However, in many practical scenarios, graph evolves with emergence of new nodes and edges. Novel classes appear incrementally along with few labeling due to its newly emergence or lack of exploration. In this paper, we focus on this challenging but practical graph few-shot class-incremental learning (GFSCIL) problem and propose a novel method called Geometer. Instead of replacing and retraining the fully connected neural network classifer, Geometer predicts the label of a node by finding the nearest class prototype. Prototype is a vector representing a class in the metric space. With the pop-up of novel classes, Geometer learns and adjusts the attention-based prototypes by observing the geometric proximity, uniformity and separability. Teacher-student knowledge distillation and biased sampling are further introduced to mitigate catastrophic forgetting and unbalanced labeling problem respectively. Experimental results on four public datasets demonstrate that Geometer achieves a substantial improvement of 9.46% to 27.60% over state-of-the-art methods.

DeCOM: Decomposed Policy for Constrained Cooperative Multi-Agent Reinforcement Learning

In recent years, multi-agent reinforcement learning (MARL) has presented impressive performance in various applications. However, physical limitations, budget restrictions, and many other factors usually impose \textit{constraints} on a multi-agent system (MAS), which cannot be handled by traditional MARL frameworks. Specifically, this paper focuses on constrained MASes where agents work \textit{cooperatively} to maximize the expected team-average return under various constraints on expected team-average costs, and develops a \textit{constrained cooperative MARL} framework, named DeCOM, for such MASes. In particular, DeCOM decomposes the policy of each agent into two modules, which empowers information sharing among agents to achieve better cooperation. In addition, with such modularization, the training algorithm of DeCOM separates the original constrained optimization into an unconstrained optimization on reward and a constraints satisfaction problem on costs. DeCOM then iteratively solves these problems in a computationally efficient manner, which makes DeCOM highly scalable. We also provide theoretical guarantees on the convergence of DeCOM's policy update algorithm. Finally, we validate the effectiveness of DeCOM with various types of costs in both toy and large-scale (with 500 agents) environments.