VCORE: Variance-Controlled Optimization-based Reweighting for Chain-of-Thought Supervision

Supervised fine-tuning (SFT) on long chain-of-thought (CoT) trajectories has emerged as a crucial technique for enhancing the reasoning abilities of large language models (LLMs). However, the standard cross-entropy loss treats all tokens equally, ignoring their heterogeneous contributions across a reasoning trajectory. This uniform treatment leads to misallocated supervision and weak generalization, especially in complex, long-form reasoning tasks. To address this, we introduce \textbf{V}ariance-\textbf{C}ontrolled \textbf{O}ptimization-based \textbf{RE}weighting (VCORE), a principled framework that reformulates CoT supervision as a constrained optimization problem. By adopting an optimization-theoretic perspective, VCORE enables a principled and adaptive allocation of supervision across tokens, thereby aligning the training objective more closely with the goal of robust reasoning generalization. Empirical evaluations demonstrate that VCORE consistently outperforms existing token reweighting methods. Across both in-domain and out-of-domain settings, VCORE achieves substantial performance gains on mathematical and coding benchmarks, using models from the Qwen3 series (4B, 8B, 32B) and LLaMA-3.1-8B-Instruct. Moreover, we show that VCORE serves as a more effective initialization for subsequent reinforcement learning, establishing a stronger foundation for advancing the reasoning capabilities of LLMs. The Code will be released at https://github.com/coder-gx/VCORE.

From Parameters to Prompts: Understanding and Mitigating the Factuality Gap between Fine-Tuned LLMs

Factual knowledge extraction aims to explicitly extract knowledge parameterized in pre-trained language models for application in downstream tasks. While prior work has been investigating the impact of supervised fine-tuning data on the factuality of large language models (LLMs), its mechanism remains poorly understood. We revisit this impact through systematic experiments, with a particular focus on the factuality gap that arises when fine-tuning on known versus unknown knowledge. Our findings show that this gap can be mitigated at the inference stage, either under out-of-distribution (OOD) settings or by using appropriate in-context learning (ICL) prompts (i.e., few-shot learning and Chain of Thought (CoT)). We prove this phenomenon theoretically from the perspective of knowledge graphs, showing that the test-time prompt may diminish or even overshadow the impact of fine-tuning data and play a dominant role in knowledge extraction. Ultimately, our results shed light on the interaction between finetuning data and test-time prompt, demonstrating that ICL can effectively compensate for shortcomings in fine-tuning data, and highlighting the need to reconsider the use of ICL prompting as a means to evaluate the effectiveness of fine-tuning data selection methods.

Origin Tracer: A Method for Detecting LoRA Fine-Tuning Origins in LLMs

As large language models (LLMs) continue to advance, their deployment often involves fine-tuning to enhance performance on specific downstream tasks. However, this customization is sometimes accompanied by misleading claims about the origins, raising significant concerns about transparency and trust within the open-source community. Existing model verification techniques typically assess functional, representational, and weight similarities. However, these approaches often struggle against obfuscation techniques, such as permutations and scaling transformations. To address this limitation, we propose a novel detection method Origin-Tracer that rigorously determines whether a model has been fine-tuned from a specified base model. This method includes the ability to extract the LoRA rank utilized during the fine-tuning process, providing a more robust verification framework. This framework is the first to provide a formalized approach specifically aimed at pinpointing the sources of model fine-tuning. We empirically validated our method on thirty-one diverse open-source models under conditions that simulate real-world obfuscation scenarios. We empirically analyze the effectiveness of our framework and finally, discuss its limitations. The results demonstrate the effectiveness of our approach and indicate its potential to establish new benchmarks for model verification.

Archilles' Heel in Semi-open LLMs: Hiding Bottom against Recovery Attacks

Closed-source large language models deliver strong performance but have limited downstream customizability. Semi-open models, combining both closed-source and public layers, were introduced to improve customizability. However, parameters in the closed-source layers are found vulnerable to recovery attacks. In this paper, we explore the design of semi-open models with fewer closed-source layers, aiming to increase customizability while ensuring resilience to recovery attacks. We analyze the contribution of closed-source layer to the overall resilience and theoretically prove that in a deep transformer-based model, there exists a transition layer such that even small recovery errors in layers before this layer can lead to recovery failure. Building on this, we propose \textbf{SCARA}, a novel approach that keeps only a few bottom layers as closed-source. SCARA employs a fine-tuning-free metric to estimate the maximum number of layers that can be publicly accessible for customization. We apply it to five models (1.3B to 70B parameters) to construct semi-open models, validating their customizability on six downstream tasks and assessing their resilience against various recovery attacks on sixteen benchmarks. We compare SCARA to baselines and observe that it generally improves downstream customization performance and offers similar resilience with over \textbf{10} times fewer closed-source parameters. We empirically investigate the existence of transition layers, analyze the effectiveness of our scheme and finally discuss its limitations.

Temporal Generalization Estimation in Evolving Graphs

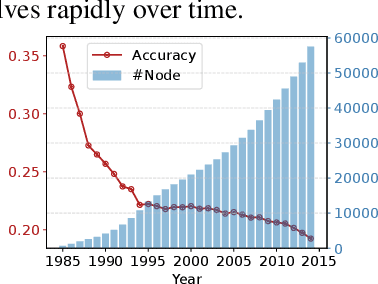
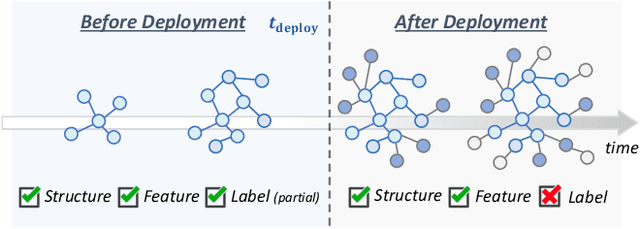
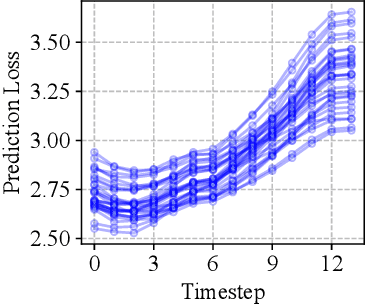
Graph Neural Networks (GNNs) are widely deployed in vast fields, but they often struggle to maintain accurate representations as graphs evolve. We theoretically establish a lower bound, proving that under mild conditions, representation distortion inevitably occurs over time. To estimate the temporal distortion without human annotation after deployment, one naive approach is to pre-train a recurrent model (e.g., RNN) before deployment and use this model afterwards, but the estimation is far from satisfactory. In this paper, we analyze the representation distortion from an information theory perspective, and attribute it primarily to inaccurate feature extraction during evolution. Consequently, we introduce Smart, a straightforward and effective baseline enhanced by an adaptive feature extractor through self-supervised graph reconstruction. In synthetic random graphs, we further refine the former lower bound to show the inevitable distortion over time and empirically observe that Smart achieves good estimation performance. Moreover, we observe that Smart consistently shows outstanding generalization estimation on four real-world evolving graphs. The ablation studies underscore the necessity of graph reconstruction. For example, on OGB-arXiv dataset, the estimation metric MAPE deteriorates from 2.19% to 8.00% without reconstruction.

AceMap: Knowledge Discovery through Academic Graph

The exponential growth of scientific literature requires effective management and extraction of valuable insights. While existing scientific search engines excel at delivering search results based on relational databases, they often neglect the analysis of collaborations between scientific entities and the evolution of ideas, as well as the in-depth analysis of content within scientific publications. The representation of heterogeneous graphs and the effective measurement, analysis, and mining of such graphs pose significant challenges. To address these challenges, we present AceMap, an academic system designed for knowledge discovery through academic graph. We present advanced database construction techniques to build the comprehensive AceMap database with large-scale academic publications that contain rich visual, textual, and numerical information. AceMap also employs innovative visualization, quantification, and analysis methods to explore associations and logical relationships among academic entities. AceMap introduces large-scale academic network visualization techniques centered on nebular graphs, providing a comprehensive view of academic networks from multiple perspectives. In addition, AceMap proposes a unified metric based on structural entropy to quantitatively measure the knowledge content of different academic entities. Moreover, AceMap provides advanced analysis capabilities, including tracing the evolution of academic ideas through citation relationships and concept co-occurrence, and generating concise summaries informed by this evolutionary process. In addition, AceMap uses machine reading methods to generate potential new ideas at the intersection of different fields. Exploring the integration of large language models and knowledge graphs is a promising direction for future research in idea evolution. Please visit \url{https://www.acemap.info} for further exploration.

Graph Out-of-Distribution Generalization with Controllable Data Augmentation

Graph Neural Network (GNN) has demonstrated extraordinary performance in classifying graph properties. However, due to the selection bias of training and testing data (e.g., training on small graphs and testing on large graphs, or training on dense graphs and testing on sparse graphs), distribution deviation is widespread. More importantly, we often observe \emph{hybrid structure distribution shift} of both scale and density, despite of one-sided biased data partition. The spurious correlations over hybrid distribution deviation degrade the performance of previous GNN methods and show large instability among different datasets. To alleviate this problem, we propose \texttt{OOD-GMixup} to jointly manipulate the training distribution with \emph{controllable data augmentation} in metric space. Specifically, we first extract the graph rationales to eliminate the spurious correlations due to irrelevant information. Secondly, we generate virtual samples with perturbation on graph rationale representation domain to obtain potential OOD training samples. Finally, we propose OOD calibration to measure the distribution deviation of virtual samples by leveraging Extreme Value Theory, and further actively control the training distribution by emphasizing the impact of virtual OOD samples. Extensive studies on several real-world datasets on graph classification demonstrate the superiority of our proposed method over state-of-the-art baselines.

Achieving Small Test Error in Mildly Overparameterized Neural Networks

Recent theoretical works on over-parameterized neural nets have focused on two aspects: optimization and generalization. Many existing works that study optimization and generalization together are based on neural tangent kernel and require a very large width. In this work, we are interested in the following question: for a binary classification problem with two-layer mildly over-parameterized ReLU network, can we find a point with small test error in polynomial time? We first show that the landscape of loss functions with explicit regularization has the following property: all local minima and certain other points which are only stationary in certain directions achieve small test error. We then prove that for convolutional neural nets, there is an algorithm which finds one of these points in polynomial time (in the input dimension and the number of data points). In addition, we prove that for a fully connected neural net, with an additional assumption on the data distribution, there is a polynomial time algorithm.

The Global Landscape of Neural Networks: An Overview

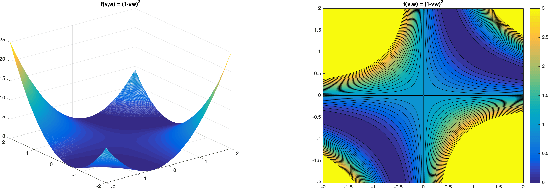
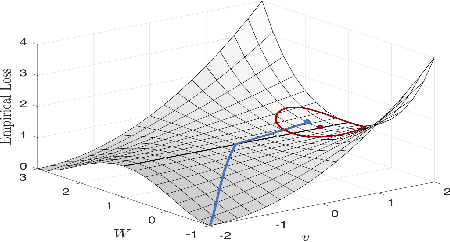
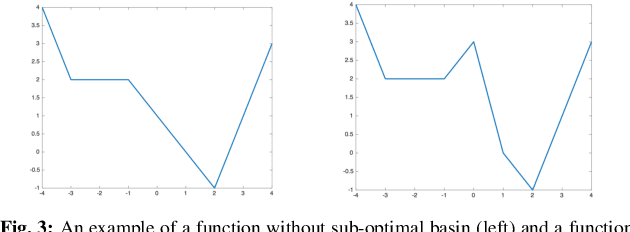
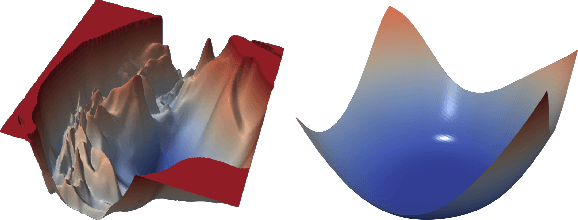
One of the major concerns for neural network training is that the non-convexity of the associated loss functions may cause bad landscape. The recent success of neural networks suggests that their loss landscape is not too bad, but what specific results do we know about the landscape? In this article, we review recent findings and results on the global landscape of neural networks. First, we point out that wide neural nets may have sub-optimal local minima under certain assumptions. Second, we discuss a few rigorous results on the geometric properties of wide networks such as "no bad basin", and some modifications that eliminate sub-optimal local minima and/or decreasing paths to infinity. Third, we discuss visualization and empirical explorations of the landscape for practical neural nets. Finally, we briefly discuss some convergence results and their relation to landscape results.

Revisiting Landscape Analysis in Deep Neural Networks: Eliminating Decreasing Paths to Infinity

Traditional landscape analysis of deep neural networks aims to show that no sub-optimal local minima exist in some appropriate sense. From this, one may be tempted to conclude that descent algorithms which escape saddle points will reach a good local minimum. However, basic optimization theory tell us that it is also possible for a descent algorithm to diverge to infinity if there are paths leading to infinity, along which the loss function decreases. It is not clear whether for non-linear neural networks there exists one setting that no bad local-min and no decreasing paths to infinity can be simultaneously achieved. In this paper, we give the first positive answer to this question. More specifically, for a large class of over-parameterized deep neural networks with appropriate regularizers, the loss function has no bad local minima and no decreasing paths to infinity. The key mathematical trick is to show that the set of regularizers which may be undesirable can be viewed as the image of a Lipschitz continuous mapping from a lower-dimensional Euclidean space to a higher-dimensional Euclidean space, and thus has zero measure.