PINN and GNN-based RF Map Construction for Wireless Communication Systems

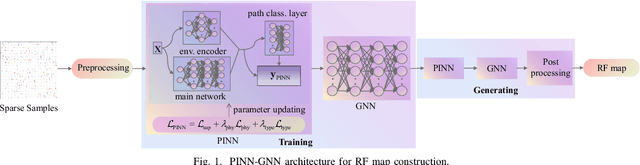
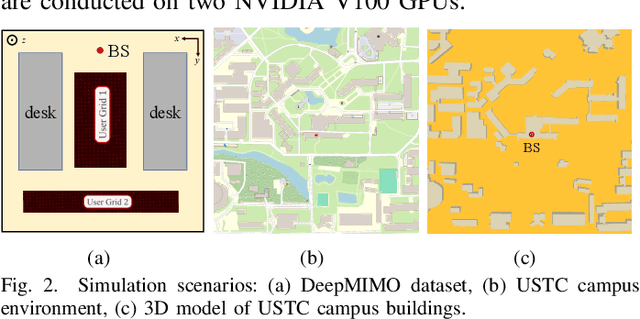
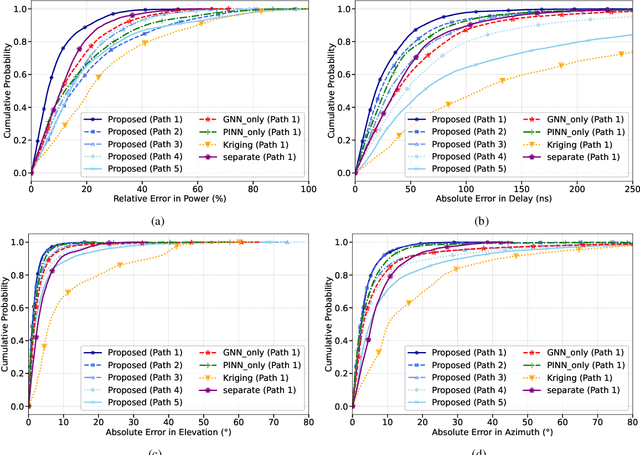
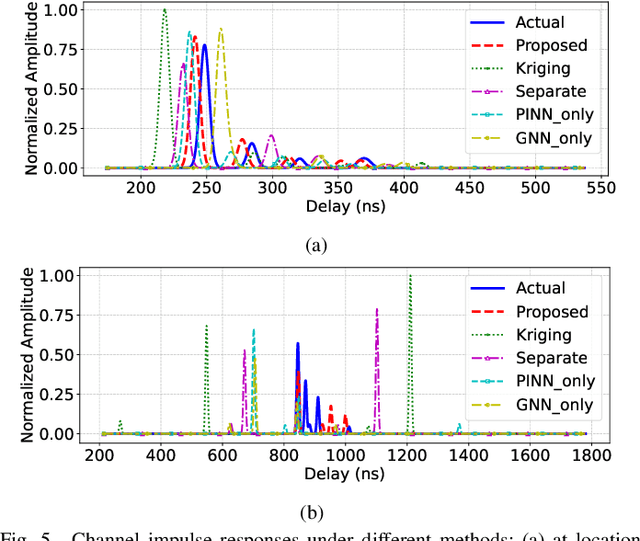
Radio frequency (RF) map is a promising technique for capturing the characteristics of multipath signal propagation, offering critical support for channel modeling, coverage analysis, and beamforming in wireless communication networks. This paper proposes a novel RF map construction method based on a combination of physics-informed neural network (PINN) and graph neural network (GNN). The PINN incorporates physical constraints derived from electromagnetic propagation laws to guide the learning process, while the GNN models spatial correlations among receiver locations. By parameterizing multipath signals into received power, delay, and angle of arrival (AoA), and integrating both physical priors and spatial dependencies, the proposed method achieves accurate prediction of multipath parameters. Experimental results demonstrate that the method enables high-precision RF map construction under sparse sampling conditions and delivers robust performance in both indoor and complex outdoor environments, outperforming baseline methods in terms of generalization and accuracy.

A Generalized Label Shift Perspective for Cross-Domain Gaze Estimation

Aiming to generalize the well-trained gaze estimation model to new target domains, Cross-domain Gaze Estimation (CDGE) is developed for real-world application scenarios. Existing CDGE methods typically extract the domain-invariant features to mitigate domain shift in feature space, which is proved insufficient by Generalized Label Shift (GLS) theory. In this paper, we introduce a novel GLS perspective to CDGE and modelize the cross-domain problem by label and conditional shift problem. A GLS correction framework is presented and a feasible realization is proposed, in which a importance reweighting strategy based on truncated Gaussian distribution is introduced to overcome the continuity challenges in label shift correction. To embed the reweighted source distribution to conditional invariant learning, we further derive a probability-aware estimation of conditional operator discrepancy. Extensive experiments on standard CDGE tasks with different backbone models validate the superior generalization capability across domain and applicability on various models of proposed method.

Sobolev Gradient Ascent for Optimal Transport: Barycenter Optimization and Convergence Analysis

This paper introduces a new constraint-free concave dual formulation for the Wasserstein barycenter. Tailoring the vanilla dual gradient ascent algorithm to the Sobolev geometry, we derive a scalable Sobolev gradient ascent (SGA) algorithm to compute the barycenter for input distributions supported on a regular grid. Despite the algorithmic simplicity, we provide a global convergence analysis that achieves the same rate as the classical subgradient descent methods for minimizing nonsmooth convex functions in the Euclidean space. A central feature of our SGA algorithm is that the computationally expensive $c$-concavity projection operator enforced on the Kantorovich dual potentials is unnecessary to guarantee convergence, leading to significant algorithmic and theoretical simplifications over all existing primal and dual methods for computing the exact barycenter. Our numerical experiments demonstrate the superior empirical performance of SGA over the existing optimal transport barycenter solvers.

Embedding Empirical Distributions for Computing Optimal Transport Maps

Distributional data have become increasingly prominent in modern signal processing, highlighting the necessity of computing optimal transport (OT) maps across multiple probability distributions. Nevertheless, recent studies on neural OT methods predominantly focused on the efficient computation of a single map between two distributions. To address this challenge, we introduce a novel approach to learning transport maps for new empirical distributions. Specifically, we employ the transformer architecture to produce embeddings from distributional data of varying length; these embeddings are then fed into a hypernetwork to generate neural OT maps. Various numerical experiments were conducted to validate the embeddings and the generated OT maps. The model implementation and the code are provided on https://github.com/jiangmingchen/HOTET.

Multi-Modal Foundation Models for Computational Pathology: A Survey

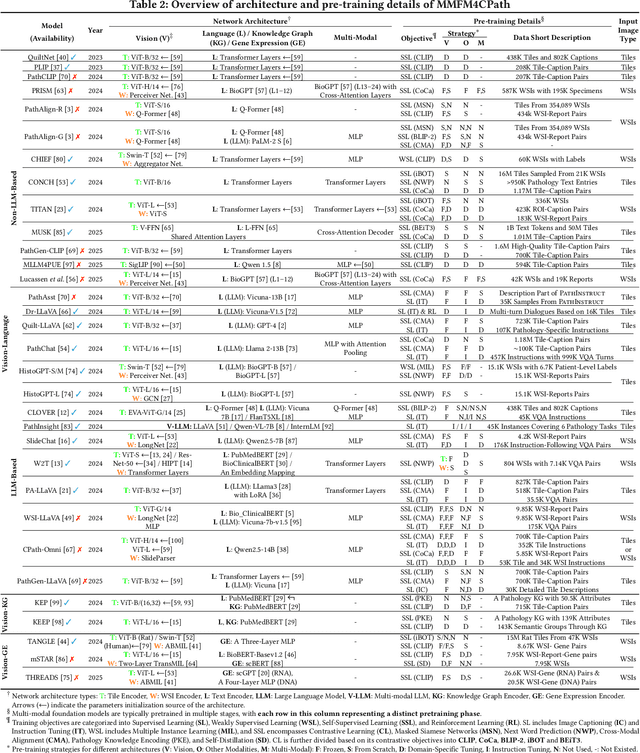
Foundation models have emerged as a powerful paradigm in computational pathology (CPath), enabling scalable and generalizable analysis of histopathological images. While early developments centered on uni-modal models trained solely on visual data, recent advances have highlighted the promise of multi-modal foundation models that integrate heterogeneous data sources such as textual reports, structured domain knowledge, and molecular profiles. In this survey, we provide a comprehensive and up-to-date review of multi-modal foundation models in CPath, with a particular focus on models built upon hematoxylin and eosin (H&E) stained whole slide images (WSIs) and tile-level representations. We categorize 32 state-of-the-art multi-modal foundation models into three major paradigms: vision-language, vision-knowledge graph, and vision-gene expression. We further divide vision-language models into non-LLM-based and LLM-based approaches. Additionally, we analyze 28 available multi-modal datasets tailored for pathology, grouped into image-text pairs, instruction datasets, and image-other modality pairs. Our survey also presents a taxonomy of downstream tasks, highlights training and evaluation strategies, and identifies key challenges and future directions. We aim for this survey to serve as a valuable resource for researchers and practitioners working at the intersection of pathology and AI.

High-fidelity Multiphysics Modelling for Rapid Predictions Using Physics-informed Parallel Neural Operator

Modelling complex multiphysics systems governed by nonlinear and strongly coupled partial differential equations (PDEs) is a cornerstone in computational science and engineering. However, it remains a formidable challenge for traditional numerical solvers due to high computational cost, making them impractical for large-scale applications. Neural operators' reliance on data-driven training limits their applicability in real-world scenarios, as data is often scarce or expensive to obtain. Here, we propose a novel paradigm, physics-informed parallel neural operator (PIPNO), a scalable and unsupervised learning framework that enables data-free PDE modelling by leveraging only governing physical laws. The parallel kernel integration design, incorporating ensemble learning, significantly enhances both compatibility and computational efficiency, enabling scalable operator learning for nonlinear and strongly coupled PDEs. PIPNO efficiently captures nonlinear operator mappings across diverse physics, including geotechnical engineering, material science, electromagnetism, quantum mechanics, and fluid dynamics. The proposed method achieves high-fidelity and rapid predictions, outperforming existing operator learning approaches in modelling nonlinear and strongly coupled multiphysics systems. Therefore, PIPNO offers a powerful alternative to conventional solvers, broadening the applicability of neural operators for multiphysics modelling while ensuring efficiency, robustness, and scalability.

Convergence Analysis of the Wasserstein Proximal Algorithm beyond Geodesic Convexity

The proximal algorithm is a powerful tool to minimize nonlinear and nonsmooth functionals in a general metric space. Motivated by the recent progress in studying the training dynamics of the noisy gradient descent algorithm on two-layer neural networks in the mean-field regime, we provide in this paper a simple and self-contained analysis for the convergence of the general-purpose Wasserstein proximal algorithm without assuming geodesic convexity of the objective functional. Under a natural Wasserstein analog of the Euclidean Polyak-{\L}ojasiewicz inequality, we establish that the proximal algorithm achieves an unbiased and linear convergence rate. Our convergence rate improves upon existing rates of the proximal algorithm for solving Wasserstein gradient flows under strong geodesic convexity. We also extend our analysis to the inexact proximal algorithm for geodesically semiconvex objectives. In our numerical experiments, proximal training demonstrates a faster convergence rate than the noisy gradient descent algorithm on mean-field neural networks.

Optimal Transport Barycenter via Nonconvex-Concave Minimax Optimization

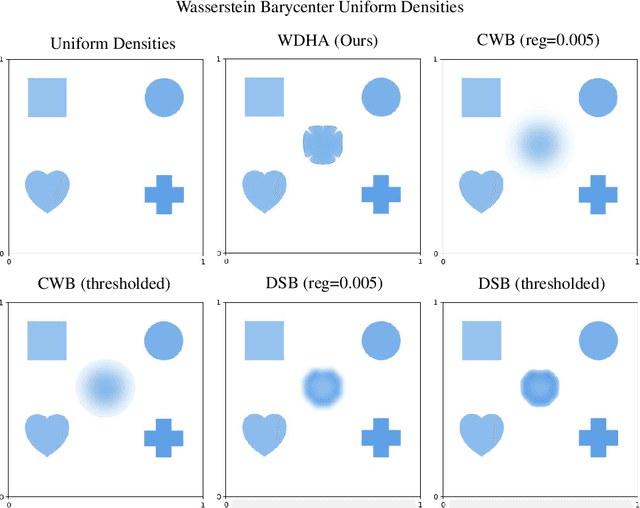
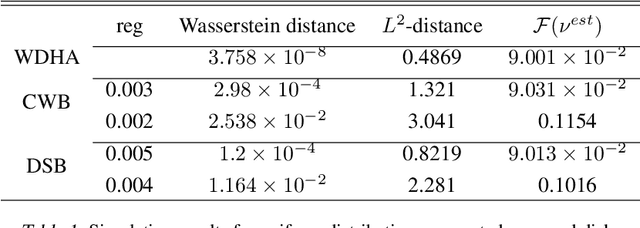
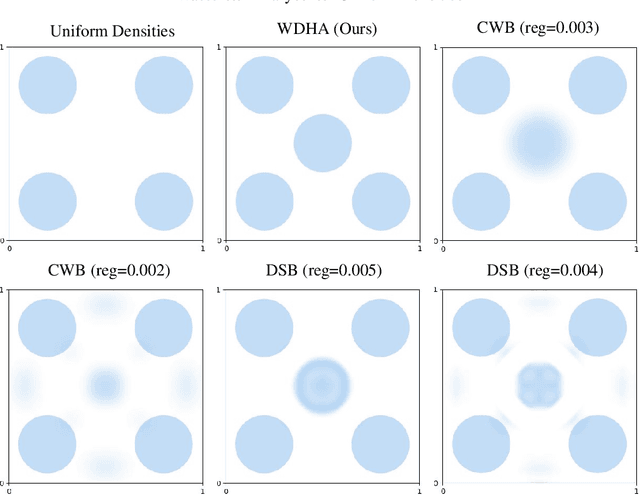
The optimal transport barycenter (a.k.a. Wasserstein barycenter) is a fundamental notion of averaging that extends from the Euclidean space to the Wasserstein space of probability distributions. Computation of the unregularized barycenter for discretized probability distributions on point clouds is a challenging task when the domain dimension $d > 1$. Most practical algorithms for approximating the barycenter problem are based on entropic regularization. In this paper, we introduce a nearly linear time $O(m \log{m})$ and linear space complexity $O(m)$ primal-dual algorithm, the Wasserstein-Descent $\dot{\mathbb{H}}^1$-Ascent (WDHA) algorithm, for computing the exact barycenter when the input probability density functions are discretized on an $m$-point grid. The key success of the WDHA algorithm hinges on alternating between two different yet closely related Wasserstein and Sobolev optimization geometries for the primal barycenter and dual Kantorovich potential subproblems. Under reasonable assumptions, we establish the convergence rate and iteration complexity of WDHA to its stationary point when the step size is appropriately chosen. Superior computational efficacy, scalability, and accuracy over the existing Sinkhorn-type algorithms are demonstrated on high-resolution (e.g., $1024 \times 1024$ images) 2D synthetic and real data.

Large Language Model is Secretly a Protein Sequence Optimizer

We consider the protein sequence engineering problem, which aims to find protein sequences with high fitness levels, starting from a given wild-type sequence. Directed evolution has been a dominating paradigm in this field which has an iterative process to generate variants and select via experimental feedback. We demonstrate large language models (LLMs), despite being trained on massive texts, are secretly protein sequence optimizers. With a directed evolutionary method, LLM can perform protein engineering through Pareto and experiment-budget constrained optimization, demonstrating success on both synthetic and experimental fitness landscapes.

MADGEN -- Mass-Spec attends to De Novo Molecular generation

The annotation (assigning structural chemical identities) of MS/MS spectra remains a significant challenge due to the enormous molecular diversity in biological samples and the limited scope of reference databases. Currently, the vast majority of spectral measurements remain in the "dark chemical space" without structural annotations. To improve annotation, we propose MADGEN (Mass-spec Attends to De Novo Molecular GENeration), a scaffold-based method for de novo molecular structure generation guided by mass spectrometry data. MADGEN operates in two stages: scaffold retrieval and spectra-conditioned molecular generation starting with the scaffold. In the first stage, given an MS/MS spectrum, we formulate scaffold retrieval as a ranking problem and employ contrastive learning to align mass spectra with candidate molecular scaffolds. In the second stage, starting from the retrieved scaffold, we employ the MS/MS spectrum to guide an attention-based generative model to generate the final molecule. Our approach constrains the molecular generation search space, reducing its complexity and improving generation accuracy. We evaluate MADGEN on three datasets (NIST23, CANOPUS, and MassSpecGym) and evaluate MADGEN's performance with a predictive scaffold retriever and with an oracle retriever. We demonstrate the effectiveness of using attention to integrate spectral information throughout the generation process to achieve strong results with the oracle retriever.