Sobolev Gradient Ascent for Optimal Transport: Barycenter Optimization and Convergence Analysis

This paper introduces a new constraint-free concave dual formulation for the Wasserstein barycenter. Tailoring the vanilla dual gradient ascent algorithm to the Sobolev geometry, we derive a scalable Sobolev gradient ascent (SGA) algorithm to compute the barycenter for input distributions supported on a regular grid. Despite the algorithmic simplicity, we provide a global convergence analysis that achieves the same rate as the classical subgradient descent methods for minimizing nonsmooth convex functions in the Euclidean space. A central feature of our SGA algorithm is that the computationally expensive $c$-concavity projection operator enforced on the Kantorovich dual potentials is unnecessary to guarantee convergence, leading to significant algorithmic and theoretical simplifications over all existing primal and dual methods for computing the exact barycenter. Our numerical experiments demonstrate the superior empirical performance of SGA over the existing optimal transport barycenter solvers.

Optimal Transport Barycenter via Nonconvex-Concave Minimax Optimization

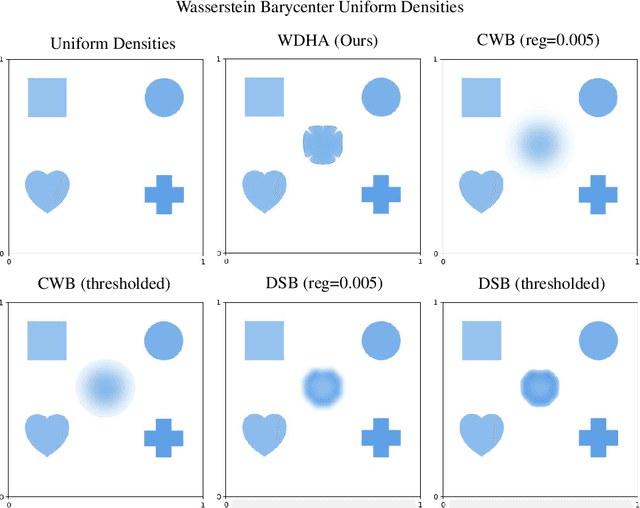
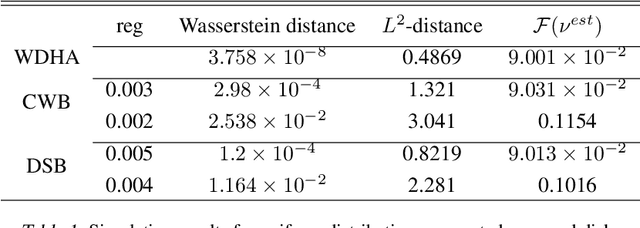
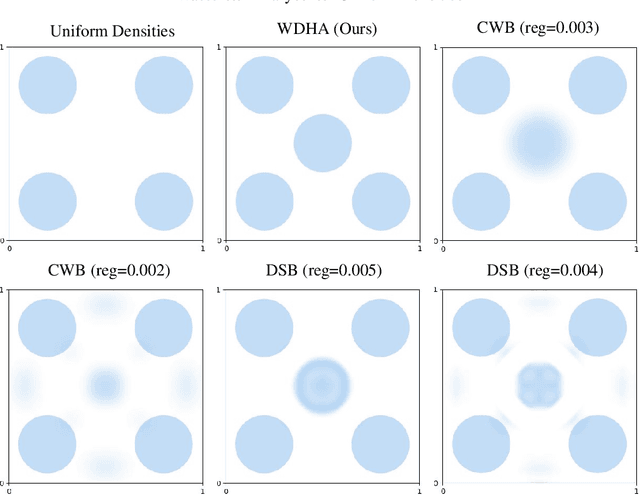
The optimal transport barycenter (a.k.a. Wasserstein barycenter) is a fundamental notion of averaging that extends from the Euclidean space to the Wasserstein space of probability distributions. Computation of the unregularized barycenter for discretized probability distributions on point clouds is a challenging task when the domain dimension $d > 1$. Most practical algorithms for approximating the barycenter problem are based on entropic regularization. In this paper, we introduce a nearly linear time $O(m \log{m})$ and linear space complexity $O(m)$ primal-dual algorithm, the Wasserstein-Descent $\dot{\mathbb{H}}^1$-Ascent (WDHA) algorithm, for computing the exact barycenter when the input probability density functions are discretized on an $m$-point grid. The key success of the WDHA algorithm hinges on alternating between two different yet closely related Wasserstein and Sobolev optimization geometries for the primal barycenter and dual Kantorovich potential subproblems. Under reasonable assumptions, we establish the convergence rate and iteration complexity of WDHA to its stationary point when the step size is appropriately chosen. Superior computational efficacy, scalability, and accuracy over the existing Sinkhorn-type algorithms are demonstrated on high-resolution (e.g., $1024 \times 1024$ images) 2D synthetic and real data.