A Generalized Label Shift Perspective for Cross-Domain Gaze Estimation

Aiming to generalize the well-trained gaze estimation model to new target domains, Cross-domain Gaze Estimation (CDGE) is developed for real-world application scenarios. Existing CDGE methods typically extract the domain-invariant features to mitigate domain shift in feature space, which is proved insufficient by Generalized Label Shift (GLS) theory. In this paper, we introduce a novel GLS perspective to CDGE and modelize the cross-domain problem by label and conditional shift problem. A GLS correction framework is presented and a feasible realization is proposed, in which a importance reweighting strategy based on truncated Gaussian distribution is introduced to overcome the continuity challenges in label shift correction. To embed the reweighted source distribution to conditional invariant learning, we further derive a probability-aware estimation of conditional operator discrepancy. Extensive experiments on standard CDGE tasks with different backbone models validate the superior generalization capability across domain and applicability on various models of proposed method.

Soft-Masked Semi-Dual Optimal Transport for Partial Domain Adaptation

Visual domain adaptation aims to learn discriminative and domain-invariant representation for an unlabeled target domain by leveraging knowledge from a labeled source domain. Partial domain adaptation (PDA) is a general and practical scenario in which the target label space is a subset of the source one. The challenges of PDA exist due to not only domain shift but also the non-identical label spaces of domains. In this paper, a Soft-masked Semi-dual Optimal Transport (SSOT) method is proposed to deal with the PDA problem. Specifically, the class weights of domains are estimated, and then a reweighed source domain is constructed, which is favorable in conducting class-conditional distribution matching with the target domain. A soft-masked transport distance matrix is constructed by category predictions, which will enhance the class-oriented representation ability of optimal transport in the shared feature space. To deal with large-scale optimal transport problems, the semi-dual formulation of the entropy-regularized Kantorovich problem is employed since it can be optimized by gradient-based algorithms. Further, a neural network is exploited to approximate the Kantorovich potential due to its strong fitting ability. This network parametrization also allows the generalization of the dual variable outside the supports of the input distribution. The SSOT model is built upon neural networks, which can be optimized alternately in an end-to-end manner. Extensive experiments are conducted on four benchmark datasets to demonstrate the effectiveness of SSOT.

A Physics-preserved Transfer Learning Method for Differential Equations

While data-driven methods such as neural operator have achieved great success in solving differential equations (DEs), they suffer from domain shift problems caused by different learning environments (with data bias or equation changes), which can be alleviated by transfer learning (TL). However, existing TL methods adopted in DEs problems lack either generalizability in general DEs problems or physics preservation during training. In this work, we focus on a general transfer learning method that adaptively correct the domain shift and preserve physical information. Mathematically, we characterize the data domain as product distribution and the essential problems as distribution bias and operator bias. A Physics-preserved Optimal Tensor Transport (POTT) method that simultaneously admits generalizability to common DEs and physics preservation of specific problem is proposed to adapt the data-driven model to target domain utilizing the push-forward distribution induced by the POTT map. Extensive experiments demonstrate the superior performance, generalizability and physics preservation of the proposed POTT method.

COD: Learning Conditional Invariant Representation for Domain Adaptation Regression

Aiming to generalize the label knowledge from a source domain with continuous outputs to an unlabeled target domain, Domain Adaptation Regression (DAR) is developed for complex practical learning problems. However, due to the continuity problem in regression, existing conditional distribution alignment theory and methods with discrete prior, which are proven to be effective in classification settings, are no longer applicable. In this work, focusing on the feasibility problems in DAR, we establish the sufficiency theory for the regression model, which shows the generalization error can be sufficiently dominated by the cross-domain conditional discrepancy. Further, to characterize conditional discrepancy with continuous conditioning variable, a novel Conditional Operator Discrepancy (COD) is proposed, which admits the metric property on conditional distributions via the kernel embedding theory. Finally, to minimize the discrepancy, a COD-based conditional invariant representation learning model is proposed, and the reformulation is derived to show that reasonable modifications on moment statistics can further improve the discriminability of the adaptation model. Extensive experiments on standard DAR datasets verify the validity of theoretical results and the superiority over SOTA DAR methods.

When Invariant Representation Learning Meets Label Shift: Insufficiency and Theoretical Insights

As a crucial step toward real-world learning scenarios with changing environments, dataset shift theory and invariant representation learning algorithm have been extensively studied to relax the identical distribution assumption in classical learning setting. Among the different assumptions on the essential of shifting distributions, generalized label shift (GLS) is the latest developed one which shows great potential to deal with the complex factors within the shift. In this paper, we aim to explore the limitations of current dataset shift theory and algorithm, and further provide new insights by presenting a comprehensive understanding of GLS. From theoretical aspect, two informative generalization bounds are derived, and the GLS learner is proved to be sufficiently close to optimal target model from the Bayesian perspective. The main results show the insufficiency of invariant representation learning, and prove the sufficiency and necessity of GLS correction for generalization, which provide theoretical supports and innovations for exploring generalizable model under dataset shift. From methodological aspect, we provide a unified view of existing shift correction frameworks, and propose a kernel embedding-based correction algorithm (KECA) to minimize the generalization error and achieve successful knowledge transfer. Both theoretical results and extensive experiment evaluations demonstrate the sufficiency and necessity of GLS correction for addressing dataset shift and the superiority of proposed algorithm.

Adaptive Texture Filtering for Single-Domain Generalized Segmentation

Domain generalization in semantic segmentation aims to alleviate the performance degradation on unseen domains through learning domain-invariant features. Existing methods diversify images in the source domain by adding complex or even abnormal textures to reduce the sensitivity to domain specific features. However, these approaches depend heavily on the richness of the texture bank, and training them can be time-consuming. In contrast to importing textures arbitrarily or augmenting styles randomly, we focus on the single source domain itself to achieve generalization. In this paper, we present a novel adaptive texture filtering mechanism to suppress the influence of texture without using augmentation, thus eliminating the interference of domain-specific features. Further, we design a hierarchical guidance generalization network equipped with structure-guided enhancement modules, which purpose is to learn the domain-invariant generalized knowledge. Extensive experiments together with ablation studies on widely-used datasets are conducted to verify the effectiveness of the proposed model, and reveal its superiority over other state-of-the-art alternatives.

Bures Joint Distribution Alignment with Dynamic Margin for Unsupervised Domain Adaptation

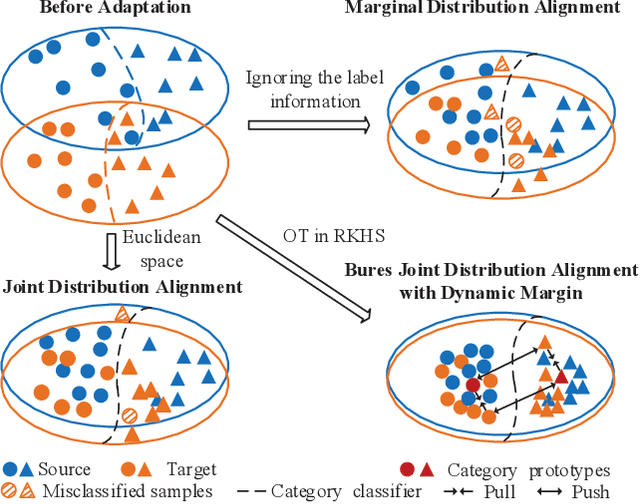
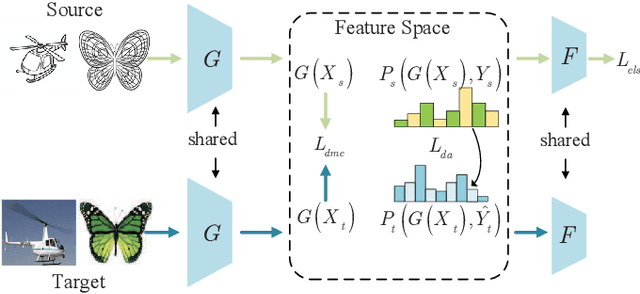
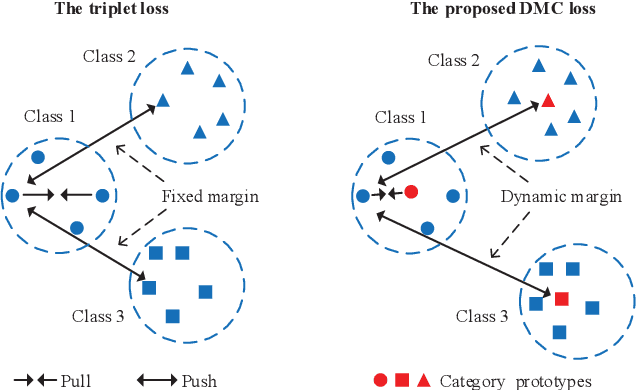
Unsupervised domain adaptation (UDA) is one of the prominent tasks of transfer learning, and it provides an effective approach to mitigate the distribution shift between the labeled source domain and the unlabeled target domain. Prior works mainly focus on aligning the marginal distributions or the estimated class-conditional distributions. However, the joint dependency among the feature and the label is crucial for the adaptation task and is not fully exploited. To address this problem, we propose the Bures Joint Distribution Alignment (BJDA) algorithm which directly models the joint distribution shift based on the optimal transport theory in the infinite-dimensional kernel spaces. Specifically, we propose a novel alignment loss term that minimizes the kernel Bures-Wasserstein distance between the joint distributions. Technically, BJDA can effectively capture the nonlinear structures underlying the data. In addition, we introduce a dynamic margin in contrastive learning phase to flexibly characterize the class separability and improve the discriminative ability of representations. It also avoids the cross-validation procedure to determine the margin parameter in traditional triplet loss based methods. Extensive experiments show that BJDA is very effective for the UDA tasks, as it outperforms state-of-the-art algorithms in most experimental settings. In particular, BJDA improves the average accuracy of UDA tasks by 2.8% on Adaptiope, 1.4% on Office-Caltech10, and 1.1% on ImageCLEF-DA.

Generalized Label Shift Correction via Minimum Uncertainty Principle: Theory and Algorithm

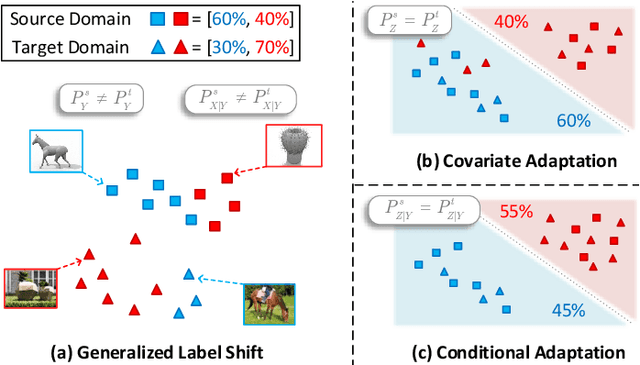
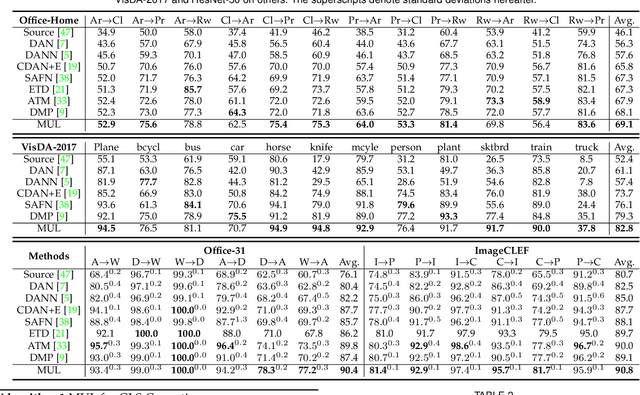
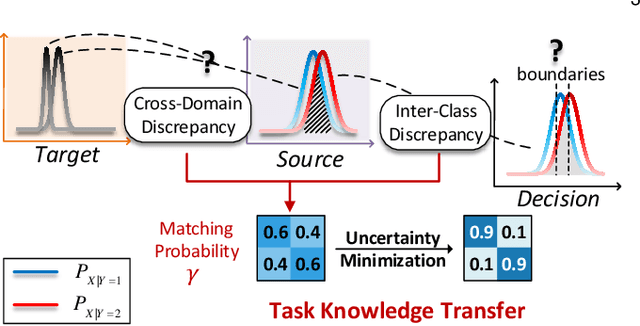
As a fundamental problem in machine learning, dataset shift induces a paradigm to learn and transfer knowledge under changing environment. Previous methods assume the changes are induced by covariate, which is less practical for complex real-world data. We consider the Generalized Label Shift (GLS), which provides an interpretable insight into the learning and transfer of desirable knowledge. Current GLS methods: 1) are not well-connected with the statistical learning theory; 2) usually assume the shifting conditional distributions will be matched with an implicit transformation, but its explicit modeling is unexplored. In this paper, we propose a conditional adaptation framework to deal with these challenges. From the perspective of learning theory, we prove that the generalization error of conditional adaptation is lower than previous covariate adaptation. Following the theoretical results, we propose the minimum uncertainty principle to learn conditional invariant transformation via discrepancy optimization. Specifically, we propose the \textit{conditional metric operator} on Hilbert space to characterize the distinctness of conditional distributions. For finite observations, we prove that the empirical estimation is always well-defined and will converge to underlying truth as sample size increases. The results of extensive experiments demonstrate that the proposed model achieves competitive performance under different GLS scenarios.

SPNet: A novel deep neural network for retinal vessel segmentation based on shared decoder and pyramid-like loss

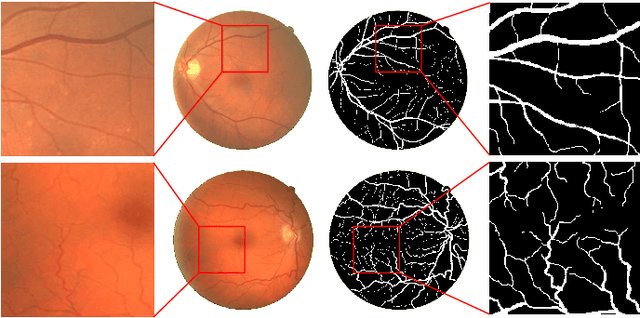
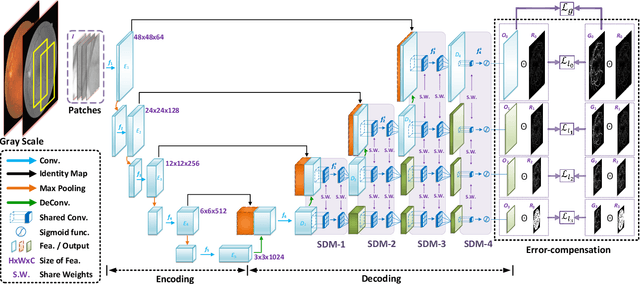
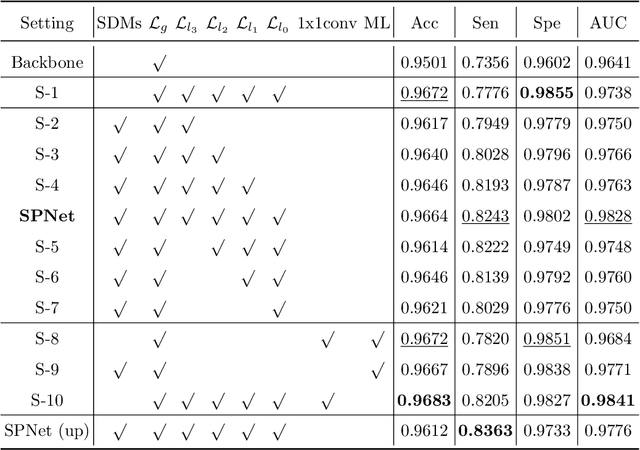
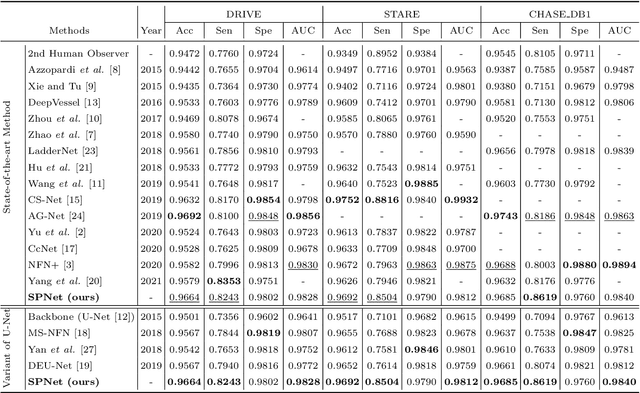
Segmentation of retinal vessel images is critical to the diagnosis of retinopathy. Recently, convolutional neural networks have shown significant ability to extract the blood vessel structure. However, it remains challenging to refined segmentation for the capillaries and the edges of retinal vessels due to thickness inconsistencies and blurry boundaries. In this paper, we propose a novel deep neural network for retinal vessel segmentation based on shared decoder and pyramid-like loss (SPNet) to address the above problems. Specifically, we introduce a decoder-sharing mechanism to capture multi-scale semantic information, where feature maps at diverse scales are decoded through a sequence of weight-sharing decoder modules. Also, to strengthen characterization on the capillaries and the edges of blood vessels, we define a residual pyramid architecture which decomposes the spatial information in the decoding phase. A pyramid-like loss function is designed to compensate possible segmentation errors progressively. Experimental results on public benchmarks show that the proposed method outperforms the backbone network and the state-of-the-art methods, especially in the regions of the capillaries and the vessel contours. In addition, performances on cross-datasets verify that SPNet shows stronger generalization ability.

Geometry-Aware Unsupervised Domain Adaptation

Unsupervised Domain Adaptation (UDA) aims to transfer the knowledge from the labeled source domain to the unlabeled target domain in the presence of dataset shift. Most existing methods cannot address the domain alignment and class discrimination well, which may distort the intrinsic data structure for downstream tasks (e.g., classification). To this end, we propose a novel geometry-aware model to learn the transferability and discriminability simultaneously via nuclear norm optimization. We introduce the domain coherence and class orthogonality for UDA from the perspective of subspace geometry. The domain coherence will ensure the model has a larger capacity for learning separable representations, and class orthogonality will minimize the correlation between clusters to alleviate the misalignment. So, they are consistent and can benefit from each other. Besides, we provide a theoretical insight into the norm-based learning literature in UDA, which ensures the interpretability of our model. We show that the norms of domains and clusters are expected to be larger and smaller to enhance the transferability and discriminability, respectively. Extensive experimental results on standard UDA datasets demonstrate the effectiveness of our theory and model.