DP-PCA: Statistically Optimal and Differentially Private PCA

We study the canonical statistical task of computing the principal component from $n$ i.i.d.~data in $d$ dimensions under $(\varepsilon,\delta)$-differential privacy. Although extensively studied in literature, existing solutions fall short on two key aspects: ($i$) even for Gaussian data, existing private algorithms require the number of samples $n$ to scale super-linearly with $d$, i.e., $n=\Omega(d^{3/2})$, to obtain non-trivial results while non-private PCA requires only $n=O(d)$, and ($ii$) existing techniques suffer from a non-vanishing error even when the randomness in each data point is arbitrarily small. We propose DP-PCA, which is a single-pass algorithm that overcomes both limitations. It is based on a private minibatch gradient ascent method that relies on {\em private mean estimation}, which adds minimal noise required to ensure privacy by adapting to the variance of a given minibatch of gradients. For sub-Gaussian data, we provide nearly optimal statistical error rates even for $n=\tilde O(d)$. Furthermore, we provide a lower bound showing that sub-Gaussian style assumption is necessary in obtaining the optimal error rate.

A Top-Down Approach to Hierarchically Coherent Probabilistic Forecasting

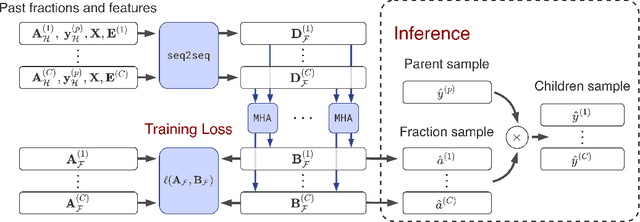
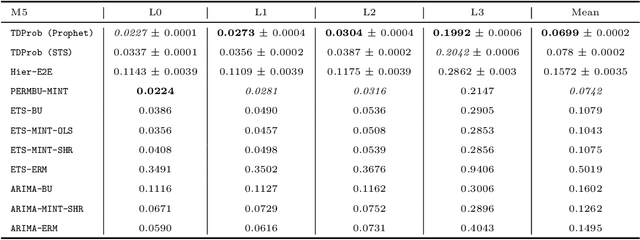
Hierarchical forecasting is a key problem in many practical multivariate forecasting applications - the goal is to obtain coherent predictions for a large number of correlated time series that are arranged in a pre-specified tree hierarchy. In this paper, we present a probabilistic top-down approach to hierarchical forecasting that uses a novel attention-based RNN model to learn the distribution of the proportions according to which each parent prediction is split among its children nodes at any point in time. These probabilistic proportions are then coupled with an independent univariate probabilistic forecasting model (such as Prophet or STS) for the root time series. The resulting forecasts are computed in a top-down fashion and are naturally coherent, and also support probabilistic predictions over all time series in the hierarchy. We provide theoretical justification for the superiority of our top-down approach compared to traditional bottom-up hierarchical modeling. Finally, we experiment on three public datasets and demonstrate significantly improved probabilistic forecasts, compared to state-of-the-art probabilistic hierarchical models.

Differential privacy and robust statistics in high dimensions

We introduce a universal framework for characterizing the statistical efficiency of a statistical estimation problem with differential privacy guarantees. Our framework, which we call High-dimensional Propose-Test-Release (HPTR), builds upon three crucial components: the exponential mechanism, robust statistics, and the Propose-Test-Release mechanism. Gluing all these together is the concept of resilience, which is central to robust statistical estimation. Resilience guides the design of the algorithm, the sensitivity analysis, and the success probability analysis of the test step in Propose-Test-Release. The key insight is that if we design an exponential mechanism that accesses the data only via one-dimensional robust statistics, then the resulting local sensitivity can be dramatically reduced. Using resilience, we can provide tight local sensitivity bounds. These tight bounds readily translate into near-optimal utility guarantees in several cases. We give a general recipe for applying HPTR to a given instance of a statistical estimation problem and demonstrate it on canonical problems of mean estimation, linear regression, covariance estimation, and principal component analysis. We introduce a general utility analysis technique that proves that HPTR nearly achieves the optimal sample complexity under several scenarios studied in the literature.

Fisher-Pitman permutation tests based on nonparametric Poisson mixtures with application to single cell genomics

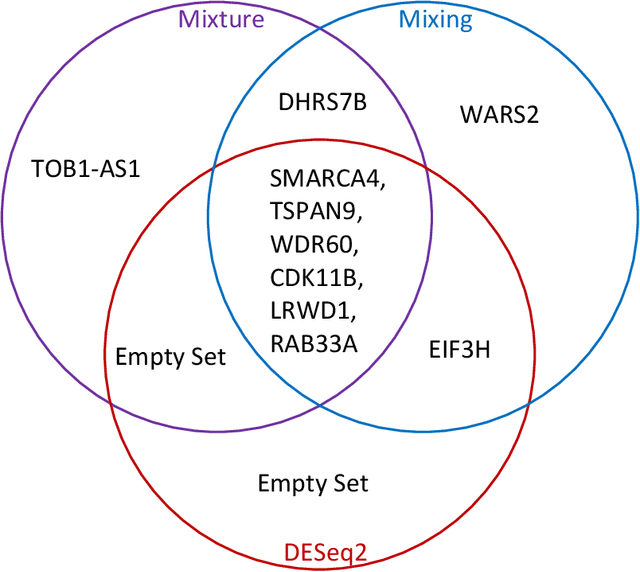
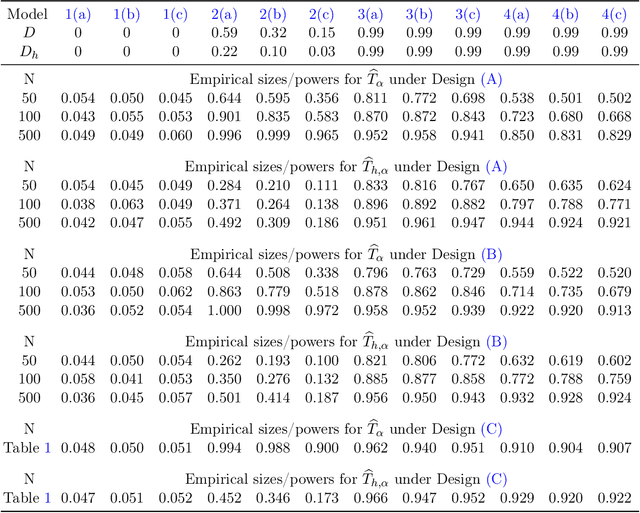
This paper investigates the theoretical and empirical performance of Fisher-Pitman-type permutation tests for assessing the equality of unknown Poisson mixture distributions. Building on nonparametric maximum likelihood estimators (NPMLEs) of the mixing distribution, these tests are theoretically shown to be able to adapt to complicated unspecified structures of count data and also consistent against their corresponding ANOVA-type alternatives; the latter is a result in parallel to classic claims made by Robinson (Robinson, 1973). The studied methods are then applied to a single-cell RNA-seq data obtained from different cell types from brain samples of autism subjects and healthy controls; empirically, they unveil genes that are differentially expressed between autism and control subjects yet are missed using common tests. For justifying their use, rate optimality of NPMLEs is also established in settings similar to nonparametric Gaussian (Wu and Yang, 2020a) and binomial mixtures (Tian et al., 2017; Vinayak et al., 2019).

SPECTRE: Defending Against Backdoor Attacks Using Robust Statistics

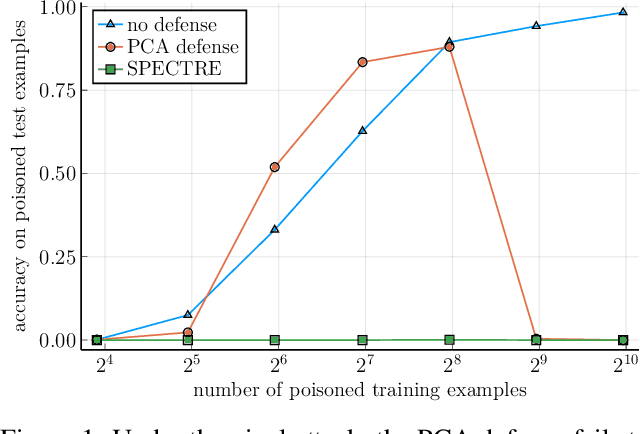
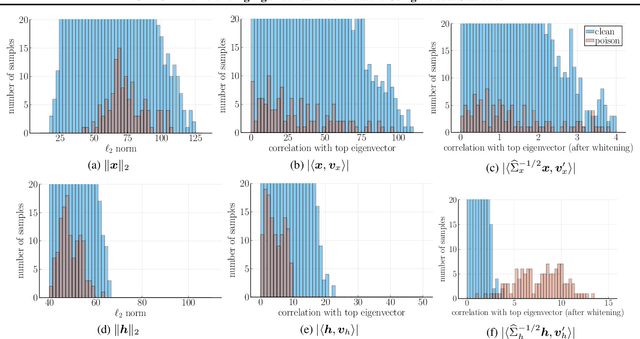
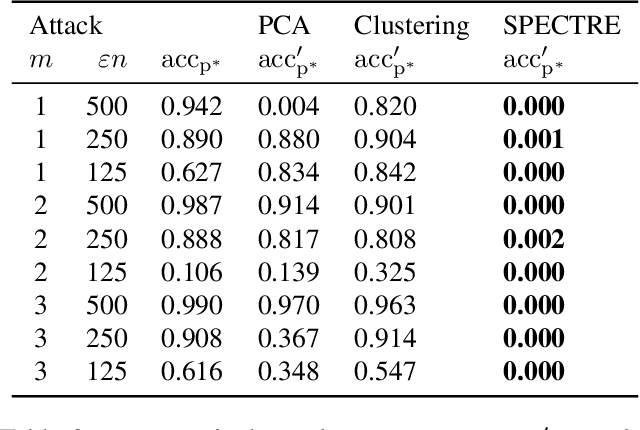
Modern machine learning increasingly requires training on a large collection of data from multiple sources, not all of which can be trusted. A particularly concerning scenario is when a small fraction of poisoned data changes the behavior of the trained model when triggered by an attacker-specified watermark. Such a compromised model will be deployed unnoticed as the model is accurate otherwise. There have been promising attempts to use the intermediate representations of such a model to separate corrupted examples from clean ones. However, these defenses work only when a certain spectral signature of the poisoned examples is large enough for detection. There is a wide range of attacks that cannot be protected against by the existing defenses. We propose a novel defense algorithm using robust covariance estimation to amplify the spectral signature of corrupted data. This defense provides a clean model, completely removing the backdoor, even in regimes where previous methods have no hope of detecting the poisoned examples. Code and pre-trained models are available at https://github.com/SewoongLab/spectre-defense .

Robust and Differentially Private Mean Estimation

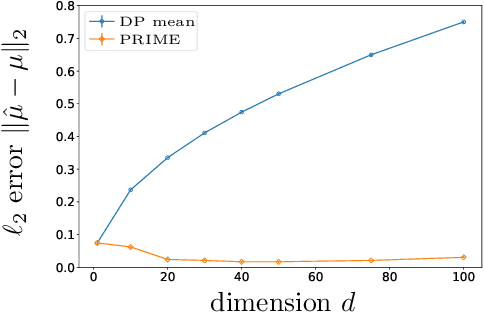
Differential privacy has emerged as a standard requirement in a variety of applications ranging from the U.S. Census to data collected in commercial devices, initiating an extensive line of research in accurately and privately releasing statistics of a database. An increasing number of such databases consist of data from multiple sources, not all of which can be trusted. This leaves existing private analyses vulnerable to attacks by an adversary who injects corrupted data. Despite the significance of designing algorithms that guarantee privacy and robustness (to a fraction of data being corrupted) simultaneously, even the simplest questions remain open. For the canonical problem of estimating the mean from i.i.d. samples, we introduce the first efficient algorithm that achieves both privacy and robustness for a wide range of distributions. This achieves optimal accuracy matching the known lower bounds for robustness, but the sample complexity has a factor of $d^{1/2}$ gap from known lower bounds. We further show that this gap is due to the computational efficiency; we introduce the first family of algorithms that close this gap but takes exponential time. The innovation is in exploiting resilience (a key property in robust estimation) to adaptively bound the sensitivity and improve privacy.

Online Model Selection for Reinforcement Learning with Function Approximation

Deep reinforcement learning has achieved impressive successes yet often requires a very large amount of interaction data. This result is perhaps unsurprising, as using complicated function approximation often requires more data to fit, and early theoretical results on linear Markov decision processes provide regret bounds that scale with the dimension of the linear approximation. Ideally, we would like to automatically identify the minimal dimension of the approximation that is sufficient to encode an optimal policy. Towards this end, we consider the problem of model selection in RL with function approximation, given a set of candidate RL algorithms with known regret guarantees. The learner's goal is to adapt to the complexity of the optimal algorithm without knowing it \textit{a priori}. We present a meta-algorithm that successively rejects increasingly complex models using a simple statistical test. Given at least one candidate that satisfies realizability, we prove the meta-algorithm adapts to the optimal complexity with $\tilde{O}(L^{5/6} T^{2/3})$ regret compared to the optimal candidate's $\tilde{O}(\sqrt T)$ regret, where $T$ is the number of episodes and $L$ is the number of algorithms. The dimension and horizon dependencies remain optimal with respect to the best candidate, and our meta-algorithmic approach is flexible to incorporate multiple candidate algorithms and models. Finally, we show that the meta-algorithm automatically admits significantly improved instance-dependent regret bounds that depend on the gaps between the maximal values attainable by the candidates.

Robust Meta-learning for Mixed Linear Regression with Small Batches

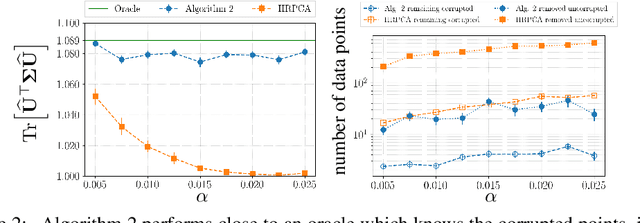
A common challenge faced in practical supervised learning, such as medical image processing and robotic interactions, is that there are plenty of tasks but each task cannot afford to collect enough labeled examples to be learned in isolation. However, by exploiting the similarities across those tasks, one can hope to overcome such data scarcity. Under a canonical scenario where each task is drawn from a mixture of k linear regressions, we study a fundamental question: can abundant small-data tasks compensate for the lack of big-data tasks? Existing second moment based approaches show that such a trade-off is efficiently achievable, with the help of medium-sized tasks with $\Omega(k^{1/2})$ examples each. However, this algorithm is brittle in two important scenarios. The predictions can be arbitrarily bad (i) even with only a few outliers in the dataset; or (ii) even if the medium-sized tasks are slightly smaller with $o(k^{1/2})$ examples each. We introduce a spectral approach that is simultaneously robust under both scenarios. To this end, we first design a novel outlier-robust principal component analysis algorithm that achieves an optimal accuracy. This is followed by a sum-of-squares algorithm to exploit the information from higher order moments. Together, this approach is robust against outliers and achieves a graceful statistical trade-off; the lack of $\Omega(k^{1/2})$-size tasks can be compensated for with smaller tasks, which can now be as small as $O(\log k)$.

Meta-learning for mixed linear regression

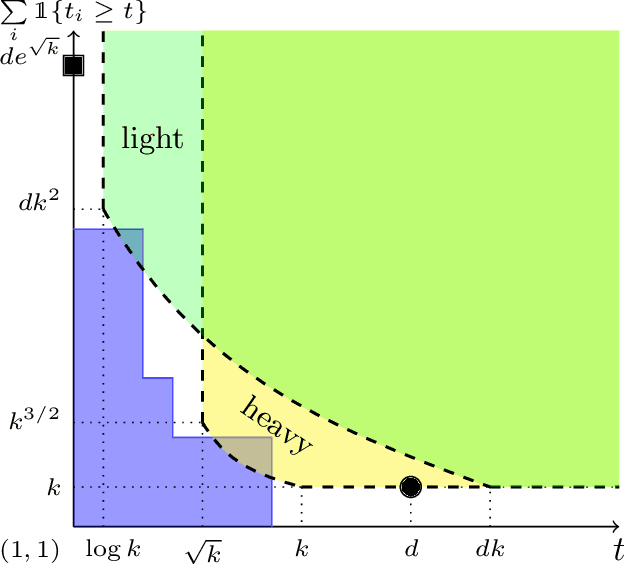
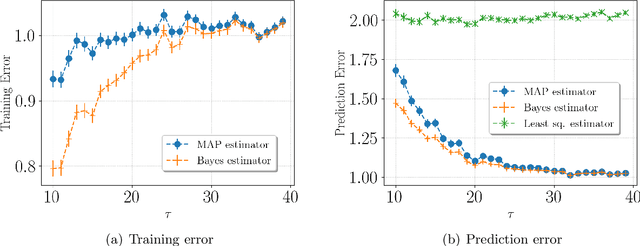
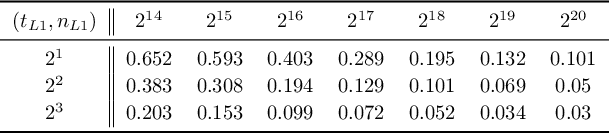
In modern supervised learning, there are a large number of tasks, but many of them are associated with only a small amount of labeled data. These include data from medical image processing and robotic interaction. Even though each individual task cannot be meaningfully trained in isolation, one seeks to meta-learn across the tasks from past experiences by exploiting some similarities. We study a fundamental question of interest: When can abundant tasks with small data compensate for lack of tasks with big data? We focus on a canonical scenario where each task is drawn from a mixture of $k$ linear regressions, and identify sufficient conditions for such a graceful exchange to hold; The total number of examples necessary with only small data tasks scales similarly as when big data tasks are available. To this end, we introduce a novel spectral approach and show that we can efficiently utilize small data tasks with the help of $\tilde\Omega(k^{3/2})$ medium data tasks each with $\tilde\Omega(k^{1/2})$ examples.

Sublinear Optimal Policy Value Estimation in Contextual Bandits

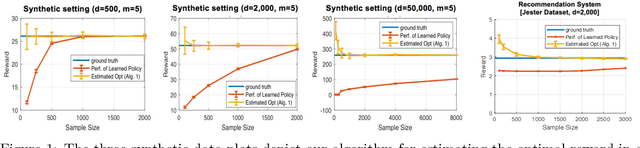
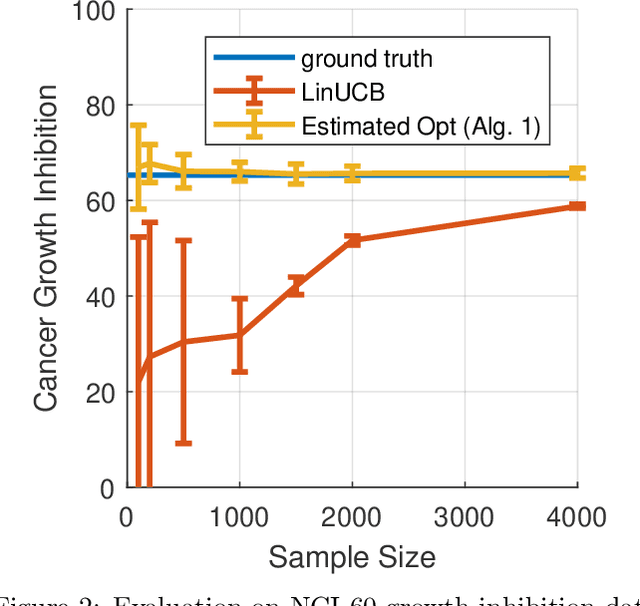
We study the problem of estimating the expected reward of the optimal policy in the stochastic disjoint linear bandit setting. We prove that for certain settings it is possible to obtain an accurate estimate of the optimal policy value even with a number of samples that is sublinear in the number that would be required to \emph{find} a policy that realizes a value close to this optima. We establish nearly matching information theoretic lower bounds, showing that our algorithm achieves near optimal estimation error. Finally, we demonstrate the effectiveness of our algorithm on joke recommendation and cancer inhibition dosage selection problems using real datasets.