Nonparametric mixture MLEs under Gaussian-smoothed optimal transport distance

The Gaussian-smoothed optimal transport (GOT) framework, pioneered in Goldfeld et al. (2020) and followed up by a series of subsequent papers, has quickly caught attention among researchers in statistics, machine learning, information theory, and related fields. One key observation made therein is that, by adapting to the GOT framework instead of its unsmoothed counterpart, the curse of dimensionality for using the empirical measure to approximate the true data generating distribution can be lifted. The current paper shows that a related observation applies to the estimation of nonparametric mixing distributions in discrete exponential family models, where under the GOT cost the estimation accuracy of the nonparametric MLE can be accelerated to a polynomial rate. This is in sharp contrast to the classical sub-polynomial rates based on unsmoothed metrics, which cannot be improved from an information-theoretical perspective. A key step in our analysis is the establishment of a new Jackson-type approximation bound of Gaussian-convoluted Lipschitz functions. This insight bridges existing techniques of analyzing the nonparametric MLEs and the new GOT framework.

Fisher-Pitman permutation tests based on nonparametric Poisson mixtures with application to single cell genomics

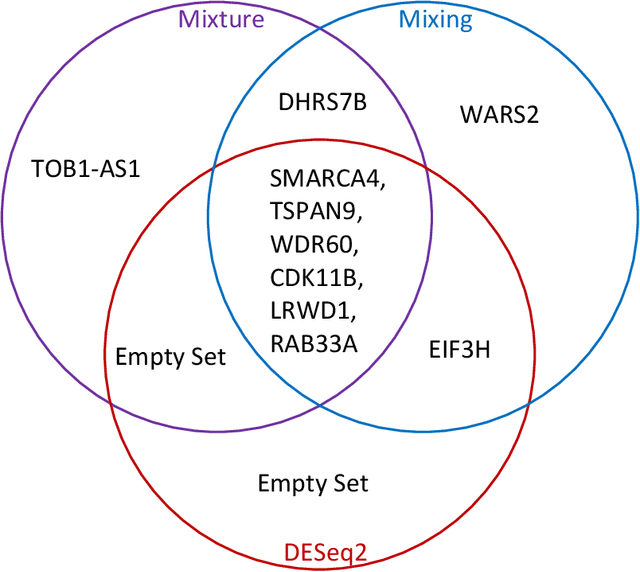
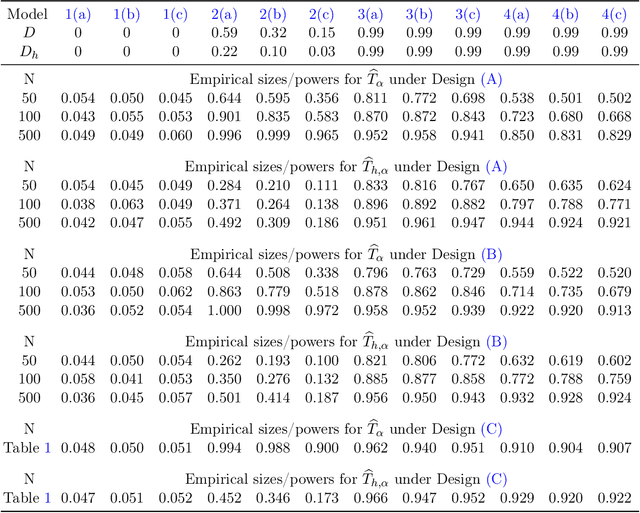
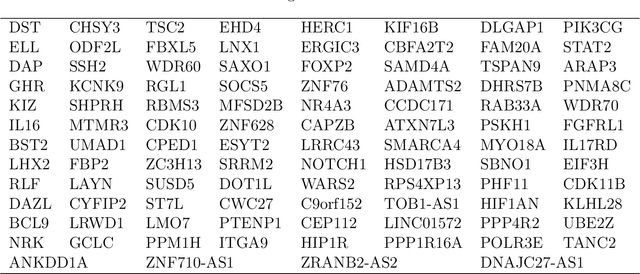
This paper investigates the theoretical and empirical performance of Fisher-Pitman-type permutation tests for assessing the equality of unknown Poisson mixture distributions. Building on nonparametric maximum likelihood estimators (NPMLEs) of the mixing distribution, these tests are theoretically shown to be able to adapt to complicated unspecified structures of count data and also consistent against their corresponding ANOVA-type alternatives; the latter is a result in parallel to classic claims made by Robinson (Robinson, 1973). The studied methods are then applied to a single-cell RNA-seq data obtained from different cell types from brain samples of autism subjects and healthy controls; empirically, they unveil genes that are differentially expressed between autism and control subjects yet are missed using common tests. For justifying their use, rate optimality of NPMLEs is also established in settings similar to nonparametric Gaussian (Wu and Yang, 2020a) and binomial mixtures (Tian et al., 2017; Vinayak et al., 2019).