EVOLvE: Evaluating and Optimizing LLMs For Exploration

Despite their success in many domains, large language models (LLMs) remain under-studied in scenarios requiring optimal decision-making under uncertainty. This is crucial as many real-world applications, ranging from personalized recommendations to healthcare interventions, demand that LLMs not only predict but also actively learn to make optimal decisions through exploration. In this work, we measure LLMs' (in)ability to make optimal decisions in bandits, a state-less reinforcement learning setting relevant to many applications. We develop a comprehensive suite of environments, including both context-free and contextual bandits with varying task difficulties, to benchmark LLMs' performance. Motivated by the existence of optimal exploration algorithms, we propose efficient ways to integrate this algorithmic knowledge into LLMs: by providing explicit algorithm-guided support during inference; and through algorithm distillation via in-context demonstrations and fine-tuning, using synthetic data generated from these algorithms. Impressively, these techniques allow us to achieve superior exploration performance with smaller models, surpassing larger models on various tasks. We conducted an extensive ablation study to shed light on various factors, such as task difficulty and data representation, that influence the efficiency of LLM exploration. Additionally, we conduct a rigorous analysis of the LLM's exploration efficiency using the concept of regret, linking its ability to explore to the model size and underlying algorithm.

Experiment Planning with Function Approximation

We study the problem of experiment planning with function approximation in contextual bandit problems. In settings where there is a significant overhead to deploying adaptive algorithms -- for example, when the execution of the data collection policies is required to be distributed, or a human in the loop is needed to implement these policies -- producing in advance a set of policies for data collection is paramount. We study the setting where a large dataset of contexts but not rewards is available and may be used by the learner to design an effective data collection strategy. Although when rewards are linear this problem has been well studied, results are still missing for more complex reward models. In this work we propose two experiment planning strategies compatible with function approximation. The first is an eluder planning and sampling procedure that can recover optimality guarantees depending on the eluder dimension of the reward function class. For the second, we show that a uniform sampler achieves competitive optimality rates in the setting where the number of actions is small. We finalize our results introducing a statistical gap fleshing out the fundamental differences between planning and adaptive learning and provide results for planning with model selection.

Supervised Pretraining Can Learn In-Context Reinforcement Learning

Large transformer models trained on diverse datasets have shown a remarkable ability to learn in-context, achieving high few-shot performance on tasks they were not explicitly trained to solve. In this paper, we study the in-context learning capabilities of transformers in decision-making problems, i.e., reinforcement learning (RL) for bandits and Markov decision processes. To do so, we introduce and study Decision-Pretrained Transformer (DPT), a supervised pretraining method where the transformer predicts an optimal action given a query state and an in-context dataset of interactions, across a diverse set of tasks. This procedure, while simple, produces a model with several surprising capabilities. We find that the pretrained transformer can be used to solve a range of RL problems in-context, exhibiting both exploration online and conservatism offline, despite not being explicitly trained to do so. The model also generalizes beyond the pretraining distribution to new tasks and automatically adapts its decision-making strategies to unknown structure. Theoretically, we show DPT can be viewed as an efficient implementation of Bayesian posterior sampling, a provably sample-efficient RL algorithm. We further leverage this connection to provide guarantees on the regret of the in-context algorithm yielded by DPT, and prove that it can learn faster than algorithms used to generate the pretraining data. These results suggest a promising yet simple path towards instilling strong in-context decision-making abilities in transformers.

Estimating Optimal Policy Value in General Linear Contextual Bandits

In many bandit problems, the maximal reward achievable by a policy is often unknown in advance. We consider the problem of estimating the optimal policy value in the sublinear data regime before the optimal policy is even learnable. We refer to this as $V^*$ estimation. It was recently shown that fast $V^*$ estimation is possible but only in disjoint linear bandits with Gaussian covariates. Whether this is possible for more realistic context distributions has remained an open and important question for tasks such as model selection. In this paper, we first provide lower bounds showing that this general problem is hard. However, under stronger assumptions, we give an algorithm and analysis proving that $\widetilde{\mathcal{O}}(\sqrt{d})$ sublinear estimation of $V^*$ is indeed information-theoretically possible, where $d$ is the dimension. We then present a more practical, computationally efficient algorithm that estimates a problem-dependent upper bound on $V^*$ that holds for general distributions and is tight when the context distribution is Gaussian. We prove our algorithm requires only $\widetilde{\mathcal{O}}(\sqrt{d})$ samples to estimate the upper bound. We use this upper bound and the estimator to obtain novel and improved guarantees for several applications in bandit model selection and testing for treatment effects.

Learning in POMDPs is Sample-Efficient with Hindsight Observability

POMDPs capture a broad class of decision making problems, but hardness results suggest that learning is intractable even in simple settings due to the inherent partial observability. However, in many realistic problems, more information is either revealed or can be computed during some point of the learning process. Motivated by diverse applications ranging from robotics to data center scheduling, we formulate a Hindsight Observable Markov Decision Process (HOMDP) as a POMDP where the latent states are revealed to the learner in hindsight and only during training. We introduce new algorithms for the tabular and function approximation settings that are provably sample-efficient with hindsight observability, even in POMDPs that would otherwise be statistically intractable. We give a lower bound showing that the tabular algorithm is optimal in its dependence on latent state and observation cardinalities.

Oracle Inequalities for Model Selection in Offline Reinforcement Learning

In offline reinforcement learning (RL), a learner leverages prior logged data to learn a good policy without interacting with the environment. A major challenge in applying such methods in practice is the lack of both theoretically principled and practical tools for model selection and evaluation. To address this, we study the problem of model selection in offline RL with value function approximation. The learner is given a nested sequence of model classes to minimize squared Bellman error and must select among these to achieve a balance between approximation and estimation error of the classes. We propose the first model selection algorithm for offline RL that achieves minimax rate-optimal oracle inequalities up to logarithmic factors. The algorithm, ModBE, takes as input a collection of candidate model classes and a generic base offline RL algorithm. By successively eliminating model classes using a novel one-sided generalization test, ModBE returns a policy with regret scaling with the complexity of the minimally complete model class. In addition to its theoretical guarantees, it is conceptually simple and computationally efficient, amounting to solving a series of square loss regression problems and then comparing relative square loss between classes. We conclude with several numerical simulations showing it is capable of reliably selecting a good model class.

Model Selection in Batch Policy Optimization

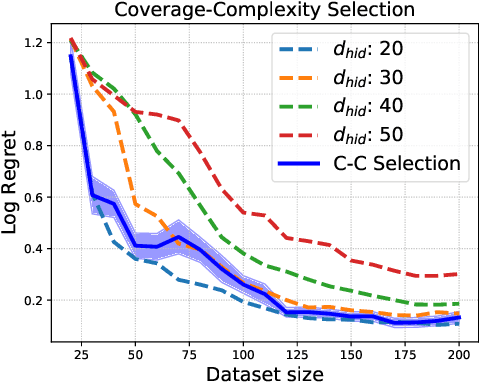
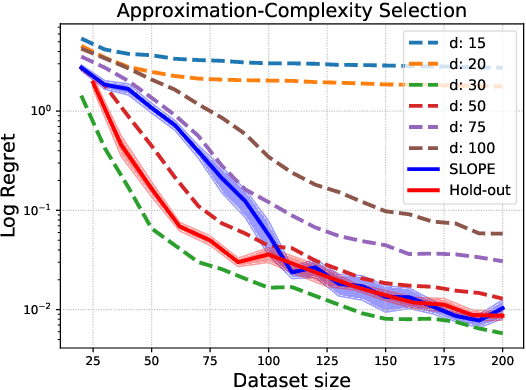
We study the problem of model selection in batch policy optimization: given a fixed, partial-feedback dataset and $M$ model classes, learn a policy with performance that is competitive with the policy derived from the best model class. We formalize the problem in the contextual bandit setting with linear model classes by identifying three sources of error that any model selection algorithm should optimally trade-off in order to be competitive: (1) approximation error, (2) statistical complexity, and (3) coverage. The first two sources are common in model selection for supervised learning, where optimally trading-off these properties is well-studied. In contrast, the third source is unique to batch policy optimization and is due to dataset shift inherent to the setting. We first show that no batch policy optimization algorithm can achieve a guarantee addressing all three simultaneously, revealing a stark contrast between difficulties in batch policy optimization and the positive results available in supervised learning. Despite this negative result, we show that relaxing any one of the three error sources enables the design of algorithms achieving near-oracle inequalities for the remaining two. We conclude with experiments demonstrating the efficacy of these algorithms.

Online Model Selection for Reinforcement Learning with Function Approximation

Deep reinforcement learning has achieved impressive successes yet often requires a very large amount of interaction data. This result is perhaps unsurprising, as using complicated function approximation often requires more data to fit, and early theoretical results on linear Markov decision processes provide regret bounds that scale with the dimension of the linear approximation. Ideally, we would like to automatically identify the minimal dimension of the approximation that is sufficient to encode an optimal policy. Towards this end, we consider the problem of model selection in RL with function approximation, given a set of candidate RL algorithms with known regret guarantees. The learner's goal is to adapt to the complexity of the optimal algorithm without knowing it \textit{a priori}. We present a meta-algorithm that successively rejects increasingly complex models using a simple statistical test. Given at least one candidate that satisfies realizability, we prove the meta-algorithm adapts to the optimal complexity with $\tilde{O}(L^{5/6} T^{2/3})$ regret compared to the optimal candidate's $\tilde{O}(\sqrt T)$ regret, where $T$ is the number of episodes and $L$ is the number of algorithms. The dimension and horizon dependencies remain optimal with respect to the best candidate, and our meta-algorithmic approach is flexible to incorporate multiple candidate algorithms and models. Finally, we show that the meta-algorithm automatically admits significantly improved instance-dependent regret bounds that depend on the gaps between the maximal values attainable by the candidates.

Accelerated Message Passing for Entropy-Regularized MAP Inference

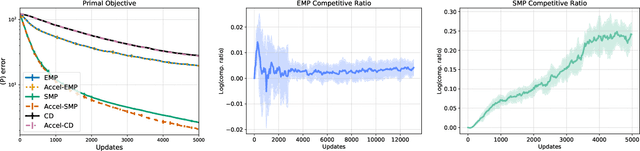
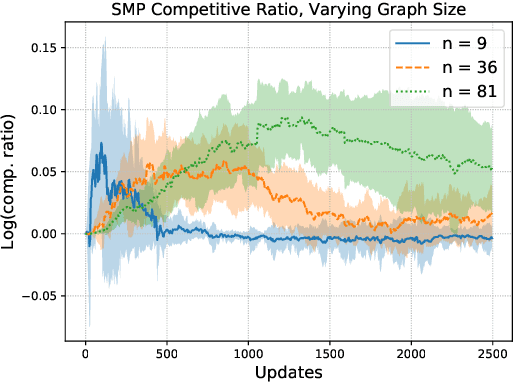
Maximum a posteriori (MAP) inference in discrete-valued Markov random fields is a fundamental problem in machine learning that involves identifying the most likely configuration of random variables given a distribution. Due to the difficulty of this combinatorial problem, linear programming (LP) relaxations are commonly used to derive specialized message passing algorithms that are often interpreted as coordinate descent on the dual LP. To achieve more desirable computational properties, a number of methods regularize the LP with an entropy term, leading to a class of smooth message passing algorithms with convergence guarantees. In this paper, we present randomized methods for accelerating these algorithms by leveraging techniques that underlie classical accelerated gradient methods. The proposed algorithms incorporate the familiar steps of standard smooth message passing algorithms, which can be viewed as coordinate minimization steps. We show that these accelerated variants achieve faster rates for finding $\epsilon$-optimal points of the unregularized problem, and, when the LP is tight, we prove that the proposed algorithms recover the true MAP solution in fewer iterations than standard message passing algorithms.

Approximate Sherali-Adams Relaxations for MAP Inference via Entropy Regularization

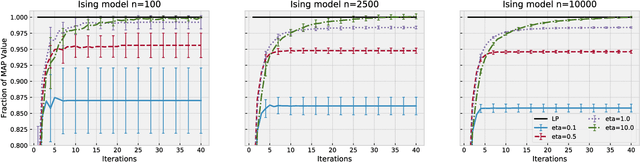
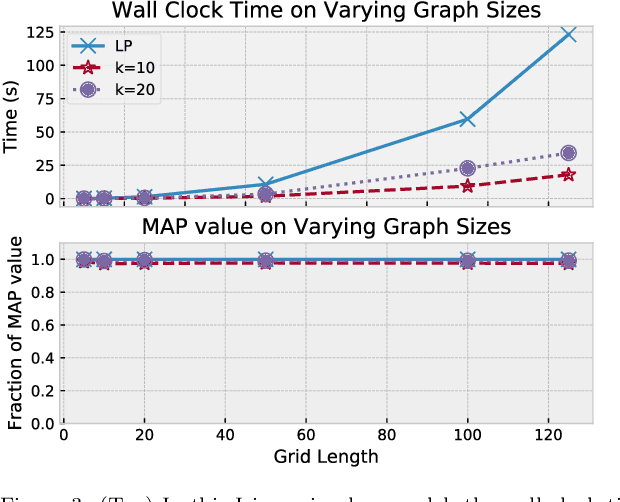
Maximum a posteriori (MAP) inference is a fundamental computational paradigm for statistical inference. In the setting of graphical models, MAP inference entails solving a combinatorial optimization problem to find the most likely configuration of the discrete-valued model. Linear programming (LP) relaxations in the Sherali-Adams hierarchy are widely used to attempt to solve this problem. We leverage recent work in entropy-regularized linear programming to propose an iterative projection algorithm (SMPLP) for large scale MAP inference that is guaranteed to converge to a near-optimal solution to the relaxation. With an appropriately chosen regularization constant, we show the resulting rounded solution solves the exact MAP problem whenever the LP is tight. We further provide theoretical guarantees on the number of iterations sufficient to achieve $\epsilon$-close solutions. Finally, we show in practice that SMPLP is competitive for solving Sherali-Adams relaxations.