Multi-Modal Forecaster: Jointly Predicting Time Series and Textual Data

Current forecasting approaches are largely unimodal and ignore the rich textual data that often accompany the time series due to lack of well-curated multimodal benchmark dataset. In this work, we develop TimeText Corpus (TTC), a carefully curated, time-aligned text and time dataset for multimodal forecasting. Our dataset is composed of sequences of numbers and text aligned to timestamps, and includes data from two different domains: climate science and healthcare. Our data is a significant contribution to the rare selection of available multimodal datasets. We also propose the Hybrid Multi-Modal Forecaster (Hybrid-MMF), a multimodal LLM that jointly forecasts both text and time series data using shared embeddings. However, contrary to our expectations, our Hybrid-MMF model does not outperform existing baselines in our experiments. This negative result highlights the challenges inherent in multimodal forecasting. Our code and data are available at https://github.com/Rose-STL-Lab/Multimodal_ Forecasting.

In-Context Fine-Tuning for Time-Series Foundation Models

Motivated by the recent success of time-series foundation models for zero-shot forecasting, we present a methodology for $\textit{in-context fine-tuning}$ of a time-series foundation model. In particular, we design a pretrained foundation model that can be prompted (at inference time) with multiple time-series examples, in order to forecast a target time-series into the future. Our foundation model is specifically trained to utilize examples from multiple related time-series in its context window (in addition to the history of the target time-series) to help it adapt to the specific distribution of the target domain at inference time. We show that such a foundation model that uses in-context examples at inference time can obtain much better performance on popular forecasting benchmarks compared to supervised deep learning methods, statistical models, as well as other time-series foundation models. Interestingly, our in-context fine-tuning approach even rivals the performance of a foundation model that is explicitly fine-tuned on the target domain.

Transformers can optimally learn regression mixture models

Mixture models arise in many regression problems, but most methods have seen limited adoption partly due to these algorithms' highly-tailored and model-specific nature. On the other hand, transformers are flexible, neural sequence models that present the intriguing possibility of providing general-purpose prediction methods, even in this mixture setting. In this work, we investigate the hypothesis that transformers can learn an optimal predictor for mixtures of regressions. We construct a generative process for a mixture of linear regressions for which the decision-theoretic optimal procedure is given by data-driven exponential weights on a finite set of parameters. We observe that transformers achieve low mean-squared error on data generated via this process. By probing the transformer's output at inference time, we also show that transformers typically make predictions that are close to the optimal predictor. Our experiments also demonstrate that transformers can learn mixtures of regressions in a sample-efficient fashion and are somewhat robust to distribution shifts. We complement our experimental observations by proving constructively that the decision-theoretic optimal procedure is indeed implementable by a transformer.

A decoder-only foundation model for time-series forecasting

Motivated by recent advances in large language models for Natural Language Processing (NLP), we design a time-series foundation model for forecasting whose out-of-the-box zero-shot performance on a variety of public datasets comes close to the accuracy of state-of-the-art supervised forecasting models for each individual dataset. Our model is based on pretraining a patched-decoder style attention model on a large time-series corpus, and can work well across different forecasting history lengths, prediction lengths and temporal granularities.

Linear Regression using Heterogeneous Data Batches

In many learning applications, data are collected from multiple sources, each providing a \emph{batch} of samples that by itself is insufficient to learn its input-output relationship. A common approach assumes that the sources fall in one of several unknown subgroups, each with an unknown input distribution and input-output relationship. We consider one of this setup's most fundamental and important manifestations where the output is a noisy linear combination of the inputs, and there are $k$ subgroups, each with its own regression vector. Prior work~\cite{kong2020meta} showed that with abundant small-batches, the regression vectors can be learned with only few, $\tilde\Omega( k^{3/2})$, batches of medium-size with $\tilde\Omega(\sqrt k)$ samples each. However, the paper requires that the input distribution for all $k$ subgroups be isotropic Gaussian, and states that removing this assumption is an ``interesting and challenging problem". We propose a novel gradient-based algorithm that improves on the existing results in several ways. It extends the applicability of the algorithm by: (1) allowing the subgroups' underlying input distributions to be different, unknown, and heavy-tailed; (2) recovering all subgroups followed by a significant proportion of batches even for infinite $k$; (3) removing the separation requirement between the regression vectors; (4) reducing the number of batches and allowing smaller batch sizes.

Long-term Forecasting with TiDE: Time-series Dense Encoder

Recent work has shown that simple linear models can outperform several Transformer based approaches in long term time-series forecasting. Motivated by this, we propose a Multi-layer Perceptron (MLP) based encoder-decoder model, Time-series Dense Encoder (TiDE), for long-term time-series forecasting that enjoys the simplicity and speed of linear models while also being able to handle covariates and non-linear dependencies. Theoretically, we prove that the simplest linear analogue of our model can achieve near optimal error rate for linear dynamical systems (LDS) under some assumptions. Empirically, we show that our method can match or outperform prior approaches on popular long-term time-series forecasting benchmarks while being 5-10x faster than the best Transformer based model.

Efficient List-Decodable Regression using Batches

We begin the study of list-decodable linear regression using batches. In this setting only an $\alpha \in (0,1]$ fraction of the batches are genuine. Each genuine batch contains $\ge n$ i.i.d. samples from a common unknown distribution and the remaining batches may contain arbitrary or even adversarial samples. We derive a polynomial time algorithm that for any $n\ge \tilde \Omega(1/\alpha)$ returns a list of size $\mathcal O(1/\alpha^2)$ such that one of the items in the list is close to the true regression parameter. The algorithm requires only $\tilde{\mathcal{O}}(d/\alpha^2)$ genuine batches and works under fairly general assumptions on the distribution. The results demonstrate the utility of batch structure, which allows for the first polynomial time algorithm for list-decodable regression, which may be impossible for the non-batch setting, as suggested by a recent SQ lower bound \cite{diakonikolas2021statistical} for the non-batch setting.

Trimmed Maximum Likelihood Estimation for Robust Learning in Generalized Linear Models

We study the problem of learning generalized linear models under adversarial corruptions. We analyze a classical heuristic called the iterative trimmed maximum likelihood estimator which is known to be effective against label corruptions in practice. Under label corruptions, we prove that this simple estimator achieves minimax near-optimal risk on a wide range of generalized linear models, including Gaussian regression, Poisson regression and Binomial regression. Finally, we extend the estimator to the more challenging setting of label and covariate corruptions and demonstrate its robustness and optimality in that setting as well.

A Top-Down Approach to Hierarchically Coherent Probabilistic Forecasting

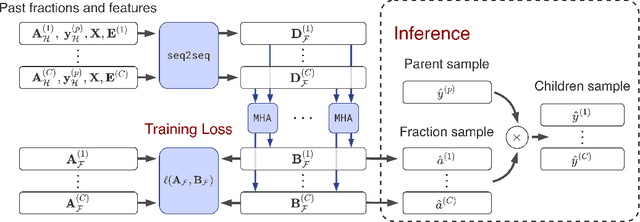
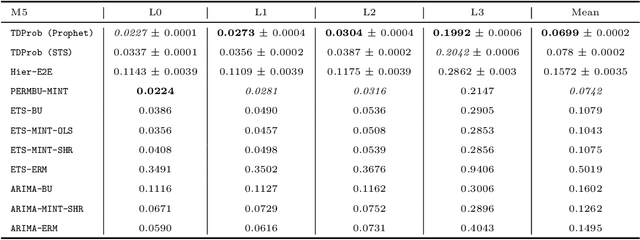
Hierarchical forecasting is a key problem in many practical multivariate forecasting applications - the goal is to obtain coherent predictions for a large number of correlated time series that are arranged in a pre-specified tree hierarchy. In this paper, we present a probabilistic top-down approach to hierarchical forecasting that uses a novel attention-based RNN model to learn the distribution of the proportions according to which each parent prediction is split among its children nodes at any point in time. These probabilistic proportions are then coupled with an independent univariate probabilistic forecasting model (such as Prophet or STS) for the root time series. The resulting forecasts are computed in a top-down fashion and are naturally coherent, and also support probabilistic predictions over all time series in the hierarchy. We provide theoretical justification for the superiority of our top-down approach compared to traditional bottom-up hierarchical modeling. Finally, we experiment on three public datasets and demonstrate significantly improved probabilistic forecasts, compared to state-of-the-art probabilistic hierarchical models.

Leveraging Initial Hints for Free in Stochastic Linear Bandits

We study the setting of optimizing with bandit feedback with additional prior knowledge provided to the learner in the form of an initial hint of the optimal action. We present a novel algorithm for stochastic linear bandits that uses this hint to improve its regret to $\tilde O(\sqrt{T})$ when the hint is accurate, while maintaining a minimax-optimal $\tilde O(d\sqrt{T})$ regret independent of the quality of the hint. Furthermore, we provide a Pareto frontier of tight tradeoffs between best-case and worst-case regret, with matching lower bounds. Perhaps surprisingly, our work shows that leveraging a hint shows provable gains without sacrificing worst-case performance, implying that our algorithm adapts to the quality of the hint for free. We also provide an extension of our algorithm to the case of $m$ initial hints, showing that we can achieve a $\tilde O(m^{2/3}\sqrt{T})$ regret.